Géométrie Euclidienne

William BOURGES © 2023

Sommaire

Géométrie Euclidienne

Axiomes d'incidence

On se place dans un ensemble IP dont les éléments sont appelés points, et la réunion de certains points sont appelés des droites.
Cette ensemble IP vérifie les axiomes suivants :

Axiome I1 : Etant donné une droite, il existe au moins deux points distincts sur cette droite.

Axiome I2 : Etant donné deux points A et B distincts, il existe une unique droite passant par A et B.

Définition : On dit que trois points sont alignés, il existe une droite passant par ces trois points.

Axiome I3 : Il existe trois points non alignés.

Définition : On note (AB) ou (BA) l'unique droite passant par les deux points distincts A et B.

Définition : Deux droites sont parallèles si elles n’ont aucun point en commun ou si elles sont confondues.

Propriété PI1 (I1, I2) : Si deux droites distinctes sont non parallèles, alors elles ont un unique point en commun.

Démonstration de PI1 :
Soient (d) et (d’) deux droites distinctes et non parallèles.
Donc par définition, elles ont au moins un point A en commun.
D'après l'axiome I1, il existe un autre point sur (d) et un autre point sur(d').
Si elles avaient un autre point B en commun, alors d’après l’axiome I2, les droites (d) et (d’) seraient confondues.
Ce qui absurde, car (d) et (d’) sont distinctes.
Donc (d) et (d’) ont un unique point en commun.
CQFD

Propriété PI2 (I2, I3) : Pour tout point, il existe au moins une droite ne passant pas par ce point.

Démonstration de PI2 :
Soit M un point.
D’après l’axiome I3, il existe trois points A, B et C distincts et non alignés.

1^er Cas : Si M∉(AB).
Alors la droite (AB) convient.

2^ième Cas : Si M∈(AB) et si M ≠ A.
Alors la droite (AC) convient.
Car si (AC) passe par M, alors (AB) et (AC) ont les points A et M en commun, et donc d’après l’axiome I2, les points A, B et C sont alignés. Ce qui est contradictoire.

3^ième Cas : Si M = A
Alors la droite (BC) convient, car les points A, B et C ne sont pas alignés.
CQFD

Propriété PI3 (I3) : Pour toute droite, il existe au moins un point ne lui appartenant pas.

Démonstration de PI3 :
Soit (d) une droite.
D’après l’axiome I3, il existe trois points A, B et C distincts et non alignés.
Donc un des trois points ne peut appartenir à (d).
CQFD

Propriété PI4 (I2, I3) : Pour tout point, il existe au moins deux droites distinctes auxquelles ce point appartient.

Démonstration de PI4 :
Soit M un point,d’après l’axiome I3, il existe trois points A, B et C distincts et non alignés.
Donc M ne peut être égal à la fois, aux points A, B et C.

1^er Cas : A = M. De même si B = M ou C = M.
Donc le point M appartient aux droites (BM) et (CM).
Les droites (BM) et (CM) sont distinctes car sinon d'après l'axiome I2, les points A, B et C seraient alignés.

2^ième Cas : Si M est distinct des points A, B et C.
Les droites (AM), (BM) et (CM) ne peuvent être la même droite car sinon les points A, B et C seraient alignés. Donc le point M appartient à au moins deux droites distinctes.
CQFD

Axiomes d'ordre

L’ensemble IP est muni d’une relation ternaire * telle que si A, B et C sont trois points, on note A*B*C le fait que A, B et C sont distincts, alignés, et B est entre A et C.

Définition : Si A et B sont deux points distincts, alors on appelle segment [AB] ou [BA] l’ensemble formé par les points A et B, et les points M tel que A*M*B. Le point A, peut-être vu comme le segment [AA].

Définition : Si A et B sont deux points distincts. On appelle demi-droite [AB) ou (BA], l’ensemble formé par les points A et B, et les points M tel que A*M*B ou A*B*M.

Axiome O1 : Si A*B*C alors C*B*A.

Axiome O2 : Etant donné deux points distincts B et D, il existe des points A, C, E appartenant à la droite (BD) tels que A*B*D, B*C*D et B*D*E.

Axiome O3 : Si A, B, C sont trois points distincts appartenant à la même droite, alors un et un seul est entre les deux autres.

Définition : Soient (d) une droite, et A et B deux points distincts n’appartenant pas à (d).
(1) Si [AB]⋂(d)=∅, alors on dit que les points A et B sont du même côté de (d).
(2) Si [AB]⋂(d)≠∅, alors on dit que les points A et B sont de part et d’autre de (d).
(3) Dans le cas où A=B, on dit que les points A et B sont du même côté de (d).

Axiome O4 : Pour toute droite (d), et tout triplet de points A, B, C non situés sur (d) :
(1) Si A et B sont d'un même côté de (d), et B et C aussi, alors A et C sont du même côté de (d).
(2) Si A et B sont de part et d'autre de (d), et B et C aussi, alors A et C sont d'un même côté de (d).

Propriété PO1 (O3) : Si A et B deux points distincts, alors [AB)⋂[BA) = [AB] et [AB)⋃[BA) = (AB).

Démonstration de PO1 :
Soient A et B deux points distincts.
M∈[AB)⋂[BA)
<=> M∈[AB) et M∈[BA)
<=> (M= A ou M= B ou A*M*B ou A*B*M) et (M=A ou M = B ou A*M*B ou B*A*M)
<=> M=A ou M = B ou A*M*B d’après l’axiome O3 
<=> M∈[AB]

M∈[AB)⋃[BA)
<=> M∈[AB) ou M∈[BA)
<=> (M= A ou M= B ou A*M*B ou A*B*M) ou (M= A ou M = B ou A*M*B ou B*A*M)
<=> M=A ou M=B ou A*M*B ou A*B*M ou B*A*M
<=> M∈(AB)
CQFD

Définition : Soient A, B et C trois points distincts. Si B*A*C alors on dit les demi-droites [AB) et [AC) sont opposées.

Propriété PO2 (O2, O3) :
(1) Deux demi-droites opposées sont distinctes.
(2) Toute demi-droite admet une demi-droite opposée.

Démonstration de PO2 :
(1) Soient A, B et C trois points distincts tel que B*A*C. Montrons que les demi-droites [AB) et [AC) opposées sont distinctes.
Supposons que C∈[AB)
Donc C=A ou C= B ou A*C*B ou A*B*C
Or A, B et C trois points distincts tels que B*A*C
Donc d’après l’axiome O3, ceci est absurde.
Donc les demi-droites [AB) et [AC) sont opposées.
CQFD

(2) Soient A et B deux points distincts.
D’après l’axiome O2, il existe un point C tel que B*A*C.
Donc la demi-droite [AB), admet [AC) comme demi-droite opposé.
CQFD

Définition : On appelle demi-plan (P_A,d) défini par la droite (d) et un point A n’appartenant pas à (d), l’ensemble des points qui sont du même côté que le point A par rapport à (d).

Propriété PO3 (O2,O4,PI1,PI3 ) :
(1) Toute droite (d) détermine deux demi-plans qui n’ont aucun point commun, et tout point n’appartenant pas à (d) est dans un de ces demi-plans.
(2) Si A et B sont de part et d’autre de (d), alors (d) détermine les demi-plans (P_A,d) et (P_B,d).

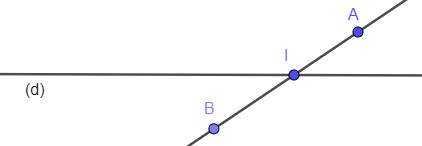
Démonstration de PO3 :
Soit (d) une droite.
D’après la propriété PI3, il existe au moins un point A n’appartenant pas à (d).
A et (d) définissent le demi-plan (P_A,d)
Soit I un point de (d).
I ≠A car A(d)
Donc la droite (AI) est bien définie.
D’après l’axiome O2, il existe un point B sur (AI) tel que A*I*B.
Donc les points A et B sont de part et d’autre de (d), et A ≠ B.
(AI) et (d) sont deux droites distinctes et non parallèles car A(d) et I∈(d)
Donc d’après la propriété PI1, (AI) et (d) ont un unique point en commun, soit I.
Si B∈(d) comme B∈(AI), alors B = I.
Ce qui est contradictoire car A*I*B, soit en particulier B≠I.
Donc B(d)
Donc B et (d) définissent le demi-plan (P_B,d)

Soit M∈(P_A,d)
Donc A et M sont du même côté par rapport à (d)
Si B =M alors A et B sont du même côté par rapport à (d) et A ≠B.
Ce qui est contradictoire avec les points A et B sont de part et d’autre de (d), et A ≠ B.
Donc B≠M.
Si B et M sont du même côté par rapport à (d), alors d’après Axiome O4(1), A et B sont du même côté.
Ce qui est contradictoire car les points A et B sont de part et d’autre de (d), et A≠B.
Donc B et M sont de part et d’autre par rapport à (d), et B≠M.
Donc M(P_B,d).
De même, si M∈(P_B,d), alors M(P_A,d).
Donc (P_A,d) et (P_B,d) n’ont aucun point commun.

Reste à démontrer que tout point C n’appartenant pas à (d), appartient à (P_A,d) ou à (P_B,d).
1^er Cas : Si C = A
Alors C∈(P_A,d), car A et A sont du même côté par rapport à (d).
2^ième Cas : Si C≠A et [AC]⋂(d)=∅
Alors les points A et C sont du même côté de (d).
Donc C∈(P_A,d).
3^ième Cas : Si C≠A et [AC]⋂(d)≠∅
Donc A et C sont de part et d’autre par rapport à (d)
Mais comme les points A et B sont de part et d’autre de (d), d’après l’axiome O4(2), les points A et C sont du même côté de (d).
Donc C∈(P_B,d).
CQFD

Propriété PO4_Pasch(O4, PO3) ou Postulat de Pasch : Si ABC est un triangle, et (d) une droite coupant le segment [AB], alors (d) coupe aussi [AC] ou [BC].

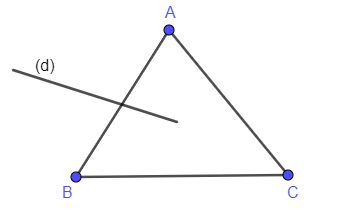
Démonstration de PO4_Pasch :
1^er Cas : Si C∈(d)
Donc (d) coupe aussi [AC] et [BC] en C. 2^ième Cas : Si C(d)
A≠B et [AB]⋂(d)≠∅ donc A et B sont de part et d’autre de (d).
Donc d’après la propriété PO3, C∈(P_A,d) ou C∈(P_B,d)
1^er Sous cas : si C∈(P_A,d)
Donc A et C sont du même côté par rapport à (d).
Si B et C étaient du même côté par rapport à (d), alors d’après axiome O4, A et B seraient du même côté par rapport à (d). Ce qui est contradictoire avec A et B sont de part et d’autre de (d).
Donc B et C sont de part et d’autre de (d).
Donc [BC]⋂(d)≠∅
Donc (d) coupe le segment [BC]
2^ième sous cas : Si C∈(P_B,d)
De même, on démontre que (d) coupe le segment [AC].
CQFD

Propriété PO5 (O3, PI1) : Si (d) une droite, A et B sont deux points tels que A∈(d) et B(d), alors ]AB) ⊂ (P_B,d).

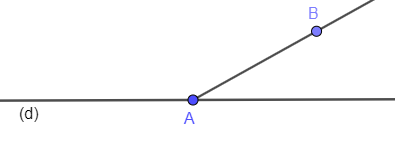
Démonstration de PO5 :
M∈]AB) donc A*M*B ou M=B ou A*B*M
1^er Cas : M=B
Alors [MB]⋂(d)={B}⋂(d)=∅ car B(d).
Donc M et B sont du même côté par rapport à (d).
Donc M∈(P_B,d).
2^ième Cas : Si A*M*B et M≠B
Supposons que [MB]⋂(d)≠∅
Comme A*M*B, alors A, M et B sont distincts et alignés.
Et comme aussi A∈(d), A∈(MB) et B(d), alors d’après la propriété PI1, (MB)⋂(d)={A}
[MB]⋂(d)≠∅
Donc A∈[MB], et A, M et B sont distincts.
Donc M*A*B.
Or A*M*B, ce qui est contradictoire avec l’axiome O3.
Donc [MB]⋂(d)=∅ et M≠B.
Donc M et B sont du même côté par rapport à (d).
Donc M∈(P_B,d).
3^ième Cas : Si A*B*M et M≠B
Supposons que [MB]⋂(d)≠∅
Comme A*B*M, alors A, M et B sont distincts et alignés.
Et comme aussi A∈(d) , A∈(MB) et B(d), alors d’après la propriété PI1, [MB]⋂(d)={A}
[MB]⋂(d)≠∅
Donc A∈[MB], et A, M et B sont distincts.
Donc M*A*B.
Or A*B*M, ce qui est contradictoire avec l’axiome O3.
Donc [MB]⋂(d)=∅ et M≠B.
Donc M et B sont du même côté par rapport à (d).
Donc M∈(P_B,d).
CQFD

Propriété PO6 (I2,O3, PI1, PI3, PO3, PO5) : Si B*A*C, alors (BC)=[AB)⋃[AC) et [AB)⋂[AC)={A}.

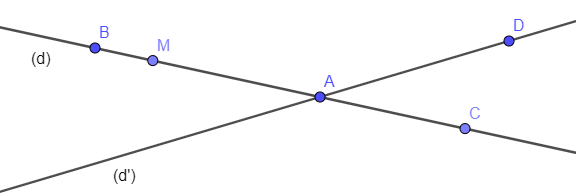
Démonstration de PO6 :
B*A*C donc il existe une droite (d) tels que A, B et C appartiennent à (d).
D’après la propriété PI3, il existe un point D n’appartenant pas à (d).
A≠D, donc notons (d’) la droite (AD)
D(d) donc (d) et (d’) sont distinctes.
A∈(d), A∈(d’) et D(d).
Donc d’après la propriété PI1, (d)⋂(d’)={A}
Si [BC]⋂(d’)=∅, comme A∈(d’), alors A[BC]. Ce qui est contradictoire avec B*A*C.
Donc [BC]⋂(d’)≠∅.
B*A*C donc B≠C.
Donc B et C sont de part et d’autre par rapport à (d’).
Donc d’après la propriété PO3, (d’) détermine les demi-plans (P_B,d’) et (P_C,d’)

Soit M∈(BC)
1^er Cas : Si M=A
A∈[AB)et A∈[AC) donc A∈[AB)⋃[AC) donc M∈[AB)⋃[AC)
2^ième Cas : Si M≠A
(BC)=(d), (d)⋂(d’) ={A}donc M(d’)
Donc d’après la propriété PO3, M∈(P_B,d’) ou M∈(P_C,d’)
1^er sous cas : si M∈(P_B,d’)
Donc M et B sont du même côté par rapport à (d’)
M, A et B appartiennent à (d) donc M=B ou d’après l'axiome O3, M*A*B ou A*M*B ou A*B*M
Si M=B, alors M∈[AB).
Si M≠B et M*A*B, alors M et B sont de part et d’autre de (d’). Ce qui est contradictoire.
Si M≠B et A*M*B, alors M∈[AB], donc M∈[AB).
Si M≠B et A*B*M, alors par définition, M∈[AB).
2^ième sous cas : si M∈(P_C,d’)
De même, on démontre que M∈[AC).
Donc M∈(BC) M∈[AB)⋃[AC)
Donc (BC) ⊂[AB)⋃[AC)
B*A*C donc B, A et C sont distincts et alignés
Donc d’après l'axiome I2, (BC)=(AB)=(AC)
[AB)⊂(AB)=(BC) et [AC)⊂(AC)=(BC) donc [AB)⋃[AC)⊂(BC)
Donc (BC)=[AB)⋃[AC).

Enfin d’après la propriété PO5, ]AB) ⊂ (P_B,d’) et ]AC) ⊂ (P_C,d’)
D’après la propriété PO3, (P_B,d’) ⋂ (P_C,d’) = ∅
Donc ]AB)⋂]AC) = ∅.
Donc [AB)⋂[AC)={A}.
CQFD

Propriété PO7 (I2,O3,O4,PI1,PI3) : Si A*B*C et A*C*D, alors B*C*D et A*B*D.

Démonstration de PO7 :
A*B*C et A*C*D, donc A, B, C et D sont alignés d’après l'axiome I2.
D’après la propriété PI3, il existe un point M n’appartenant pas à (AB).
A*C*D donc A et D sont de part et d’autre de (CM).
Si B et A étaient de part et d’autre de (CM), alors A*C*B ce qui est contradictoire avec A*B*C d’après l'axiome O3.
Donc A et B sont du même côté par rapport à (CM).
Donc B et D sont de part et d’autre de (CM) d’après O4.
Donc d’après la proriété PI1, B*C*D.
A*B*C donc A et C sont de part et d’autre de (BM).
Si C et D étaient de part et d’autre de (BM), alors C*B*D ce qui est contradictoire avec B*C*D d’après l'axiome O3.
B*C*D donc C et D sont du même côté par rapport à (BM).
Donc d’après l'axiome O4, A et D sont de part et d’autre de (BM).
Donc d’après la propriété PI1, A*B*D.
CQFD

Propriété PO8 (I2,O3,O4,PI1,PI3) : Si A*B*C et B*C*D, alors A*B*D et A*C*D.

Démonstration de PO8 :
A*B*C et B*C*D, donc A, B, C et D sont alignés d’après l'axiome I2.
D’après la propriété PI3, il existe un point M n’appartenant pas à (AB).
A*B*C donc A et C sont de part et d’autre de (BM).
Si C et D étaient de part et d’autre de (BM), alors C*B*D ce qui est contradictoire avec B*C*D d’après l'axiome O3.
B*C*D donc C et D sont du même côté par rapport à (BM).
Donc d’après l'axiome O4, A et D sont de part et d’autre de (BM).
Donc d’après la propriété PI1, A*B*D.
Si A et B étaient de part et d’autre de (CM), alors A*C*B ce qui est contradictoire avec A*B*C d’après l'axiome O3.
A*B*C donc A et B sont du même côté par rapport à (CM).
B*C*D donc B et D sont de part et d’autre de (CM).
Donc d’après l'axiome O4, A et D sont de part et d’autre de (CM).
Donc d’après la propriété PI1, A*C*D.
CQFD

Axiomes de congruence

L’ensemble IP est muni d’une relation de congruence sur les segments, notée ≅ .

Axiome C1 : Si A et B sont deux points distincts et A' un point quelconque, pour toute demi-droite [d) d'origine A',alors il existe un point unique B’ de [d) tel que B'≠ A' et [AB] ≅ [A'B'].

Axiome C2 : Si [AB] ≅ [CD] et [AB] ≅ [EF], alors [CD] ≅ [EF]. Tout segment est congru à lui-même.

Axiome C3 : Si A*B*C, A'*B'*C', [AB] ≅ [A'B'], et [BC] ≅ [B'C'], alors [AC] ≅ [A'C'] (addition).

Propriété PC1 (C1,C2,C3,O4,PI1,PI3,PO5):
(1) Si A*B *C, A’*B’*C’, [AB] ≅ [A’B’] et [AC] ≅ [A’C’], alors [BC] ≅ [B’C’] (Soustraction).
(2) Si [AC] ≅ [DF] et un point B tel que A*B*C, alors il existe un unique point E, tel que D*E*F et [AB] ≅ [DE].

Démonstration de PC1 :
(1) Soient A*B *C, A’*B’*C’, [AB] ≅ [A’B’] et [AC] ≅ [A’C’]
D’après l’axiome C1, il existe un point unique C’’ de [B’C’) tel que C’'≠ B' et [BC] ≅ [B'C''].
D’après la propriété PI3, il existe un point M n’appartenant pas à (B’C’).
Donc d’après la propriété PO5, ]B’C’) ⊂ P(C’,(B’M))
C’’est un point de [B’C’) et C’'≠ B' donc C’’∈ P(C’,(B’M))
Donc C’et C’’ sont du même côté par rapport à la droite (B’M)
A’*B’*C’donc A’ et C’sont de part et d’autre de (B’M)
Donc d’après l'axiome O4, A’ et C’’ sont de part et d’autre de (B’M).
Donc d’après la propriété PI1, A’*B’*C’’.
A*B *C, A’*B’*C’’, [AB] ≅ [A’B’] et [BC] ≅ [B’C’’]
Donc d’après l'axiome C3, [AC] ≅ [A'C'’]

A’*B’*C’ donc C’ et B’ sont du même côté par rapport à la droite (A’M).
A’*B’*C’’ donc C’’ et B’ sont du même côté par rapport à la droite (A’M).
Donc d’après l'axiome O4, C’ et C’’ sont du même côté par rapport à la droite (A’M).
A’*B’*C’ et A’*B’*C’’ donc A’, B’, C’ et C’’ sont alignés
Donc C’’∈ [A’C’)
C’’∈ [A’C’) tel que C’'≠ A' et [AC] ≅ [A'C''].
C’ ∈ [A’C’) tel que C'≠ A' et [AC] ≅ [A'C'].
Donc d’après l’unicité de l'axiome C1, C’= C’’
Et donc [BC] ≅ [B'C'].

(2) [AC] ≅ [DF] donc d’après l’axiome C1, il existe un unique point E sur la demi-droite [DF) tel que E≠D et [AB] ≅ [DE].
Il reste à démontrer que D*E*F.
D’après l’axiome C1, il existe F’ tel que D*E*F’ et [EF’] ≅ [BC]
A*B*C, D*E*F’, [AB] ≅ [DE] et [EF’] ≅ [BC] Donc d’après l’axiome C3 on : [DF’] ≅ [AC].
[DF’] ≅ [AC] et [AC] ≅ [DF] donc d’après l’axiome C2, on a : [DF’] ≅ [DF’]
Donc d’après l’axiome C1, on a : F = F’.
D*E*F’ et F = F’ donc D*E*F.
CQFD

L’ensemble IP est muni d’une relation sur les segments, notée < et > telle que : [AB] < [CD] ou [CD] > [AB] si ∃E \ C*E*D et [AB] ≅ [DE].

Propriétés PC2 (C1,C2,O3,PC1,PO7) : Si A et B, C et D, E et F sont des couples de points distincts, alors :
(1) Quels que soient deux segments [AB] et [CD], une seule des trois conditions suivantes est vraie :
[AB] < [CD] ; [AB] ≅ [CD] ; [CD] < [AB].
(2) Si [AB] < [CD] et [CD] ≅ [EF], alors [AB] < [EF].
(3) Si [AB] > [CD] et [CD] ≅ [EF], alors [AB] > [EF].
(4) Si [AB] < [CD] et [CD] < [EF], alors [AB] < [EF].

Démonstration de PC2 :
(1) D'après l'axiome C1, il existe un point E unique sur la demi-droite [AB) telle que A≠E et [AE] ≅ [CD].
1^er Cas : Si E=B,
[AE] ≅ [CD] donc [AB] ≅ [CD].
2^ième Cas : Si E≠B
A≠B, A≠E et B≠E donc d’après l’axiome O3, on a : E*A*B ou A*E*B ou A*B*E
E appartient sur la demi-droite [AB) donc on ne peut avoir E*A*B.
Donc si on a : A*E*B, alors [CD] < [AB].
Et si on a : A*B*E, alors [AB] < [CD].
Les cas E≠B, A*E*B et A*B*E ne pouvant être des cas communs.
Une seule des trois conditions suivantes est vraie : [AB] < [CD] ; [AB] ≅ [CD] ; [CD] < [AB].

(2) D’après le (1), [AB] et [EF], une seule des trois conditions suivantes est vraie : [AB] < [EF] ; [AB] ≅ [EF] ; [EF] < [AB].
1^er cas : si [AB] ≅ [EF]
[AB] ≅ [EF] et [CD] ≅ [EF] donc [AB] ≅ [CD] ce qui est impossible d’après (1) car [AB] < [CD] et une seule des trois conditions suivantes est vraie : [AB] < [CD] ; [AB] ≅ [CD] ; [CD] < [AB].
2^ième Cas : si [EF] < [AB]
[EF] < [AB] donc il existe un unique point B’ tel que A*B’*B et [AB’] ≅ [EF].
[AB] < [CD] donc il existe un unique point C’ tel que C*C’*D et [CC’] ≅ [AB].
[CC’] ≅ [AB’] donc [AB’] ≅ [CC’]
et on a : A*B’*B
D'après la propriété PC1(2), il existe un point C’’ telle que C*C’’*C’ et [CC’’] ≅ [AB’].

C*C’’*C’ et C*C’*D donc d’après la propriété PO7, on a : C*C’’*D.
[CC’’] ≅ [AB’] et [AB’] ≅ [EF] donc d’après l’axiome C2, on a : [CC’’] ≅ [EF].
Donc il existe un point C tel que C*C’’*D et [CC’’] ≅ [EF].
Donc [EF] < [CD]
Ce qui est impossible car [EF] ≅ [CD] et une seule des trois conditions suivantes est vraie : [EF] < [CD] ; [EF] ≅ [CD] ; [EF] < [CD].
3ième Cas : [AB] < [EF]
Ce cas est nécessairement vrai car une seule des trois conditions suivantes est vraie : [AB] < [EF] ; [AB] ≅ [EF] ; [EF] < [AB] et [AB] ≅ [EF] ; [EF] < [AB] sont fausses.

(3)[AB] > [CD] donc il existe un point B’ tel que A*B’*B et [AB’] ≅ [CD].
[AB’] ≅ [CD] et [CD] ≅ [EF] donc d’après l’axiome C2, on a : [AB’] ≅ [EF]
Donc il existe un point B’ tel que A*B’*B et [AB’] ≅ [EF].
Donc [AB] > [EF].
(4) [AB] < [CD] donc il existe un point C' tel que C*C'*D et [CC'] ≅ [AB].
[CD] < [EF] donc il existe un point F' tel que E*F'*F et [EF'] ≅ [CD].
[AB] < [CD] et [CC'] ≅ [AB] donc d’après (3), on a : [CC’] < [CD]
[CC’] < [CD] et [EF'] ≅ [CD] donc d’après (2), on a : [CC’] < [EF’]
[CC’] < [EF’] et [CC'] ≅ [AB] donc d’après (3), on a : [AB] < [EF’]
[AB] < [EF’] donc il existe un point F’' tel que E*F’'*F’ et [EF'’] ≅ [AB].
E*F’'*F’ et E*F'*F donc d’après la propriété PO7, on a : E*F’’*F
Donc il existe un point F’’ tel que E*F’’*F et [EF'’] ≅ [AB].
Donc [AB] < [EF’].
CQFD

Définition : On appelle angle ∠BAC, l’ensemble de deux demi-droites de même origine [AB) et [AC) qui ne sont ni opposées, ni confondues.

L’ensemble IP est muni d’une relation de congruence sur les angles, notée aussi ≅ .

Axiomes C4 : Pour tout angle ∠BAC et toute demi-droite [A'B), il existe une unique demi-droite [A'C') qui soit d'un côté donné de (A'B') et telle que ∠B’A’C’ ≅ ∠BAC.

Axiomes C5 : Si ∠A ≅ ∠B, et ∠B ≅ ∠C, alors ∠A ≅ ∠C. Et tout angle est congru à lui-même.

Définition : On dit que deux triangles ABC et A'B'C' sont congruents si [AB] ≅ [A'B'], [BC] ≅ [B'C'], [AC] ≅ [A'C'], ∠A ≅∠A’, ∠B≅ ∠B’ et ∠C ≅∠C’.

Axiomes C6 : Si deux triangles ont un angle congruent compris entre deux côtés congruents, alors ces deux triangles sont congruents.

Propriétés PC3 (C6) : Si un triangle est isocèle, alors ces angles à sa base sont égaux.

Démonstration de PC3 :
Soit ABC un triangle tel que : [AB] ≅ [AC], montrons que ∠B ≅ ∠C.
∠BAC ≅ ∠CAB, [AB] ≅ [AC] et [AC] ≅ [AB], donc d’après l’axiome C6, on a : les triangles ABC et ACB sont congruents.
Donc ∠B ≅ ∠C. CQFD

Propriété PC4 (C3,C6) :
(1) Les angles supplémentaires d’angles congruents sont congruents.
(2) Les angles opposés par le sommet sont congruents.

Démonstration de PC4 :
(1)

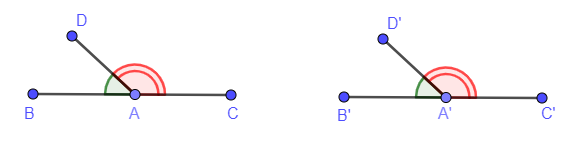
Soient A, B, C, D et A’, B’, C’, D’ tels que B*A*C et B’*A’*C’, et ∠BAD ≅ ∠B’A’D’.
On peut poser aussi, sans restreindre les hypothèses que [AB] ≅ [A'B'], [AC] ≅ [A'C'], [AD] ≅ [A'D'].
[AB] ≅ [A'B'], [AD] ≅ [A'D'], ∠BAD ≅ ∠B’A’D’
Donc d’après l’axiome C6, on a : les triangles BAD et B’A’D’ sont congruents.
Donc [BD] ≅ [B'D'] et ∠ABD ≅ ∠A’B’D’.
[AB] ≅ [A'B'] donc [BA] ≅ [B'A’]
B*A*C et B’*A’*C’, [BA] ≅ [B'A’] et [AC] ≅ [A'C'] donc d’après l’axiome C3, on a : [BC] ≅ [B'C’].
∠ABD ≅ ∠A’B’D’ donc ∠CBD ≅ ∠C’B’D’ car, puisque B*A*C et B’*A’*C’, [BA) et [BC) sont la même demi-droite, de même pour [B’A’) et [B’C’)
[BC] ≅ [B'C’] et [BD] ≅ [B'D'] et ∠CBD ≅ ∠C’B’D’
Donc d’après l’axiome C6, on a : les triangles CBD et C’B’D’ sont congruents.
Donc [CD] ≅ [C'D'] et ∠BCD ≅ ∠B’C’D’.
[AC] ≅ [A'C'] donc [CA] ≅ [C'A'].
∠BCD ≅ ∠B’C’D’ donc ∠ACD ≅ ∠A’C’D’ car, puisque B*A*C et B’*A’*C’, [CA) et [CB) sont la même demi-droite, de même pour [C’A’) et [C’B’)
[CA] ≅ [C'A'] et [CD] ≅ [C'D'] et ∠ACD ≅ ∠A’C’D’
Donc d’après l’axiome C6, on a : les triangles ACD et A’C’D’ sont congruents.
Donc ∠DAC ≅ ∠D’A’C’.
(2)

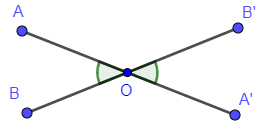
Soient deux angles ∠AOB et ∠A’OB’ tels que A*O*A’ et B’*O*B’.
∠AOB et ∠A’OB’ sont tous les deux supplémentaires à ∠AOB’ donc d’après (1), ils sont congruents.
CQFD

Propriété PC5 () : Si deux droites sont coupées par une troisième droite, et si les angles alternes-internes formés sont congruents, alors les droites sont parallèles.

Démonstration de PC5 :
...

Axiomes de continuité

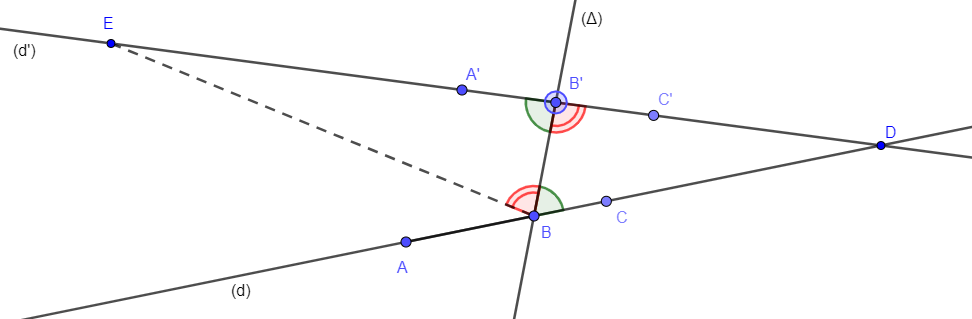Axiome Dkp_segment Dedekind segment ouvert : Si l'ensemble des points de ]AB[ est la réunion de deux parties non vides Σ₁ et Σ₂ telles que aucun point de Σ₁ n'est entre deux points de Σ₂, et vice-versa alors, il existe un point O appartenant à ]AB[ tel que pour tous points M₁ et M₂ de ]AB[ autres que O, on a M₁*O*M₂ si et seulement si M₁ appartient à Σ₁ et M₂ appartient à Σ₂.

Propriété Dkd1 (Dkp_segment,O1,O2,O3,PO7,PO8): L’axiome de Dedekind implique que : Σ₁⋂Σ₂ ⊂{O}.

Démonstration de Ddk1 :
D'après l'axiome Dkp_segment :
O∈]AB[ donc A*O*B
Supposons que M∈Σ₁⋂Σ₂ avec M ≠ O.
M∈Σ₁⋂Σ₂=]AB[ donc A*M*B
D’après l’axiome O3, on a : M*A*O ou A*M*O ou A*O*M
1^er cas : si M*A*O
M*A*O et A*O*B donc d’après la propriété PO8, on a : M*A*B.
Ce qui est impossible d’après l’axiome O3, car A*M*B.
2^ième Cas : si A*M*O
D’après l’axiome O2, il existe un point M’ tel que O*M’*B.
A*O*B et A*M*O donc d’après la propriété PO7, on a : M*O*B.
O*M’*B et M*O*B donc d’après l’axiome O1, on a : B*M’*O et B*O*M.
B*M’*O et B*O*M donc d’après la propriété PO7, on a : M’*O*M.
M’*O*M donc d’après l’axiome O1, on a : M*O*M’.
M∈Σ₁⋂Σ₂ donc M∈Σ₁
M*O*M’ et M∈Σ₁ donc M’∈Σ₂
M∈Σ₁⋂Σ₂ donc M∈Σ₂
M*O*M’ et M∈Σ₂ donc M’∈Σ₁
O∈]AB[ , et ]AB[ = Σ₁⋃Σ₂ donc O∈Σ₁ et/ou O∈Σ₂.
Si O∈Σ₁, alors M*O*M’, M∈Σ₂, O∈Σ₁ et M’∈Σ₂.
Si O∈Σ₂, alors M*O*M’, M∈Σ₁, O∈Σ₂ et M’∈Σ₁.
Ce qui est impossible car d'après l'axiome Dkp_segment : aucun point de Σ₁ n'est entre deux points de Σ₂, et vice-versa.
3^ième cas : si A*O*M
A*O*M et A*O*B donc d’après la propriété PO7, on a : O*M*B.
O*M*B donc d’après l’axiome O1, on a : B*M*O.
Ceci revient à faire le 2^ième cas.
Donc c’est impossible.
CQFD

Propriété Dkd2 (Dkp_segment,O1,O2,O3,PO7,PO8): Dans l’axiome de Dedekind, le point O est unique.

Démonstration de Ddk2 :
Supposons qu’il existe deux points O₁ et O₂ candidats pour être le point O tel que défini par l’axiome Dkp_segment.
O₁∈]AB[ donc A*O₁*B
O₂∈]AB[ donc A*O₂*B
Donc d’après l’axiome O3, on : A*O₁*O₂ ou O₁*A*O₂ ou O₁*O₂*A.
1^er CAS : si O₁*A*O₂
O₁*A*O₂ et A* O₂*B, donc d’après la propriété PO7, on a : O₁*A*B.
Donc A*O₁*B et O₁*A*B, ce qui est impossible d’après l’axiome O3.
2^ième CAS : si A*O₁*O₂
(le cas O₁*O₂*A est le même cas, car on peut inverser les notations de O₁ et O₂)
D’après l’axiome O2, appliqué à la droite (AB) et aux points A et O₁ :
Il existe un point E te que A*E*O₁.
D’après l’axiome O2, appliqué à la droite (AB) et aux points O₁ et O₂ :
Il existe un point F te que O₁*F*O₂.
D’après l’axiome O2, appliqué à la droite (AB) et aux points O₂ et B :
Il existe un point G te que O₂*G*B.
A*E*O₁ et A*O₁*O₂ donc d’après la propriété PO7, on a : E*O₁*O₂.
E*O ₁*O₂ et O₁*F*O₂ donc d’après l’axiome O1, on a : O₂* O₁*E et O₂*F*O_1.
O₂*O₁*E et O₂*F*O₁ donc d’après la propriété PO7, on a : F*O₁*E.
F*O₁*E donc d’après l’axiome O1, on a : E*O₁*F.(*)
O₂*G*B et A*O₂*B et donc d’après l’axiome O1 , on a : B*G*O₂ et B*O₂*A.
B*G*O₂ et B*O₂*A donc d’après la propriété PO7, on a : G*O₂*A.
G*O₂*A donc d’après l’axiome O1 , on a : A*O₂*G.
A* O₁* O₂ et A*O₂*G et donc d’après la propriété PO7, on a : O ₁* O ₂*G.
O₁*F*O₂ et O₁*O₂*G donc d’après la propriété PO7, on a : F*O₂*G.(**)
Si, par exemple, on a : E∈Σ₁, donc d’après (*), on a : F∈Σ₂.
F∈Σ₂ donc d’après (**), on a : G∈Σ₁
O₁*F*O₂ et E*O₁*O₂ donc d’après l’axiome O1, on a : O₂*F*O₁ et O₂*O₁*E.
O₂*F*O₁ et O₂*O₁*E donc d’après la propriété PO7, on a : O₂*F*E.
O₂*F*E donc d’après l’axiome O1, on a : E*F*O₂.
E*F*O₂ et F*O₂*G donc d’après la propriété PO8, on a : E*F*G.
Ce qui est impossible car aucun point de Σ₁ n'est entre deux points de Σ₂, et vice-versa.
Donc nous avons bien l’unicité du point O dans l’axiome Dkp_segment.
CQFD

Propriété Dkd3 : Axiome de Dedekind sur la droite
Si l’ensemble des points d’une droite (d) soit la réunion Σ₁ et Σ₂ de deux parties non vides et telles que aucun point de Σ₁ ne soit entre deux points de Σ₂ et vice-versa, alors il existe un point O de (d) tel que pour tous points M₁ et M₂ de (d) autre que O, on ait M₁*O*M₂ si et seulement si M₁∈Σ₁ et M₂∈Σ₂.

Démonstration de Ddk3 :

Soient M₁∈Σ₁ et M₂∈Σ₂

Axiome de Dedekind :
Si l’ensemble des points d’une droite (d) soit la réunion Σ₁ et Σ₂ de deux parties non vides et telles que aucun point de Σ₁ ne soit entre deux points de Σ₂ et vice-versa, alors il existe un point O de (d) tel que pour tous points M₁ et M₂ de (d) autre que O, on ait M₁*O*M₂ si et seulement si M₁∈Σ₁ et M₂∈Σ₂.

Propriété : Dans l’axiome de Dedekind, le point O est unique.

Démonstration :
Supposons qu’il existe deux points O₁ et O₂ qui sont tous les deux des candidats pour être le point O tel que défini par l’axiome de Dedekind.
D’après l’axiome O2, il existe un point A, B, C de (d) tels que A*O₁*O₂, O₁*B*O₂ et O₁*O₂*C.

Sans perte de généralité, on peut prendre l’hypothèse que par exemple : A∈Σ₂

A*O₁*O₂, O₁*B*O₂
Donc d’après l’axiome O1, on a : O₂*O₁*A, O₂*B*O₁
Donc O₂*B*O₁ et O₂*O₁*A
Donc d’après la propriété PO7, on a : B*O₁*A
Donc d’après l’axiome O1, on a : A*O₁*B
A∈Σ_2, A*O₁*B donc B∈Σ₁

O₁*B*O₂, O₁*O₂*C
Donc d’après la propriété PO8, on a : B*O₂*C
B∈Σ₁, B*O₂*C donc C∈Σ₂

A*O₁*B, O₁*B*O₂ donc d’après la propriété PO7, on a : A*B*O₂
A*B*O₂, B*O₂*C donc d’après la propriété PO7, on a : A*B*C

Donc A∈Σ₂, B∈Σ_1, C∈Σ₂ et A*B*C, ce qui contradictoire avec aucun point de Σ₁ ne soit entre deux points de Σ₂.
Donc nous avons bien l’unicité du point O dans l’axiome de Dedekind. CQFD

Propriété (C1,C2,C3,O3,PO3,PO5,PO7, Dedekind,PC1): Postulat d'Archimède
Si A≠B, E∈[AB), alors il existe un point C∈[AB) et un entier n tel que : n [AB] ≅ [AC] et E∈[AC].

Démonstration du Postulat d'Archimède :

Si E∈[AB], alors n=1 et C=B. C’est démontré !
Donc nous pouvons considérer que E∉[AB].

Posons A₀ = A et A₁ = B.
E∉[A₀A₁] car nous considérons que E∉[AB].

Puis construisons, la suite de points (A_n) suivante :
Pour tout entier n≥2, on a : A_n+1 est tel que A₀*A_n*A_n+1 et [A₀A₁] ≅ [A_nA_n+1].
D’après l’axiome C1 et par récurrence, nous avons l’unicité et l’existence de cette suite de points.

Supposons que pour tout entier n≥2, E ∉ [A₀A_n].
Posons Σ₁={ M∈(A₀A₁) \ ∃n∈IN^* M∈[A₀A_n] }⋃[A₁A₀) et Σ₂=(A₀A₁) \ Σ₁

Montrons que Σ₁ et Σ₂ vérifient l’hypothèse de l’axiome de Dedeking.

E∉[AB]= [A₀A₁], et aussi pour tout entier n≥2, E ∉ [A₀A_n].
donc E∉{ M∈(A₀A₁) \ ∃n∈IN^* M∈[A₀A_n] }

D’après l’axiome O3, entre les cas E*A₀*A₁, A₀*E*A₁, A₀*A₁*E un seul est possible.
E∉[A₀A₁] donc on ne peut avoir A₀*E*A_1,
et E∈[AB)=[A₀A₁) donc A₀*A₁*E
donc on ne peut avoir E*A₀*A₁
donc E ∉[A₁A₀)
donc E∉Σ₁

E∈[AB)=[A₀A₁) donc E∈(A₀A₁)
E∉Σ₁
donc E∈Σ₂
donc Σ₂ est une partie non vide.

A₀∈Σ₁
donc Σ₁ est une partie non vide aussi.

Et par construction, on a : Σ₁⋂Σ₂= ∅.

Montrons que aucun point de Σ₁ n’est entre deux points de Σ_2.
Supposons qu’il existe Y₁*X*Y₂ tels que : Y₁∈Σ₂, X∈Σ₁ et Y₂∈Σ₂

Y₁∈Σ₂
Σ₂=(A₀A₁) \ Σ₁
Σ₁={ M∈(A₀A₁) \ ∃n∈IN^* M∈[A₀A_n] }⋃[A₁A₀)
donc Y₁∉ [A₁A₀)
donc d’après l’axiome O3, on a : A₀*A₁*Y₁

Y₂∈Σ₂
Σ₂=(A₀A₁) \ Σ₁
Σ₁={ M∈(A₀A₁) \ ∃n∈IN^* M∈[A₀A_n] }⋃[A₁A₀)
donc Y₂∉ [A₁A₀)
donc d’après l’axiome O3, on a : A₀*A₁*Y₂

Donc si (d) est une droite passant par A₁ et différente de (A₀A₁), alors d’après PO3 :
Y₁ appartient au demi-plan (P_Y1,d) et A₀ à l’autre (P’_A0,d)

A₀*A₁*Y₂ donc Y₂∈(A₀A₁) et Y₂∉[A₁A₀) donc d’après PO5, on a : Y₂ ∈ (P_Y1,d).

A₀,Y₁ et Y₂ appartiennent à la même droite et sont distincts car Y₁*X*Y₂ et Y₁,Y₂∉ [A₁A₀)
donc d’après l’axiome O3, on a : A₁*Y₁*Y₂ ou Y₁*A₁*Y₂ ou Y₁*Y₂*A₁ un seul cas est possible.

Y₁*A₁*Y₂ est impossible car Y₁ et Y₂ sont dans le même demi-plan (P_Y1,d).
Donc Y₂∈]A₁Y1)⊂ (P_Y1,d)
Donc [Y₁Y₂] ⊂ (P_Y1,d) et A₁*Y₁*Y₂ ou Y₁*Y₂*A₁
Donc [Y₁Y₂] ⊂ (P_Y1,d) et A₁*Y₁*Y₂ ou A₁*Y₂*Y₁

Y₁*X*Y₂ donc X∈[Y₁Y₂] ⊂ (P_Y1,d)
Et donc X∉[A₁A₀)

Mais X∈Σ₁ donc il existe un entier n≥1 tel que X∈[A₀A_n]

Si A₁*Y₁*Y₂, comme Y₁*X*Y₂, alors d’après PO7, on aurait : A₁*Y₁*X.
donc Y₁ ∈[A₁A_n] ⊂ Σ₁ Ce qui est impossible
Si A₁*Y₂*Y₁, comme Y₂*X*Y₁, alors d’après PO7, on aurait : A₁*Y₂*X.
donc Y₂∈[A₁A_n] ⊂ Σ₁ Ce qui est impossible

Donc aucun point de Σ₁ ne soit entre deux points de Σ_2.

Montrons que aucun point de Σ₂ n’est entre deux points de Σ_1.
Supposons qu’il existe X₁*Y*X₂ tels que : X₁∈Σ₁, Y∈Σ₂ et X₂∈Σ₁

Y∈Σ₂
Σ₂=(A₀A₁) \ Σ₁
Σ₁={M∈(A₀A₁) \ ∃n∈IN^* M∈[A₀A_n] }⋃[A₁A₀)
Donc Y∉ [A₁A₀)
Donc d’après l’axiome O3, on a : A₀*A₁*Y

X₁*Y*X₂ donc Y∈[X₁X₂]
Si X₁∈[A₁A₀) et X₂∈[A₁A₀), alors Y∈[X₁X₂] ⊂[A₁A₀). Ce qui est impossible car Y∉[A₁A₀)

Donc X₁∉[A₁A₀) ou X₂∉[A₁A₀)
Donc choisissons X₁∉[A₁A₀), le même raisonnement peut être fait pour X₂∉[A₁A₀).
D’après l’axiome O3, on a : A₀*X₁*Y ou X₁*A₀*Y ou A₀*Y₂*X₁ un seul cas est possible

1^er cas : Si A₀*Y₂*X₁ :
Comme X₁∈Σ₁, il existe un entier n≥1 tel que X₁∈[A₀A_n].
Y₂∈[A₀X₁] ⊂ [A₀A_n] ⊂ Σ₁ Ce qui est impossible

2^ième cas : Si X₁*A₀*Y :
D’après PO7, comme X₁*A₀*Y et X₁*Y*X₂, on a : A₀*Y*X₂
On sait que A₀*A₁*Y
Si X₂∈[A₁A₀)\[A₁A₀], alors X₂*A₀*A₁
Donc A₀*A₁*Y et X₂*A₀*A1, on aurait d’après PO7 : X₂*A₀*Y.
Ce qui est impossible d’après l’axiome O3.
Donc X₂∈[A₀A₁)
Donc comme X₂∈Σ₁, il existe un entier n≥1 tel que X₂∈[A₀A_n].
Et A₀*Y*X₂ donc Y ∈[A₀X₂] ⊂ [A₀A_n] ⊂ Σ₁ Ce qui est impossible

3^ième cas : si A₀*X₁*Y
D’après PO8, comme A₀*X₁*Y et X₁*Y*X₂, on a : A₀*Y*X₂
On sait que A₀*A₁*Y
Si X₂∈[A₁A₀)\[A₁A₀], alors X₂*A₀*A₁
Donc A₀*A₁*Y et X₂*A₀*A1, on aurait d’après PO7 : X₂*A₀*Y.
Ce qui est impossible d’après l’axiome O3.
Donc X₂∈[A₀A₁)
Donc comme X₂∈Σ₁, il existe un entier n≥1 tel que X₂∈[A₀A_n].
Et A₀*Y*X₂ donc Y ∈[A₀X₂] ⊂ [A₀A_n] ⊂ Σ₁ Ce qui est impossible
Donc aucun point de Σ₂ n’est entre deux points de Σ₁.

Donc nous pouvons appliquer l’axiome de Dedekind : (A₀A₁) est donc la réunion Σ₁ et Σ₂ de deux parties non vides et telles que aucun point de Σ₁ ne soit entre deux points de Σ₂ et vice-versa, donc il existe un point F de (A₀A₁) tel que pour tous points M₁ et M₂ de (A₀A₁) autre que F, on ait M₁*F*M₂ si et seulement si M₁∈Σ₁ et M₂∈Σ₂.

Montrons que F ∈[A₀E[.

Soit E’ un point de (A₀A₁) tel que A₀*E’*E et [E’E] ≅ [A₀A₁].
E∉[A₀A₁] et E∈[A₀A₁) donc A₀*A₁*E
Donc d’après PC1, il existe E’ un point de (A₀E) tel que A₀*E’*E et [E’E] ≅ [A₀A₁].

Supposons que E’∈Σ₁
Alors il existerait un entier n tel que E’∈[A₀A_n]
Et donc [A₀E’]<[A₀A_n]
Donc il existe H tel que A₀*H*A_n et [HA_n] ≅ [A₀E’]
[E’E] ≅ [A₀A₁] ≅ [A_nA_n+1]

Donc [HA_n] ≅ [A₀E’] et [A_nA_n+1] ≅ [E’E]
A₀*H*A_n et A₀*A_n*A_n+1 donc d’après PO7, on a : H*A_n*A_n+1
Et on a aussi A₀*E’*E.
Donc d’après l’axiome C3, on a : [HA_n+1] ≅ [A₀E]

A₀*H*A_n et A₀*A_n*A_n+1 donc d’après PO7, on a : A₀*H*A_n+1
Donc [HA_n+1]<[A₀A_n+1]

Donc d’après l’axiome C2, on a : [A₀E]< [A₀A_n+1]
Donc E∈Σ₁ Ce qui est contraire à l’hypothèse.
Donc E’∉Σ₁
Donc E’∈Σ₂

Prenons maintenant un point E’’ tel que A₀*E*E’’
Supposons que E’’∈Σ₁
A₀∈Σ₁, E∈Σ_2, E’’∈Σ₁ Impossible car aucun point de Σ₂ n’est entre deux points de Σ₁.
Donc E’’∈Σ₂
Et donc F n’est pas après E
Et en particulier :
A₀*E’*E et A₀*E*E’’ donc d’après PO7, on a : E’*E*E’’
Donc E ≠ F car si E = F, alors E’*E*E’’ => E’ et E’’ sont dans Σ₁ et Σ₂

Prenons enfin un point E’’’ tel que E’’’*A₀*E
Supposons que E’’’∈Σ₂
E’’’∈Σ_2, A₀∈Σ₁, E∈Σ₂ Impossible car aucun point de Σ₁ n’est entre deux points de Σ₂.
Donc E’’’∈Σ₁
Donc F n’est pas avant A₀

Donc F ∈[A₀E[.

Pour finir remplaçons, E par F est recommençons tout ce raisonnement :
Par application de Dedekind nous trouvons un F’ tel que :
Pour Σ₁’={ M∈(A₀A₁) \ ∃n∈IN^* M∈[A₀A_n] }⋃[A₁A₀) et Σ₂’=(A₀A₁) \ Σ₁’, F’∈[A₀F[et pour tous points M₁ et M₂ de (A₀A₁) autre que F’, on ait M₁*F*M₂ si et seulement si M₁∈Σ₁’ et M₂∈Σ₂’

F’∈[A₀F[
Donc A₀*F’*F et A₀*F*E, donc d’après PO7, on a : F’*F*E
Mais E∈Σ₂, donc F’∈Σ₁
F’ n’est pas avant A₀
Donc il existe un entier n≥1 tel que F’∈[A₀A_n]. Ce qui est impossible.

Le fait qu'un cercle et un segment de droite AB soient sécants signifie qu'il existe au moins un point qui appartient à la fois au cercle et au segment de droite. Dans cette démonstration, nous allons montrer qu'un tel point existe en utilisant l'axiome de Dedekind.
Premièrement, nous définissons ce qu'est un cercle. En géométrie euclidienne, un cercle est défini comme l'ensemble des points qui sont à une distance fixe (le rayon) d'un certain point (le centre). Nous allons utiliser cette définition pour notre démonstration.
Puis, nous avons les conditions suivantes :
Soit un cercle de centre O et de rayon R.
Soit un segment de droite AB avec le point A à l'intérieur du cercle et le point B à l'extérieur du cercle.
Nous allons prouver qu'il existe un point M sur le segment AB qui se trouve aussi sur le cercle.
La démonstration procède comme suit :
Considérez les points sur le segment AB comme étant divisés en deux ensembles, Σ1 et Σ2, selon qu'ils sont à l'intérieur ou à l'extérieur du cercle. Autrement dit, un point M sur AB appartient à Σ1 si la distance de M à O est inférieure ou égale à R (c'est-à-dire si M est à l'intérieur du cercle ou sur le cercle), et à Σ2 si la distance de M à O est supérieure à R (c'est-à-dire si M est à l'extérieur du cercle).
Il est clair que A appartient à Σ1 et B appartient à Σ2, donc Σ1 et Σ2 sont tous deux non vides.
De plus, aucun point de Σ1 n'est entre deux points de Σ2, et vice versa. En effet, si M1 et M2 sont deux points de Σ1, alors la distance entre O et tout point entre M1 et M2 ne peut pas être supérieure à R, donc aucun point de Σ2 ne peut être entre M1 et M2. De même, si N1 et N2 sont deux points de Σ2, alors la distance entre O et tout point entre N1 et N2 doit être supérieure à R, donc aucun point de Σ1 ne peut être entre N1 et N2.
Par conséquent, les conditions de l'axiome de Dedekind sont remplies pour le segment AB, Σ1 et Σ2. Par cet axiome, il existe donc un point unique O' sur le segment AB tel que pour tout point M sur AB autre que O', M est dans Σ1 si et seulement si A*O'M, et M est dans Σ2 si et seulement si MO'*B.
Ce point O' doit être à la frontière entre Σ1 et Σ2, donc la distance entre O et O' est exactement R, ce qui signifie que O' est sur le cercle. De plus, comme O' est sur AB, le cercle et le segment AB sont donc sécants au point O'.Haut du formulaire
Bas du formulaire

Liaisons

Graph

William BOURGES © 2023