L'icosaèdre régulier est un solide convexe à 20 faces.
Les faces sont des triangles équilatéraux.
L'icosaèdre comporte 12 sommets et 30 arêtes.
L'icosaèdre régulier est l'un des 5 solides de Platon (polyèdres réguliers convexes : tétraèdre, cube, octaèdre, dodécaèdre pentagonal et icosaèdre).
Dans le repère orthonormé utilisé ici les coordonnées des 12 sommets sont :
(± φ, ± 1, 0); (0, ± φ, ± 1); (± 1, 0, ± φ);
avec : φ = ½(1 +√5) ≈ 1,6180 (nombre d'or).
La symétrie de l'icosaèdre est celle du groupe Ih ( 5 3 m ).
Les éléments du groupe sont :
E, 12 C5, 12 C25, 20 C3, 15 C2, i,
12 S10,
12 S310, 20 S6 et 15 σ.
Plus simplement les éléments de symétrie de l'icosaèdre sont : 6 A5, 10 A3, 15 A2, 15 M et C.
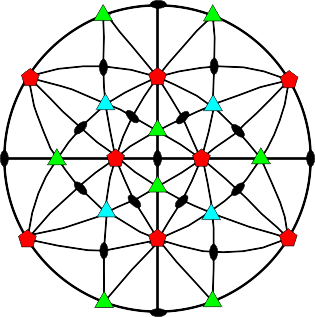 |
La figure ci-contre est la projection stéréographique des éléments de symétrie du groupe Ih. (
6 A5, 10 A3, 15 A2, 15 M et C) Attention |
Utilisation
Glisser la souris dans le cadre pour
modifier l'orientation des objets.
Les faces situées en arrière du plan de projection sont tracées en gris en mode transparent.
