Un dioptre est la séparation entre deux milieux transparents homogènes d'indices N1 et N2. On examine le dioptre sphérique dans l'approximation des petits angles d'incidence.

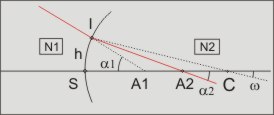Le rayon du dioptre est R = SC On assimile l'arc SI à la droite SI et on pose h = SI. Un rayon incident frappe le dioptre avec l'incidence i = α1 − ω i = − h / SA1 + h / SC L'angle de réfraction est r = ω − α2= h / SC − h / SA2 La relation de Descartes conduit à : N1 ( 1 / SC − 1 / SA1) = N2 ( 1 / SC − 1 / SA2) (a)

Quand le point objet est à l'infini, on dit que le point image est le foyer image Fi. Il est tel que SFi = fi = SC.N2 / (N2 − N1).
De même si le point image est à l'infini, le point objet est situé au foyer objet Fo tel que SFo = fo = SC.N1 / (N1 − N2).
Noter que si SA1 = SC alors SA2 = SC. On vérifie qu'un rayon passant par le centre du dioptre n'est pas dévié.
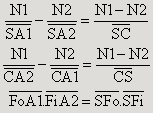
La relation de conjugaison (a) utilise le sommet du dioptre comme origine.
En déduire les relations de conjugaison qui utilisent le centre ou les foyers comme origines.

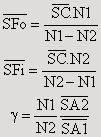Remarques :
En faisant R = ∞ on retrouve les formules du dioptre plan.
En faisant N2 = − N1, on retrouve les formules des miroirs sphériques.

Construction des images.
Un objet A1B1 donne une image A2B2. Si A1 est sur l'axe optique A2 est également sur cet axe. Pour construire B2, On utilise des rayons particuliers.
* Tous les rayons passant par le centre du dioptre ne sont pas déviés.
* Tous les rayons parallèles à l'axe optique (qui correspondent à un objet à l'infini) passent par le foyer image.
* Tous les rayons issus du foyer objet émergent parallèlement à l'axe optique.
Pour les constructions, on utilise les deux premiers rayons.

Cas des objets à l'infini.
Si le plan objet est à l'infini, le plan image est dans le plan focal image. Pour un faisceau faisant l'angle θ avec l'axe optique, le point de convergence est situé à l'intersection du plan focal image avec le rayon passant par O, incliné de θ sur l'axe optique.

Le dioptre est dit convergent si un faisceau parallèle avant le dioptre converge à la sortie. Dans le cas contraire, il est divergent.
On peut noter que pour un dioptre convergent, le centre de courbure est situé dans le milieu d'indice le plus grand .

Utilisation
Le programme permet de choisir R positif ou négatif et N1 > N2 ou N1 < N2.
Vérifier que les 4 cas possibles correspondent en fait à un dioptre divergent et à un dioptre convergent (principe du retour inverse de la lumière).
Le programme permet d'étudier aussi le cas N2 = − N1 qui correspond au miroir mais dans ce cas, l'échelle utilisée n'est pas optimale.
Pour vérifier les formules de conjugaison, le curseur cyan permet de repérer les différentes positions.