Sommaire : Premiere_ipynb
1.2 - Binaire d'un entier relatif ✔
1.3 - Nombres réels ✔
1.4 - Expressions booléennes ✔
1.5 - ASCII, ISO, Unicode ✔
2.1 - p-uplets ✔
2.2 - Tableau ✔
2.3 - Dictionnaire ✔
3.1 - CSV Indexation ✔
3.2 - CSV Recherche ✔
3.3 - CSV Tri ✔
3.4 - CSV Fusion ✔
4.1 - IHM ✔
4.2 - Requêtes HTTP ✔
4.3 - GET POST ✔
5.1 - Von Neumann ✔
5.2 - Réseau 1 ✔
5.3 - Réseau 2 ✔
5.4 - OS ✔
5.5 - Périphériques ✔
6.0 - Elémentaires ✔
6.1 - Elémentaires (Correction) ✔
6.2 - Langages ✔
6.3 - Spécification
6.4 - Mise au point de programmes ✔
6.5 - Bibliothèques ✔
7.1 - Parcours séquentiel ✔
7.2 - Tri par insertion, par sélection ✔
7.3 - k plus proches voisins ✔
7.4 - Dichotomique tableau trié ✔
7.5 - Algorithmes gloutons ✔
1.1 - Entier dans une base b ✔
Première NSI
Représentation des données: types et valeurs de base
Écriture d’un entier positif dans une base b ≥ 2.
Capacités attendues :
Passer de la représentation d’une base dans une autre;
-Évaluer le nombre de bits nécessaires à l’écriture en base 2 d’un entier, de la somme ou du produit de deux nombres entiers
Commentaires :
Les bases 2, 10 et 16 sont privilégiées.
Il s’agit de décrire les tailles courantes des entiers (8, 16, 32 ou 64 bits).
Il est possible d’évoquer la représentation des entiers de taille abitraire de Python.
1) Les bases
C’est l’usage d’une base qui permettra de répondre au mieux aux contraintes posées.
Au lieu de compter uniquement par unités, on compte "par paquets". La plus fréquente est la base décimale (10), mais on trouve également :
— la base sexagésimale (60), utilisée par les Sumériens et parfois au moyen âge en France,
— la base vicésimale (20), utilisée par les Mayas ou duodécimale (12),
— la quinaire (5), utilisée aussi par les Mayas,
— et la binaire (2) utilisé en électronique numérique et informatique,
— la base 16 (système hexadécimal), en informatique, facilitant les conversions en base 2 en regroupant des chiffres binaires...
2) La notion de base
Une base de numération désigne la valeur dont les puissances successives interviennent dans l’écriture des nombres dans la numération positionnelle.
En base n , on a donc besoin de n chiffres (digits), de 0 à n − 1.
Par exemple :
-
en base 10, on a besoin de 10 chiffres, de 0 à 9,
-
en base 2, on a besoin de 2 chiffres de 0
-
Pour les bases supérieures à 10, il faut d’autres chiffres. On aurait pu inventer des symboles nouveaux. On convient plutôt d’utiliser les premières lettres de l’alphabet. Pour la base 16, on utilise les chiffres de 0 à 9 puis A (pour 10), B (pour 11), C (pour 12) ... , F (pour 15)
def generate_table(n):
print(" Décimal | Binaire | Hexadécimal")
for i in range(n):
decimal_format = i
binary_format = bin(i).replace("0b", "")
hexadecimal_format = hex(i).replace("0x", "").upper()
print(f" {decimal_format:>7} | {binary_format:>9} | {hexadecimal_format:>11}")
generate_table(16) Décimal | Binaire | Hexadécimal
0 | 0 | 0
1 | 1 | 1
2 | 10 | 2
3 | 11 | 3
4 | 100 | 4
5 | 101 | 5
6 | 110 | 6
7 | 111 | 7
8 | 1000 | 8
9 | 1001 | 9
10 | 1010 | A
11 | 1011 | B
12 | 1100 | C
13 | 1101 | D
14 | 1110 | E
15 | 1111 | F
def display_formats(decimal_number):
print("Décimal | Binaire | Hexadécimal")
binary_format = bin(decimal_number).replace("0b", "")
hexadecimal_format = hex(decimal_number).replace("0x", "").upper()
print(f"{decimal_number:7} | {binary_format:9} | {hexadecimal_format:11}")
display_formats(456)Décimal | Binaire | Hexadécimal
456 | 111001000 | 1C8
Exemples :
-
décomposition de 456 en base 10 :
$456_{10} = 4 \times 10^2 + 5 \times 10^1 + 6 \times 10^0$ -
décomposition de 100110011000 en base 2: $111001000_2\ = 1 \times 2^8 + 1 \times 2^7 + 1 \times 2^6 + 0 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 \ = 2^8 + 2^7 + 2^6 + 2^3 \ = 256 + 128 + 64 + 8 \ = 456_{10} $
-
décomposition de 1C8 en base Hexadécimale : $1C8_{16}\ = 1 \times 16^2 + C \times 16^1 + 8 \times 16^0 \ = 1 \times 16^2 + 12 \times 16^1 + 8 \times 16^0 \ = 256 + 192 + 8\ = 456_{10}$
Remarque :
Grâce à ces exemples, nous savons déjà passer de la base 2 ou 16 à la base 10.
Méthode pour décomposer un nombre en base 10 en la base 2
On procède par divisions successives par 2 des quotients, et on récupère les restes :
- On le divise par 2 et on note le reste de la division (c’est soit un 1 soit un 0).
- On refait la même chose avec le quotient précédent, et on met de nouveau le reste de coté.
- On réitère la division, et ce jusqu’à ce que le quotient est 0.
- Le nombre en binaire apparaît : le premier à placer est le dernier reste non nul.
- Ensuite, on remonte en plaçant les restes que l’on avait, en les plaçant à droite du reste précédent.
Exemple :
Conversion du nombre 456 en binaire : $$ 456 = 2 _ 228 + 0\ 228 = 2 _ 114 + 0\ 114 = 2 _ 57 + 0\ 57 = 2 _ 28 + 1\ 28 = 2 _ 14 + 0\ 14 = 2 _ 7 + 0\ 7 = 2 _ 3 + 1\ 3 = 2 _ 1 + 1\ 1 = 2 * 0 + 1\ $$ Le nombre 456 en binaire est : 111001000
donc $$456_{10} = 111001000_2$$
def afficher_division(n, diviseur):
quotient = n // diviseur
reste = n % diviseur
print(f"{n} = {diviseur} x {quotient} + {reste}")
return quotient, reste
n = 456
print(f"Conversion du nombre {n} en binaire :\n")
temp = n
binary_representation = []
while temp > 0:
temp, remainder = afficher_division(temp, 2)
binary_representation.append(remainder)
binary_number = "".join(map(str, binary_representation[::-1]))
print(f"Le nombre {n} en binaire est : {binary_number}")Conversion du nombre 456 en binaire : 456 = 2 x 228 + 0 228 = 2 x 114 + 0 114 = 2 x 57 + 0 57 = 2 x 28 + 1 28 = 2 x 14 + 0 14 = 2 x 7 + 0 7 = 2 x 3 + 1 3 = 2 x 1 + 1 1 = 2 x 0 + 1 Le nombre 456 en binaire est : 111001000
Méthode pour décomposer un nombre en base 10 en la base 16
On procède par divisions successives par 16 des quotients, et on récupère les restes :
- On le divise par 16 et on note le reste de la division (c’est un nombre de 0 soit un 15).
- On refait la même chose avec le quotient précédent, et on met de nouveau le reste de coté.
- On réitère la division, et ce jusqu’à ce que le quotient est 0.
- Le nombre en hexadécimal apparaît : le premier à placer est le dernier reste non nul.
- Ensuite, on remonte en plaçant les restes que l’on avait, en les plaçant à droite du reste précédent.
Exemple :
Conversion du nombre 456 en hexadécimal :
$456 = 16 _ 28 + 8$ et $8_{10} = 8_h$
$28 = 16 _ 1 + 12$ et $12_{10} = C_h$
$1 = 16 * 0 + 1$ et $1_{10} = 1_h$
Le nombre 456 en hexadécimal est : 1C8
donc $456_{10} = 1C8_h$
autre méthode (à réfléchir!):
$456_{10}$
$= 111001000_2$
$= 0001 \ 1100 \ 1000_2$
$= 1C8_h$
ou encore :
$456_{10}\
= 111001000_2\
= 1 \times 2^8 + 1 \times 2^7 + 1 \times 2^6 + 0 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 \
= (1 \times 2^0)2^8 + (1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0) 2^4 + 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 \
= (1 \times 2^0) (2^4)^2 + (1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0) 2^4 + 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 \
= (1 \times 2^0) 16^2 + (1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0) 16^1 + 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 \
= 1 \times 16^2 + 12 \times 16^1 + 8 \times 16^0\
= 1C8_h
$
def afficher_division(n, diviseur):
quotient = n // diviseur
reste = n % diviseur
print(f"{n} = {diviseur} x {quotient} + {reste}")
return quotient, reste
def convert_to_hexadecimal(n):
hex_values = '0123456789ABCDEF'
hex_representation = []
while n > 0:
n, remainder = afficher_division(n, 16)
hex_representation.append(hex_values[remainder])
return "".join(hex_representation[::-1])
n = 456
print(f"Conversion du nombre {n} en hexadécimal :\n")
hex_number = convert_to_hexadecimal(n)
print(f"Le nombre {n} en hexadécimal est : {hex_number}")Conversion du nombre 456 en hexadécimal : 456 = 16 x 28 + 8 28 = 16 x 1 + 12 1 = 16 x 0 + 1 Le nombre 456 en hexadécimal est : 1C8
Remarque
Pour convertir un nombre de la base 10 à la base 2 avec Python, il y a la commande bin().
Pour convertir un nombre de la base 10 à la base 16 avec Python, il y a la commandehex().
Pour convertir un nombre de la base 2 ou 16 à la base 10 avec Python, il y a la commande int( ,2) ou int( ,16).
n = 456
binary_representation = bin(n)
print(f"Le nombre {n} en binaire est : {binary_representation}")
n = 456
hex_representation = hex(n)
print(f"Le nombre {n} en hexadécimal est : {hex_representation}")
binary_str = "111001000" # Exemple d'une chaîne binaire pour 456 en décimal
decimal_number = int(binary_str, 2)
print(f"Le nombre {binary_str} en binaire est égal à {decimal_number} en décimal.")
hex_str = "1C8" # Exemple d'une chaîne hexadécimale pour 456 en décimal
decimal_number = int(hex_str, 16)
print(f"Le nombre {hex_str} en hexadécimal est égal à {decimal_number} en décimal.")
Le nombre 456 en binaire est : 0b111001000 Le nombre 456 en hexadécimal est : 0x1c8 Le nombre 111001000 en binaire est égal à 456 en décimal. Le nombre 1C8 en hexadécimal est égal à 456 en décimal.
Exercices
EXERCICE 1
Ecrire les nombres binaires 1110, 10101, 1101 en base 10.
# Conversion en base 10
binary_numbers = ['1110', '10101', '1101']
decimal_representations = [int(b, 2) for b in binary_numbers]
list(zip(binary_numbers, decimal_representations))
EXERCICE 2
Ecrire les nombres décimaux suivant 124, 243, 10, 1058 en base 2, puis en base 16.
# Conversion en base 2 et 16
numbers = [124, 243, 10, 1058]
binary_representations = [bin(n).replace("0b", "") for n in numbers]
hex_representations = [hex(n).replace("0x", "").upper() for n in numbers]
list(zip(numbers, binary_representations, hex_representations))
EXERCICE 3
Faire les additions suivantes en base dix, puis en base 2 de 35 + 63 , 126 + 17 et enfin 2045 + 5307.
# Additions en base 10 et en base 2
pairs_to_add_ex3 = [(35, 63), (126, 17), (2045, 5307)]
decimal_sums_ex3 = [sum(pair) for pair in pairs_to_add_ex3]
binary_sums_ex3 = [bin(sum(pair)).replace("0b", "") for pair in pairs_to_add_ex3]
list(zip(pairs_to_add_ex3, decimal_sums_ex3, binary_sums_ex3))3) Nombre de bits nécessaires à l’écriture en base 2 d’un entier, de la somme ou du produit de deux nombres entiers
Nombre de bits nécessaire à l'écriture en binaire d'un entier naturel
Sur 8 bits le plus grand entier positif possible est 11111111 (soit 255) et le plus petit 00000000 (soit 0), on peut donc représenter $2^8$ entiers.
Sur n bits, il est possible de coder $2^n$ entiers.
Donc :
8 bits (1 octet), on peux coder $2^8 = 256$ entiers différents.
16 bits (2 octets), on peux coder $2^{16} = 65 535$ entiers différents.
32 bits (4 octets), on peux coder $2^{32} = 4 294 967 296$ entiers différents.
64 bits (8 octets), on peux coder $2^{64} =18 446 744 073 709 551 616$ entiers différents
Une question très fréquente est le nombre de bits nécessaire à l'écriture d'un entier.
Si k un entier naturel tel que $2^{n-1} ≤ k < 2^n$ et n est un entier, alors il faut au moins n bits pour écrire l'entier naturel k en binaire.
Preuve :
$k =a_{n-1} 2^{n-1} + ...+a_0 2^0$
$2^{n-2} + ...+2^0 = (2- 1)(2^{n-2} + ...+2^0) = (2^{n-1} + ...+2^1) - (2^{n-2} + ...+2^0) = 2^{n-1} - 1$
donc comme $2^{n-1} ≤ k$ alors $a_{n-1} = 1$ donc il faut au moins n bits.
Par exemple:
$2^4 ≤ 22 < 2^5$ donc il faut au moins 5 bits pour coder 22 en binaire.
Remarque :
$22_{10}=(10110)_2$
Nombre de bits nécessaire à l'écriture en binaire d'une somme de 2 entiers
Sur 4 bits le plus grand entier positif possible est 1111 (soit 15) et le plus petit 0 (soit 0).
Donc la plus grande somme possible est 30 soit en binaire $(11110)_2$ soit un bit de plus.
La somme de deux entiers naturels codés sur nn bits pourra être codée sur au plus n+1 bits.
Preuve :
$(2^n + ...+2^0)+(2^n + ...+2^0) = 2(2^n + ...+2^0) = 2^{n+1} + ...+2^1$
Nombre de bits nécessaire à l'écriture en binaire d'un produit de 2 entiers
Sur 4 bits le plus grand entier positif possible est 1111 (soit 15) et le plus petit 0 (soit 0).
Donc le plus grand produit possible est 15×15 = 225 soit en binaire $(11100001)_2$ donc sur 8 bits soit deux fois plus de bits.
Le produit de deux entiers naturels codés sur n bits avec n>1 pourra être codée au plus sur 2n bits.
Preuve :
$(2^n + ...+2^0)(2^n + ...+2^0) = ((2^n)^2 + ...+2^0) = 2^{2n} + ...+2^0$
Exercice 4 :
a) Si vous avez un entier codé sur 5 bits, combien d'entiers différents pouvez-vous coder avec ces 5 bits ?
b) Quel est le nombre minimum de bits nécessaires pour coder l'entier 40 en binaire ?
c) Si vous avez deux entiers, chacun codé sur 7 bits, quel est le nombre maximum de bits nécessaire pour coder leur somme ?
d )Si vous multipliez deux entiers, chacun codé sur 3 bits, quel est le nombre de bits du produit ?
1.2 - Binaire d'un entier relatif ✔
Représentation des données : types et valeurs de base
Représentation binaire d’un entier relatif.
Capacités attendues :
-Utiliser le complément à 2.
1 ) Une première représentation intuitive mais insatisfaisante : le binaire signé
Une idée simple pour représenter les entiers relatifs est d’utiliser le bit de poids fort (le plus à gauche) pour représenter le signe de l’entier : 0 pour un entier positif et 1 pour un entier négatif.et d’utiliser les autres bits pour représenter la valeur absolue de l’entier.
En procédant ainsi, si on code les entiers naturels sur 4 bits (pour simplifier), alors comme :$(010)_2=2$
- le binaire 0010 correspondant à l’entier 2 car le bit de poids fort est 0 donc il s’agit d’un entier positif;
- le binaire 1010 correspondant à l’entier (−2) car le bit de poids fort est 1 donc il s’agit d’un entier négatif.
donc on aurait : $(0010)_2 = 2_{10}$ et $(1010)_2 = -2_{10}$
\begin{array}{c c c c c} & & \color{red}1 & & \ & 0 & 0 & 1 & 0 \
- & 1 & 0 & 1 & 0 \ \hline & 1 & 1 & 1 & 0 \ \end{array}
mais $(0010)_2 + (1010)_2 = (1110)_2 = -6_{10}$ et $(0010)_2 + (1010)_2 = 2_{10} + -2_{10} = 0_{10}$
or $-6_{10}$ ≠ $0_{10}$
donc ce n’est donc pas une méthode satisfaisante car il faudrait alors redéfinir l’algorithme de l’addition.
La solution la plus commune pour contourner ces problèmes est d’utiliser l’encodage dit par complément à 2.
2) La représentation choisie : le complément à 2
Considérons que l’on code nos entiers sur n=4 bits (on peut généraliser tout ce qui sera vu). On ne s’intéresse ici qu’à la représentation des entiers négatifs.
Exemple : Représentation du nombre $(−5)_{10}$ par la méthode du complément à 2
Étape 1 : On passe d’abord en positif : $5_{10}$
Étape 2 : On représente 5 sur 4 bits : $0101_2$
Étape 3 : On inverse tous les bits (les 1 deviennent 0 et réciproquement) : $1010_2$
Étape 4 : On ajoute 1 au nombre obtenu (sans tenir compte de la retenue finale) : $1010_2 + 0001_2 = 1011_2$
\begin{array}{c c c c c} \color{red}1& \color{red}1 & \color{red}1 & \color{red}1 & \ & 0 & 1 & 0 & 1 \
- & 1 & 0 & 1 & 1 \ \hline \color{blue}1 & 0 & 0 & 0 & 0 \ \end{array}
et donc $0101_2 + 1011_2 = 0000_2$ sans tenir compte de la retenue finale car nous sommes sur 4 bits.
Et dans l'autre sens ?
Connaissant une représentation en complément à 2, il est bien sûr possible de déterminer de quel entier il s’agit.
Exemple : Quel entier est représenté par $1011_2$ en complément à 2 (sur 4 bits) ?
Étape 1 : On inverse tous les bits : $0100_2$
Étape 2 : On ajoute 1 au résultat : $0100_2 + 0001_2 = 0101_2$
Étape 3 : On décode l’entier positif obtenu : $0101_2 = 0×2^3 + 1×2^2 + 0×2^1 + 1×2^0 =5_{10}$
Étape 4 : On passe en négatif : $(−5)_{10}$
Conclusion : Donc $1011_2$ est la représentation en complément à 2 de l’entier $(−5)_{10}$ sur n=4 bits.
def int_from_signed_bin(binary_str):
"""Récupère un entier signé à partir d'une chaîne binaire."""
if binary_str[0] == "1": # Si le bit de signe est 1, le nombre est négatif
# Complément à deux pour obtenir la valeur absolue
n = -int(''.join('1' if b == '0' else '0' for b in binary_str), 2) - 1
else:
n = int(binary_str, 2)
return n
def display_signed_binaries(n):
"""Affiche toutes les représentations binaires sur n bits et leurs valeurs entières signées correspondantes."""
for i in range(2**n): # 2^n valeurs possibles pour n bits
binary_str = format(i, f'0{n}b') # Convertit en binaire avec zéro-padding
print(f"{binary_str} en binaire = {int_from_signed_bin(binary_str)} ")
# Test pour n=4
display_signed_binaries(4)
0000 en binaire = 0 0001 en binaire = 1 0010 en binaire = 2 0011 en binaire = 3 0100 en binaire = 4 0101 en binaire = 5 0110 en binaire = 6 0111 en binaire = 7 1000 en binaire = -8 1001 en binaire = -7 1010 en binaire = -6 1011 en binaire = -5 1100 en binaire = -4 1101 en binaire = -3 1110 en binaire = -2 1111 en binaire = -1
def int_to_twos_complement(val, n):
"""Convertit un entier relatif en complément à 2 de taille n."""
if val < 0:
val = (1 << n) + val
format_string = '{:0' + str(n) + 'b}'
return format_string.format(val)
def binary_addition(bin1, bin2, n):
"""Additionne deux nombres binaires de même longueur."""
bin1 = bin1.zfill(n)
bin2 = bin2.zfill(n)
carry = 0
result = ''
for i in range(n - 1, -1, -1):
bit_sum = carry + int(bin1[i]) + int(bin2[i])
result = str(bit_sum % 2) + result
carry = bit_sum // 2
# Ignore le dépassement hors de la plage de la taille n
return result[-n:]
def twos_complement_to_int(bin_str):
"""Convertit un binaire en complément à 2 en entier relatif."""
if bin_str[0] == '1':
return int(bin_str, 2) - (1 << len(bin_str))
else:
return int(bin_str, 2)
# Test
n = 8
val1 = 5
val2 = -3
bin1 = int_to_twos_complement(val1, n)
bin2 = int_to_twos_complement(val2, n)
sum_bin = binary_addition(bin1, bin2, n)
print(f"{val1} en binaire (complément à 2) = {bin1}")
print(f"{val2} en binaire (complément à 2) = {bin2}")
print(f"Somme des deux binaires = {sum_bin}")
print(f"{sum_bin} en entier relatif = {twos_complement_to_int(sum_bin)}")
5 en binaire (complément à 2) = 00000101 -3 en binaire (complément à 2) = 11111101 Somme des deux binaires = 00000010 00000010 en entier relatif = 2
3) Plage de valeurs possibles
Si on code sur 4 bits, il est possible de représenter $2^4$ entiers.
Dans la méthode du complément à 2 :
- la moitié sont des entiers positifs (ceux commençant par 0) : de 0000 à 0111
- et l’autre moitié sont des entiers strictement négatifs (ceux commençant par un 1) : de 1000 à 1111.
On peut donc représenter ainsi les entiers positifs compris entre 0 et 7 et les entiers strictement négatifs compris entre −8 et −1.
C’est-à-dire tous les entiers relatifs compris entre −8 et 7.
Il y en a bien $2^4=16$.
De manière générale, si on dispose de n bits pour représenter des entiers en complément à 2, on peut en représenter $2^n$.
La moitié d’entre eux sont des entiers positifs, il y en a $2^{n−1}$, et l’autre moitié des entiers strictement négatifs il y en a aussi $2^{n−1}$.
Ainsi, on peut représenter tous les entiers positifs compris entre 0 et $2^{n−1}−1$ et tous les entiers strictement négatifs compris entre $−2^{n−1}$ et −1, c’est-à-dire tous les entiers relatifs compris entre $−2^{n−1}$ et $2^{n−1}−1$.
d'où la propriété :
4) Au fait, pourquoi dit-on complément à 2 ?
Lorsque l’on cherche à déterminer le codage de −5, on cherche en fait le nombre k tel que k + 5 = 0
\begin{array}{c c c c c} \color{red}1& \color{red}1 & \color{red}1 & \color{red}1 & \ & 0 & 1 & 0 & 1 \
- & 1 & 0 & 1 & 1 \ \hline \color{red}1 & \color{blue}0 & \color{blue}0 & \color{blue}0 & \color{blue}0\ \end{array}
En binaire, le calcul de 5+(−5) est 0101 + 1011 qui donne 10000 c’est-à-dire $2^4$.
Cela signifie que 1011 est le complément à $2^4$ de 0101.
On devrait donc dire de manière plus rigoureuse le complément à $2^4$
Il n'y a pas un problème ? Je croyais que 5 + (−5) devait faire 0 et non $2^4$. En fait, en binaire le résultat donne 10000 mais comme on a choisi de coder sur 4 bits, le bit 1 n’est pas pris en compte (puisque c’est le 5ème bit) et le résultat en machine est donc bien égal à 0000, c’est-à-dire 0.
5) Voici une explication plus rigoureuse.
Notons k un entier positif et b son écriture binaire.
Cherchons l’opposé de b, c'est-à-dire le nombre m tel que b + m = 0
Notons $\overline{b}$ le nombre binaire dans lequel on inverse tous les bits de b.
on dit que $\overline{b}$ est le complément à 1 de b.
On remarque alors qu’on a toujours b + $\overline{b}$ = 1111 puisque pour chaque bit on additionne un bit 1 et un bit 0.
Par exemple, 1011 + 0100 = 1111.
Si on ajoute 1 à ce nombre 1111, on obtient 0, car on a choisi de coder sur 4 bits, on ignore la dernière retenue.
On vient de montrer que b + $\overline{b}$ + 1 = 0 et donc a trouvé la représentation binaire de notre nombre m = $\overline{b}$ +1.
Ainsi, pour représenter un entier négatif, on part de sa valeur absolue, que l’on code en binaire, puis on inverse tous les bits et enfin on ajoute 1.
Exercices
Exercice 1 :
En utilisant le complément à 2, représentez -15 en binaire (représentation sur 8 bits).
Exercice 2 :
En utilisant le complément à 2, représentez sur 8 bits l'entier 4 puis représentez, toujours sur 8 bits, l'entier -5.
Additionnez ces 2 nombres (en utilisant les représentations binaires bien évidemment), vérifiez que vous obtenez bien -1.
Exercice 3 :
Quel est l'entier relatif codé en complément à 2 sur un octet par le code 11011010 ?
Exercice 4 :
Quelles sont les bornes inférieure et supérieure d'un entier relatif codé sur 16 bits ?
1.3 - Nombres réels ✔
Représentation des données: types et valeurs de base
Représentation approximative des nombres réels : notion de nombre flottant
Capacités attendues :
Calculer sur quelques exemples la représentation de nombres réels : 0.1, 0.25 ou 1/3.
Commentaires :
0.2 + 0.1 n’est pas égal à 0.3.
Il faut éviter de tester l’égalité de deux flottants.
Aucune connaissance précise de la norme IEEE-754 n’est exigible.
1. Convertir un nombre binaire à virgule en décimal :
Exemples et Méthode :
$2.625_{10} = 2_10^0 + 6_10^{-1} + 2_10^{-2} + 5_10^{-3}$
$10.101_2 = 1_2^1 + 0_2^0 + 1_2^{-1} + 0_2^{-2} + 1*2^{-3}= 2 + 0 + 1/2^1 + 0 +1/2^3 = 2 + 0 + 0.5 +0 + 0.125 = 2.625_{10}$
def binary_to_decimal(binary_str):
# Séparation de la partie entière et fractionnaire
parts = binary_str.split('.')
integer_part = parts[0]
fractional_part = parts[1] if len(parts) > 1 else ""
# Conversion de la partie entière
decimal_integer = sum([int(bit) * (2 ** idx) for idx, bit in enumerate(integer_part[::-1])])
# Conversion de la partie fractionnaire
decimal_fractional = sum([int(bit) * (2 ** (-idx)) for idx, bit in enumerate(fractional_part, start=1)])
return decimal_integer + decimal_fractional
# Test
binary_str = input("Entrez un nombre binaire à virgule: ")
print(f"La représentation décimale de {binary_str} est: {binary_to_decimal(binary_str)}")
Entrez un nombre binaire à virgule: 10.101 La représentation décimale de 10.101 est: 2.625
def binary_to_decimal(binary_str):
# Séparation de la partie entière et fractionnaire
parts = binary_str.split('.')
integer_part = parts[0]
fractional_part = parts[1] if len(parts) > 1 else ""
# Conversion de la partie entière
decimal_integer = 0
print("Pour la partie entière:")
for idx, bit in enumerate(integer_part[::-1]):
value = int(bit) * (2 ** idx)
decimal_integer += value
print(f"{bit} × (2^ {idx}) = {value}")
print(f"La somme pour la partie entière est: {decimal_integer}\n")
# Conversion de la partie fractionnaire
decimal_fractional = 0
print("Pour la partie fractionnaire:")
for idx, bit in enumerate(fractional_part, start=1):
value = int(bit) * (2 ** (-idx))
decimal_fractional += value
print(f"{bit} × (2^ -{idx}) = {value}")
print(f"La somme pour la partie fractionnaire est: {decimal_fractional:}\n")
return decimal_integer + decimal_fractional
# Test
binary_str = input("Entrez un nombre binaire à virgule: ")
print(f"\nLa représentation décimale de {binary_str} est: {binary_to_decimal(binary_str)}")
Entrez un nombre binaire à virgule: 10.101 Pour la partie entière: 0 × (2^ 0) = 0 1 × (2^ 1) = 2 La somme pour la partie entière est: 2 Pour la partie fractionnaire: 1 × (2^ -1) = 0.5 0 × (2^ -2) = 0.0 1 × (2^ -3) = 0.125 La somme pour la partie fractionnaire est: 0.625 La représentation décimale de 10.101 est: 2.625
Exercice 1 : Conversion Binaire en Décimal
Convertir les nombres binaires suivants en décimal :
a) 101.11
b) 0.101
c) 1000.011
2. Conversion d'un nombre décimal à virgule en binaire
Voici les étapes pour convertir un nombre décimal à virgule en binaire :
Méthode :
Conversion de la partie entière:
- Divisez la partie entière du nombre décimal par 2.
- Notez le reste. Ce sera le bit le plus à droite (bit de poids le plus faible) du nombre binaire.
- Prenez le quotient de cette division et divisez-le à nouveau par 2.
- Notez le reste.
- Continuez cette procédure jusqu'à ce que le quotient soit égal à zéro.
Conversion de la partie fractionnaire:
- Multipliez la partie fractionnaire par 2.
- La partie entière du résultat est le bit suivant du nombre binaire (après la virgule).
- Ignorez la partie entière et gardez la partie fractionnaire.
- Multipliez à nouveau cette partie fractionnaire par 2.
- Continuez cette procédure jusqu'à ce que la partie fractionnaire devienne 0 ou jusqu'à ce que vous ayez suffisamment de bits pour obtenir la précision souhaitée.
Exemple :
Convertir $2.625_{10}$ en binaire.
Pour la partie entière $(2)$: $2÷2=12÷2=1$ avec un reste de $0$. C'est notre bit le plus à droite. $1÷2=01÷2=0$ avec un reste de $1$. C'est notre prochain bit. La partie entière en binaire est donc $10$.
Pour la partie fractionnaire $0.625$: $0.625×2=1.250.625×2=1.25$ => Premier bit après la virgule est $1$. On garde la partie fractionnaire 0.25. $0.25×2=0.50.25×2=0.5$ => Deuxième bit après la virgule est $0$. On garde la partie fractionnaire 0.5. $0.5×2=10.5×2=1$ => Troisième bit après la virgule est $1$. La partie fractionnaire est maintenant 0. La partie fractionnaire en binaire est donc $101$.
don $2.625_{10} = 10.101_2$.
from fractions import Fraction
def decimal_to_binary(n):
# Conversion de la partie entière
integer_part = int(n)
fractional_part = n - integer_part
# Convertir la partie entière en binaire
if integer_part == 0:
integer_binary = "0"
else:
integer_binary = bin(integer_part).split('b')[1]
print("Pour la partie entière " + str(integer_part) + ":")
temp = integer_part
while temp:
quotient = temp // 2
remainder = temp % 2
print(f"{temp}÷2 = {quotient} avec un reste de {remainder}.")
temp = quotient
print(f"La partie entière en binaire est donc {integer_binary}\n")
# Convertir la partie fractionnaire en fraction pour déterminer la répétition
fraction = Fraction(fractional_part).limit_denominator()
numerator = fraction.numerator
denominator = fraction.denominator
fractional_binary = ""
print(f"Pour la partie fractionnaire {fractional_part} :")
print(f"2*{fractional_part} = {2*fractional_part} ")
# Nous utiliserons cette liste pour stocker les numérateurs rencontrés
numerators = []
while numerator and numerator not in numerators:
numerators.append(numerator)
numerator *= 2
bit = numerator // denominator
print(f"{numerator/denominator} donc le bit après la virgule est {bit} , et on calcule 2*({numerator/denominator}-{bit}).")
fractional_binary += str(bit)
numerator %= denominator
# Si un numérateur est répété, alors il y a une répétition
if numerator:
idx_of_repeat = numerators.index(numerator)
non_repeating = fractional_binary[:idx_of_repeat]
repeating = fractional_binary[idx_of_repeat:]
fractional_binary = non_repeating + "[" + repeating + "]"
print(f"Répétition détectée : {repeating}")
print(f"La partie fractionnaire en binaire est donc {fractional_binary}.\n")
return integer_binary + "." + fractional_binary
# Test
number = float(input("Entrez un nombre décimal à virgule: "))
print()
print(f"\nLa représentation binaire de {number} est: {decimal_to_binary(number)}")
Entrez un nombre décimal à virgule: 2.625 Pour la partie entière 2: 2÷2 = 1 avec un reste de 0. 1÷2 = 0 avec un reste de 1. La partie entière en binaire est donc 10 Pour la partie fractionnaire 0.625 : 2*0.625 = 1.25 1.25 donc le bit après la virgule est 1 , et on calcule 2*(1.25-1). 0.5 donc le bit après la virgule est 0 , et on calcule 2*(0.5-0). 1.0 donc le bit après la virgule est 1 , et on calcule 2*(1.0-1). La partie fractionnaire en binaire est donc 101. La représentation binaire de 2.625 est: 10.101
Exercice 2 : Conversion Décimal à Binaire
Convertir les nombres décimaux suivants en binaire :
a) 5,75
b) 0,625
c) 8,375
d) 236,45
e) 0.1
f) 0.2
g) 0.3
f) 0.25
g) 1/3
réponse :
Remarques :
- Il est important de noter que certains nombres décimaux n'ont pas de représentation exacte en binaire, tout comme $1/3 = 0.[3]_{10}$ n'a pas de représentation exacte en base décimale. C'est le cas de $0.1_{10} = 0.0[0011]_2$.
- En programmation, en raison de l'imprécision (voir exemples ci-dessous), il est généralement déconseillé de vérifier l'égalité exacte de deux nombres flottants. À la place, les programmeurs vérifient souvent si la différence entre les deux est inférieure à un très petit nombre (parfois appelé "epsilon").
0.10.20.30.1+0.20.3-(0.1+0.2)3. La virgule flottante :
Imaginez que vous écriviez un très grand nombre, disons un milliard, comme 1,000,000,000.
C'est long, non ?
Au lieu de cela, on pourrait dire $1 x 10^9$.
Mais pourquoi flottante, pour les ordinateurs ?
Parce que la "virgule" (ou le "point" selon les régions) peut se "déplacer" (flotter) grâce à l'exposant.
Prenons un exemple : $123.45$ peut être écrit comme $1.2345 x 10^2$.
Comment les ordinateurs le voient :
Les ordinateurs décomposent ces nombres en trois parties:
- Signe : Le nombre est-il positif ou négatif?
- Exposant : Où est la virgule? (dans notre exemple, elle est déplacée de 2 places, donc $10^2$)
- Mantisse : Les chiffres du nombre (dans notre exemple, c'est 1.2345)
Pourquoi c'est compliqué : Les ordinateurs utilisent des bits pour représenter ces parties, et parfois ils doivent arrondir car ils n'ont pas assez de bits pour être précis. Sur un ordinateur 0.1 + 0.2 n'est pas exactement égal à 0.3.
Ceci n'est qu'une introduction de base à la virgule flottante. La compréhension complète du sujet nécessiterait une étude approfondie, en particulier des aspects mathématiques et des détails spécifiques de la norme IEEE 754.
1.4 - Expressions booléennes ✔
Représentation des données: types et valeurs de base
Valeurs booléennes: 0, 1. Opérateurs booléens: and, or, not.
Expressions booléennes
Compétences attendues :
Dresser la table d’une expression booléenne
Commentaires :
Le ou exclusif (xor) est évoqué.
Quelques applications directes comme l’addition binaire sont présentées.
L’attention des élèves est attirée sur le caractère séquentiel de certains opérateurs booléens.
1. Valeurs booléennes
En informatique et en logique, une valeur booléenne peut prendre deux valeurs possibles :
- 0 : généralement interprété comme faux
- 1 : généralement interprété comme vrai
2. Opérateurs booléens
Il y a trois opérateurs booléens principaux : and, or, et not.
a. AND
L'opérateur and retourne 1 si les deux opérandes sont 1. Sinon, il retourne 0.
| A | B | A and B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
b. OR
L'opérateur or retourne 1 si au moins un des opérandes est 1. Sinon, il retourne 0.
| A | B | A or B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
c. NOT
L'opérateur not inverse la valeur booléenne.
| A | not A |
|---|---|
| 0 | 1 |
| 1 | 0 |
d. XOR (OU exclusif)
L'opérateur xor retourne 1 si exactement un des opérandes est 1. Si les deux opérandes sont identiques, il retourne 0.
| A | B | A xor B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
3. Expressions booléennes
Une expression booléenne est une combinaison de valeurs booléennes et d'opérateurs.
Exercice : Table de vérité de A and (B or C)
Complétez la table de vérité ci-dessous :
| A | B | C | B or C | A and (B or C) |
|---|---|---|---|---|
| 0 | 0 | 0 | ||
| 0 | 0 | 1 | ||
| 0 | 1 | 0 | ||
| 0 | 1 | 1 | ||
| 1 | 0 | 0 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 0 | ||
| 1 | 1 | 1 |
Solution : Table de vérité de A and (B or C)
| A | B | C | B or C | A and (B or C) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
print("A", "B", "C", "A and (B or C)", sep="\t")
print("-" * 5 * 8) # Pour ajouter une ligne de séparation (5 colonnes * 8 caractères par colonne)
for A in [False, True]:
for B in [False, True]:
for C in [False, True]:
print(int(A), int(B), int(C), int(A and (B or C)), sep="\t")A B C A and (B or C) ---------------------------------------- 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1
print("A", "B", "C", "A and B", "A and C", "(A and B) or (A and C)", sep="\t")
print("-" * 7 * 8) # Pour ajouter une ligne de séparation (7 colonnes * 8 caractères par colonne)
for A in [False, True]:
for B in [False, True]:
for C in [False, True]:
print(int(A), int(B), int(C), int(A and B), int(A and C), int((A and B) or (A and C)), sep="\t")
A B C A and B A and C (A and B) or (A and C) -------------------------------------------------------- 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 0 1 1 1 1 0 1 0 1 1 1 1 1 1 1
Conclusion :
A and (B or C) = (A and B) or (A and C)
Les autres identitées booléennes peuvent se démontrer de la même façon, ou sinon avec des tables de vérités.
Identités Booléennes :
- Commutativité:
- A and B = B and A
- A or B = B or A
- Lois du neutre :
- A and False = False
- A or True = True
- Idempotence :
- A and A = A
- A or A = A
- Double négation :
- not (not A) = A
- Distribution :
- A and (B or C) = (A and B) or (A and C)
- A or (B and C) = (A or B) and (A or C)
- Associativité :
- A and (B and C) = (A and B) and C
- A or (B or C) = (A or B) or C
4. Commentaires :
Applications directes comme l’addition binaire :
L'addition binaire est un exemple où les opérateurs booléens sont directement appliqués. Lors de l'addition de deux bits A et B avec une retenue entrante Rin :
-
le bit résultant de l'addition des deux bits d'entrée et de la retenue entrante. S=A xor B xor RinS=A xor B xor Rin
-
la retenue sortante (Rout) :Elle est générée si deux des trois entrées (A, B et Rin) ou plus sont égales à 1. Rout=(A and B) or (Rin and (A xor B))
Caractère séquentiel de certains opérateurs booléens :
Certains opérateurs, comme and et or, sont souvent évalués de manière séquentielle. Par exemple, en programmation, si le premier opérande de and est faux, le second n'est souvent même pas évalué car le résultat global sera de toute façon faux. De même, pour or, si le premier opérande est vrai, le résultat global est vrai sans même évaluer le second opérande. C'est ce qu'on appelle l'évaluation "court-circuit".
Exercices
Exercice 1: Tables de Vérité
Établissez les tables de vérité pour les opérations suivantes :
a. A and B
b. A or B
c. not A
Correction :
a. A and B :
| A | B | A and B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
b. A or B :
| A | B | A or B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
c. not A :
| A | not A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Exercice 2: Analyse d'Expressions
Determinez si les expressions booléennes suivantes sont toujours vraies, toujours fausses, ou dépendent des valeurs de A et B :
a. A or not A
b. A and not A
c. A or (A and B)
Correction :
a. A or not A: Toujours vrai
b. A and not A: Toujours faux
c. A or (A and B): Équivalent à A, donc dépend de la valeur de A.
Exercice 3: Expressions Combinées
Évaluez les expressions booléennes suivantes pour toutes les combinaisons possibles de A, B, et C :
a. (A and B) or C
b. A and (B or C)
c. not A and (B or not C)
Correction :
a. (A and B) or C :
| A | B | C | A and B | (A and B) or C |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
b. A and (B or C) :
| A | B | C | B or C | A and (B or C) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
c. not A and (B or not C) :
| A | B | C | not A | not C | B or not C | not A and (B or not C) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 |
1.5 - ASCII, ISO, Unicode ✔
Représentation des données: types et valeurs de base
Représentation d’un texte en machine.
Exemples des encodages ASCII, ISO-8859-1,Unicode
Compétences attendues :
Identifier l’intérêt des différentssystèmes d’encodage.
Convertir un fichier texte dans différents formats d’encodage.
Commentaires :
Aucune connaissance précise desnormes d’encodage n’est exigible.
Un ordinateur ne comprend que des nombres, et donc, pour traiter du texte, il doit le convertir en nombres. C'est là qu'interviennent les systèmes d'encodage.
Exemples des encodages:
1. ASCII (American Standard Code for Information Interchange):
- Utilise 7 bits pour représenter un caractère.
- Peut représenter 128 caractères différents (0 à 127).
- Se limite principalement aux lettres, chiffres et symboles couramment utilisés en anglais.
# Ce programme affiche les 128 caractères ASCII et leurs valeurs numériques correspondantes.
def afficher_ascii():
for i in range(128):
print(f"{i:3} - {chr(i)}")
afficher_ascii() 0 -
1 -
2 -
3 -
4 -
5 -
6 -
7 -
8 -
9 -
10 -
11 -
12 -
13 -
14 -
15 -
16 -
17 -
18 -
19 -
20 -
21 -
22 -
23 -
24 -
25 -
26 -
27 -
28 -
29 -
30 -
31 -
32 -
33 - !
34 - "
35 - #
36 - $
37 - %
38 - &
39 - '
40 - (
41 - )
42 - *
43 - +
44 - ,
45 - -
46 - .
47 - /
48 - 0
49 - 1
50 - 2
51 - 3
52 - 4
53 - 5
54 - 6
55 - 7
56 - 8
57 - 9
58 - :
59 - ;
60 - <
61 - =
62 - >
63 - ?
64 - @
65 - A
66 - B
67 - C
68 - D
69 - E
70 - F
71 - G
72 - H
73 - I
74 - J
75 - K
76 - L
77 - M
78 - N
79 - O
80 - P
81 - Q
82 - R
83 - S
84 - T
85 - U
86 - V
87 - W
88 - X
89 - Y
90 - Z
91 - [
92 - \
93 - ]
94 - ^
95 - _
96 - `
97 - a
98 - b
99 - c
100 - d
101 - e
102 - f
103 - g
104 - h
105 - i
106 - j
107 - k
108 - l
109 - m
110 - n
111 - o
112 - p
113 - q
114 - r
115 - s
116 - t
117 - u
118 - v
119 - w
120 - x
121 - y
122 - z
123 - {
124 - |
125 - }
126 - ~
127 -
2. ISO-8859-1 (aussi appelé Latin-1):
- Extension de l'ASCII.
- Utilise 8 bits pour représenter un caractère.
- Peut représenter 256 caractères différents.
- Conçu pour couvrir la majorité des langues occidentales.
#Ce programme affiche les 256 caractères de l'encodage Latin-1 et leurs valeurs numériques correspondantes.
# Notez que les premiers 128 caractères seront les mêmes qu'ASCII.
def afficher_latin1():
for i in range(256):
print(f"{i:3} - {chr(i)}")
afficher_latin1() 0 -
1 -
2 -
3 -
4 -
5 -
6 -
7 -
8 -
9 -
10 -
11 -
12 -
13 -
14 -
15 -
16 -
17 -
18 -
19 -
20 -
21 -
22 -
23 -
24 -
25 -
26 -
27 -
28 -
29 -
30 -
31 -
32 -
33 - !
34 - "
35 - #
36 - $
37 - %
38 - &
39 - '
40 - (
41 - )
42 - *
43 - +
44 - ,
45 - -
46 - .
47 - /
48 - 0
49 - 1
50 - 2
51 - 3
52 - 4
53 - 5
54 - 6
55 - 7
56 - 8
57 - 9
58 - :
59 - ;
60 - <
61 - =
62 - >
63 - ?
64 - @
65 - A
66 - B
67 - C
68 - D
69 - E
70 - F
71 - G
72 - H
73 - I
74 - J
75 - K
76 - L
77 - M
78 - N
79 - O
80 - P
81 - Q
82 - R
83 - S
84 - T
85 - U
86 - V
87 - W
88 - X
89 - Y
90 - Z
91 - [
92 - \
93 - ]
94 - ^
95 - _
96 - `
97 - a
98 - b
99 - c
100 - d
101 - e
102 - f
103 - g
104 - h
105 - i
106 - j
107 - k
108 - l
109 - m
110 - n
111 - o
112 - p
113 - q
114 - r
115 - s
116 - t
117 - u
118 - v
119 - w
120 - x
121 - y
122 - z
123 - {
124 - |
125 - }
126 - ~
127 -
128 -
129 -
130 -
131 -
132 -
133 -
134 -
135 -
136 -
137 -
138 -
139 -
140 -
141 -
142 -
143 -
144 -
145 -
146 -
147 -
148 -
149 -
150 -
151 -
152 -
153 -
154 -
155 -
156 -
157 -
158 -
159 -
160 -
161 - ¡
162 - ¢
163 - £
164 - ¤
165 - ¥
166 - ¦
167 - §
168 - ¨
169 - ©
170 - ª
171 - «
172 - ¬
173 -
174 - ®
175 - ¯
176 - °
177 - ±
178 - ²
179 - ³
180 - ´
181 - µ
182 - ¶
183 - ·
184 - ¸
185 - ¹
186 - º
187 - »
188 - ¼
189 - ½
190 - ¾
191 - ¿
192 - À
193 - Á
194 - Â
195 - Ã
196 - Ä
197 - Å
198 - Æ
199 - Ç
200 - È
201 - É
202 - Ê
203 - Ë
204 - Ì
205 - Í
206 - Î
207 - Ï
208 - Ð
209 - Ñ
210 - Ò
211 - Ó
212 - Ô
213 - Õ
214 - Ö
215 - ×
216 - Ø
217 - Ù
218 - Ú
219 - Û
220 - Ü
221 - Ý
222 - Þ
223 - ß
224 - à
225 - á
226 - â
227 - ã
228 - ä
229 - å
230 - æ
231 - ç
232 - è
233 - é
234 - ê
235 - ë
236 - ì
237 - í
238 - î
239 - ï
240 - ð
241 - ñ
242 - ò
243 - ó
244 - ô
245 - õ
246 - ö
247 - ÷
248 - ø
249 - ù
250 - ú
251 - û
252 - ü
253 - ý
254 - þ
255 - ÿ
3. Unicode:
- Conçu pour représenter presque tous les caractères de toutes les langues écrites dans le monde.
- UTF-8, UTF-16 et UTF-32 sont des méthodes courantes pour encoder des données en Unicode.
- UTF-8 est devenu la méthode d'encodage la plus populaire sur le web.
# Ce programme utilise UTF-8 pour afficher quelques caractères Unicode sélectionnés provenant de différents scripts :
# comme le cyrillique, le grec, le hiragana japonais et le chinois).
#Il affiche la valeur numérique de chaque caractère ainsi que le caractère lui-même.
def afficher_utf8():
exemples_unicode = ["\u00E9", "\u0420", "\u03B1", "\u304A", "\u4E00"]
for caractere in exemples_unicode:
print(f"{ord(caractere):5} - {caractere}")
afficher_utf8()233 - é 1056 - Р 945 - α 12362 - お 19968 - 一
4. Intérêt des différents systèmes d’encodage:
- ASCII est simple et suffisant pour les textes en anglais.
- ISO-8859-1 offre une plus grande variété de caractères pour les langues occidentales.
- Unicode est universel et peut représenter presque toutes les langues du monde.
5. Convertir un fichier texte dans différents formats d’encodage:
Des outils comme Notepad++ ou des commandes Unix comme iconv peuvent être utilisés pour convertir des fichiers d'un format d'encodage à un autre.
Notepad++: Si vous utilisez Notepad++:
- Ouvrez votre fichier avec Notepad++.
- Dans la barre de menu, cliquez sur "Encodage".
- Pour convertir, par exemple, en UTF-8, choisissez "Convertir en UTF-8".
- Enregistrez le fichier.
Commande iconv (Unix):
Si vous êtes sur un système Unix (comme Linux ou macOS), vous pouvez utiliser iconv pour convertir un fichier.
Pour convertir un fichier texte de ISO-8859-1 à UTF-8:
iconv -f ISO-8859-1 -t UTF-8 input.txt -o output.txt
Dans cet exemple:
-fspécifie l'encodage source.-tspécifie l'encodage cible.input.txtest le fichier source.output.txtest le fichier de sortie.
Python: Python offre une manière programmatique de convertir un encodage de fichier. Voici un exemple simple:
def convert_encoding(input_file, output_file, from_encoding, to_encoding):
with open(input_file, 'r', encoding=from_encoding) as source_file:
content = source_file.read()
with open(output_file, 'w', encoding=to_encoding) as target_file:
target_file.write(content)
convert_encoding('input.txt', 'output.txt', 'ISO-8859-1', 'UTF-8')2.1 - p-uplets ✔
Représentation des données: types construits
p-uplets, p-uplets nommés
Compétence exigible : Écrire une fonction renvoyant un p-uplet de valeurs
1. Les ( p )-uplets
Définition
Un ( p )-uplet est une collection ordonnée de ( p ) éléments. C'est un concept généralisé des couples (2 éléments), triplets (3 éléments), etc.
mon_tuple = (1, "deux", 3.0, "quatre")
print(mon_tuple)
print(mon_tuple[1])(1, 'deux', 3.0, 'quatre') deux
Caractéristiques des ( p )-uplets
Les ( p )-uplets, ou simplement tuples en Python, possèdent plusieurs caractéristiques distinctives :
Ordonné :
L'ordre des éléments dans un ( p )-uplet est fixe. Cela signifie que les éléments ont une position déterminée qui ne change pas.
Immuabilité :
Une fois qu'un ( p )-uplet est défini, il ne peut pas être modifié.
Cela implique que :
- Les éléments ne peuvent pas être changés.
- Aucun élément ne peut être ajouté.
- Aucun élément ne peut être supprimé. Cette immuabilité est une différence fondamentale par rapport aux listes en Python, qui sont modifiables.
Exemples :
- Un triplet représentant les dimensions d'une boîte : (5cm, 10cm, 3cm)
dimensions_boite = (5, 10, 3) # en cm
longueur, largeur, hauteur = dimensions_boite
print(f"Volume boîte = {longueur*largeur*hauteur} cm3")Volume boîte = 150 cm3
- Distance dans un espace 2D :
La distance entre deux points $A(x_A, y_A)$ et $B(x_B, y_B)$ sur un plan dans un repère orthonormée est donnée par :
$\text{AB} = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} $
import math
def distance_entre_points(A, B):
xA, yA = A
xB, yB = B
return math.sqrt((xB - xA)**2 + (yB - yA)**2)
point1 = (3, 5)
point2 = (6, 9)
print(f"Distance entre {point1} et {point2} = {distance_entre_points(point1, point2):.2f}")- Pile ou Face :
import random
def lancer_piece():
return "Pile" if random.randint(0, 1) == 0 else "Face"
# Simuler le lancer d'une pièce \( n \) fois
n = 20
resultats = tuple(lancer_piece() for _ in range(n))
print(f"Résultats : {resultats}")
# Calculer la fréquence de chaque résultat
frequences = {
"Pile": resultats.count("Pile") / n,
"Face": resultats.count("Face") / n
}
print(f"Fréquence de 'Pile' après {n} lancers : {frequences['Pile']:.2f}")
print(f"Fréquence de 'Face' après {n} lancers : {frequences['Face']:.2f}")- fonction renvoyant un p-uplet de valeurs
Attention : Compétence exigible
def obtenir_details():
nom = "Alice"
age = 30
profession = "Ingénieur"
return (nom, age, profession)
details = obtenir_details()
print(details) # Affiche: ('Alice', 30, 'Ingénieur')
def obtenir_details():
nom = "Alice"
age = 30
profession = "Ingénieur"
return (nom, age, profession)
nom, age, profession = obtenir_details()
print(nom)
print(age)
print(profession) 2. Les ( p )-uplets només
Définition
Un ( p )-uplet nommé est similaire à un ( p )-uplet, mais chaque élément a un nom ou une clé associée. C'est comme un dictionnaire avec ( p ) entrées.
Exemples
- Un couple nommé pour les coordonnées d'un point : {'x': 3, 'y': 5}
- Un triplet nommé pour une date : {'day': 10, 'month': 'April', 'year': 2023}
- Un quadruplet nommé pour des informations personnelles : {'name': 'Alice', 'age': 30, 'city': 'Paris', 'profession': 'Engineer'}
Caractéristiques des ( p )-uplets nommés
Ordonné: Les éléments ont un ordre fixe.
Accès par nom: On accède aux éléments par leur nom.
Immuabilité : Ils ne peuvent pas être modifiés une fois créés.
Types variés: Ils peuvent contenir différents types (int, str, etc.).
Lisibilité: Le code est plus clair avec des noms pour chaque élément.
Usage: Utiles pour des données structurées.
Exemples
- Dictionnaire :
# Création du dictionnaire de traduction
traduction = {
'hello': 'bonjour',
'goodbye': 'au revoir',
'please': "s'il vous plaît",
'thank you': 'merci'
}
print(traduction['hello'])- Notes :
# Création des notes pour Alice en NSI
notes_nsi_alice = {
"DS1": 85,
"DS2": 87,
"DM": 90
}
# Création du dictionnaire pour Alice
alice = {
"Nom": "Alice",
"Age": 16,
"NSI": notes_nsi_alice
}
# Accès à la note de Alice pour le DS1 en NSI
age = alice['Age']
note_ds1_nsi = alice["NSI"]["DS1"]
print(f"Alice a {age} ans.")
print(f"La note d'Alice pour le DS1 en NSI est : {note_ds1_nsi}/100.")Exercices avancés sur les ( p )-uplets et ( p )-uplets nommés
Exercice 1 : Conversion
liste_dicts =[{ "nom": "Alice", "âge": 30 }, { "nom": "Bob", "âge": 25 }]
Convertissez cette liste de dictionnaires en une liste de tuples.
liste_dicts = [{ "nom": "Alice", "âge": 30 }, { "nom": "Bob", "âge": 25 }]
liste_tuples = [(d["nom"], d["âge"]) for d in liste_dicts]
print(liste_tuples)
Exercice 2 : Recherche avancée
produits = [("Ordinateur", "Un appareil pour le traitement de l'information"), ("Voiture", "Un moyen de transport terrestre"), ("Avion", "Un moyen de transport aérien")]
Écrivez une fonction qui recherche le mot "transport" et renvoie les noms des produits correspondants.
produits = [("Ordinateur", "Un appareil pour le traitement de l'information"),
("Voiture", "Un moyen de transport terrestre"),
("Avion", "Un moyen de transport aérien")]
resultats = [p[0] for p in produits if "transport" in p[1]]
print(resultats)Exercice 3 : Fusion
Noms = ["Alice", "Bob", "Charlie"], Notes = [85, 90, 88]
Fusionnez ces deux listes pour obtenir une liste de tuples.
noms = ["Alice", "Bob", "Charlie"]
notes = [85, 90, 88]
fusion = [(noms[i], notes[i]) for i in range(len(noms))]
print(fusion)Exercice 4 : Dictionnaires de tuples
étudiants = {"Alice": (85, 88, 90), "Bob": (80, 78, 92), "Charlie": (78, 77, 85)}
Calculez la moyenne de chaque étudiant et stockez-la dans un nouveau dictionnaire.
étudiants = {"Alice": (85, 88, 90), "Bob": (80, 78, 92), "Charlie": (78, 77, 85)}
moyennes = {nom: sum(notes)/len(notes) for nom, notes in étudiants.items()}
print(moyennes)2.2 - Tableau ✔
Représentation des données : types construits
Tableau indexé, tableau donné en compréhension
Capacités attendues :
- Lire et modifier les éléments d’un tableau grâce à leurs index.
- Construire un tableau par compréhension.
- Utiliser des tableaux de tableaux pour représenter des matrices : notation a[i][j].
- Itérer sur les éléments d’un tableau.
Commentaires :
- Seuls les tableaux dont les éléments sont du même type sont présentés.
- Aucune connaissance des tranches (slices) n’est exigible.
- L’aspect dynamique des tableaux de Python n’est pas évoqué.
- Python identifie listes et tableaux.
- Il n’est pas fait référence aux tableaux de la bibliothèque NumPy.
En Python, les tableaux sont indexés, ce qui signifie que chaque élément a un index numérique commençant à 0. Pour lire un élément, On utilise l'index entre crochets :
mon_tableau = [10, 20, 30, 40]
print(mon_tableau)
print(mon_tableau[0])
print(mon_tableau[1])
print(mon_tableau[-1])
print(mon_tableau[-3])
print(type(mon_tableau))[10, 20, 30, 40] 10 20 40 20 <class 'list'>
Pour modifier un élément, utilisez également l'index :
mon_tableau = [10, 20, 30, 40]
print(mon_tableau)
mon_tableau[2] = 35
print(mon_tableau) [10, 20, 30, 40] [10, 20, 35, 40]
Pour connaître le nombre éléments d’une liste, on dispose de la fonction len().
mon_tableau = [10, 20, 30, 40]
print(mon_tableau)
print(len(mon_tableau))[10, 20, 30, 40] 4
Il est possible de ne sélectionner qu’une partie du tableau.
mon_tableau = [10, 20, 30, 40]
print(mon_tableau[1:3])
print(mon_tableau[1:])
print(mon_tableau[:3])[20, 30] [20, 30, 40] [10, 20, 30] 20
Il est possible d’ajouter des éléments à la fin d’une liste avec la fonction append().
mon_tableau = [10, 20, 30, 40]
mon_tableau.append(50)
print(mon_tableau)[10, 20, 30, 40, 50]
Il est possible de supprimer des éléments d’une liste avec la fonction pop().
mon_tableau = [10, 20, 30, 40]
mon_tableau.pop(1)
print(mon_tableau)[10, 30, 40]
mon_tableau = [10, 20, 30, 40]
mon_tableau.pop()
print(mon_tableau)[10, 20, 30]
Tableau Donné en Compréhension
Vous pouvez construire des tableaux en utilisant la "compréhension de liste", qui est une manière concise de créer des listes :
list(range(0,50,4))puissances = [2 ** n for n in range(32)]
print(puissances)[1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456, 536870912, 1073741824, 2147483648]
dix_zeros = [0]*10
print(dix_zeros)[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Utilisation de Tableaux de Tableaux
Pour représenter une matrice, vous pouvez utiliser un tableau de tableaux :
matrice = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
print(matrice)
print(matrice[0][0])
print(matrice[1][2])
print(type(mon_tableau))
print("Nombre de lignes dans la matrice :", len(matrice))
print("Taille de la matrice (lignes x colonnes) :", len(matrice), "x", len(matrice[0]))
# Modifier un élément de la matrice
matrice[1][1] = 100
print(matrice)[[1, 2, 3], [4, 5, 6], [7, 8, 9]] 1 6 <class 'list'> Nombre de lignes dans la matrice : 3 Taille de la matrice (lignes x colonnes) : 3 x 3 [[1, 2, 3], [4, 100, 6], [7, 8, 9]]
matrice_de_zeros = [[0 for _ in range(3)] for _ in range(3)]
print(matrice_de_zeros)[[0, 0, 0], [0, 0, 0], [0, 0, 0]]
matrice_multiplication = [[i * j for j in range(11)] for i in range(11)]
print(matrice_multiplication)[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], [0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20], [0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30], [0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40], [0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50], [0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60], [0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70], [0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80], [0, 9, 18, 27, 36, 45, 54, 63, 72, 81, 90], [0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100]]
Itérer sur les Éléments d'un Tableau
Utilisez une boucle for pour parcourir tous les éléments d'un tableau :
mon_tableau = [10, 20, 30, 40]
for élément in mon_tableau:
print(élément)10 20 30 40
Ou avec index :
mon_tableau = [10, 20, 30, 40]
for i in range(len(mon_tableau)):
print(mon_tableau[i])10 20 30 40
matrice = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
for i in range(3):
for j in range(3):
print(matrice[i][j])
print()1 2 3 4 5 6 7 8 9
matrice_multiplication = [[i * j for j in range(11)] for i in range(11)]
# Afficher la matrice
for ligne in matrice_multiplication:
print(ligne)[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] [0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20] [0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30] [0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40] [0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50] [0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60] [0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70] [0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80] [0, 9, 18, 27, 36, 45, 54, 63, 72, 81, 90] [0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
2.3 - Dictionnaire ✔
Structures de données
Dictionnaires par clés et valeurs
Capacités attendus :
Construire une entrée de dictionnaire.
Itérer sur les éléments d’un dictionnaire.
Commentaires :
Il est possible de présenter les données EXIF d’une image sous la forme d’un enregistrement.
En Python, les p-uplets nommés sont implémentés par des dictionnaires.
Utiliser les méthodes keys(),values () et items ().
1) Dictionnaires
Un dictionnaire est une structure de données qui stocke des paires clé-valeur.
Chaque clé est unique et chaque clé est associée à une valeur.
Voici comment vous pouvez créer un dictionnaire en Python :
mon_dictionnaire = {
"nom": "Alice",
"age": 30,
"email": "alice@email.com"
}
print(mon_dictionnaire){'nom': 'Alice', 'age': 30, 'email': 'alice@email.com'}
un_autre_dictionnaire = dict(nom='Bob', age=40, email='bob@email.com')
print(un_autre_dictionnaire){'nom': 'Bob', 'age': 40, 'email': 'bob@email.com'}
Pour accéder aux valeurs en utilisant leurs clés correspondantes :
print(mon_dictionnaire["nom"])
print(mon_dictionnaire["age"]) Alice 30
Pour modifier les valeurs associées aux clés :
mon_dictionnaire["age"] = 31
print(mon_dictionnaire["age"]) 31
Pour ajouter de nouvelles paires clé-valeur au dictionnaire :
mon_dictionnaire["adresse"] = "123 rue du Paradis"
print(mon_dictionnaire){'nom': 'Alice', 'age': 31, 'email': 'alice@email.com', 'adresse': '123 rue du Paradis'}
Pour supprimer une paire clé-valeur, utilisez le mot-clé del :
del mon_dictionnaire["adresse"]
print(mon_dictionnaire){'nom': 'Alice', 'age': 31, 'email': 'alice@email.com'}
Pour afficher la taille d'un dictionnaire :
print(len(mon_dictionnaire))3
Itérer sur les clés
for cle in mon_dictionnaire:
print(cle)nom age email
autre méthode :
cles = mon_dictionnaire.keys()
print(cles)
# Pour convertir en liste
liste_cles = list(cles)
print(liste_cles) dict_keys(['nom', 'age', 'email']) ['nom', 'age', 'email']
Itérer sur les valeurs
for valeur in mon_dictionnaire.values():
print(valeur)Alice 31 alice@email.com
autre méthode :
valeurs = mon_dictionnaire.values()
print(valeurs)
# Pour convertir en liste
liste_valeurs = list(valeurs)
print(liste_valeurs) dict_values(['Alice', 31, 'alice@email.com']) ['Alice', 31, 'alice@email.com']
Itérer sur les clés et les valeurs
for cle, valeur in mon_dictionnaire.items():
print(f"{cle} : {valeur}")nom : Alice age : 30 email : alice@email.com
Pour rechercher une valeur dans un dictionnaire en Python
"Alice" in mon_dictionnaire.values()valeur_recherchée = "Alice"
for valeur in mon_dictionnaire.values():
if valeur == valeur_recherchée:
print(f"La valeur '{valeur_recherchée}' a été trouvée dans le dictionnaire.")
breakLa valeur 'Alice' a été trouvée dans le dictionnaire.
autre méthode :valeur_recherchée = "Alice"
for cle, valeur in mon_dictionnaire.items():
if valeur == valeur_recherchée:
print(f"La valeur '{valeur_recherchée}' a été trouvée dans le dictionnaire avec la clé '{cle}'.")
break
La valeur 'Alice' a été trouvée dans le dictionnaire avec la clé 'nom'.
2) Index
L'index est un autre concept en programmation, généralement associé aux tableaux ou aux listes.
Une liste est une collection ordonnée d'éléments, qui peut contenir des données de types différents.
Contrairement aux dictionnaires, les éléments d'un tableau sont accessibles par leur position, ou index, qui commence généralement par 0.
ma_liste = ['Alice', 31, 'alice@email.com', 'adresse']
print(ma_liste[0])
print(ma_liste[1])
print(ma_liste[-1])
print(ma_liste[-2])
print(ma_liste[1:]) # Afficher la liste à partir de l'indice 1
print(ma_liste[1:3]) # Afficher la liste à partir de l'indice 1 à 2 !!!
print(ma_liste[:-1]) # Afficher la liste sauf le dernierAlice 31 adresse alice@email.com [31, 'alice@email.com', 'adresse'] [31, 'alice@email.com'] ['Alice', 31, 'alice@email.com']
Pour changer une valeur dans la liste, assignez une nouvelle valeur à l'index correspondant.
ma_liste[0] = 10
print(ma_liste)[10, 31, 'alice@email.com', 'adresse']
Pour afficher la taille d'une liste :
print(len(mon_liste))Pour rechercher une valeur dans une liste en Python
'alice@email.com' in ma_listeautre méthode :
valeur_recherchée = 'alice@email.com'
for i, valeur in enumerate(ma_liste):
if valeur == valeur_recherchée:
print(f"La valeur {valeur_recherchée} est trouvée à l'indice {i}.")
breakLa valeur alice@email.com est trouvée à l'indice 2.
3) Différence entre clés et index
La principale différence entre les clés d'un dictionnaire et les index d'une liste est que les clés sont généralement des chaînes de caractères qui représentent le sens sémantique des valeurs, tandis que les index sont des entiers qui représentent la position des valeurs dans la liste.
4) P-uplets nommés
En Python, les p-uplets nommés peuvent être implémentés par des dictionnaires ou par collections.namedtuple.
personnes = {
'Alice': {'age': 30, 'email': 'alice@email.com'},
'Bob': {'age': 40, 'email': 'bob@email.com'},
'Charlie': {'age': 50, 'email': 'charlie@email.com'}
}
print(personnes['Alice'])
print(personnes['Alice']['age']){'age': 30, 'email': 'alice@email.com'}
30
from collections import namedtuple
# Définition du p-uplet nommé
Personne = namedtuple('Personne', ['nom', 'age', 'email'])
# Création d'une instance du p-uplet nommé
alice = Personne(nom='Alice', age=30, email='alice@email.com')
bob = Personne(nom='Bob', age=40, email='bob@email.com')
charlie = Personne(nom='Charlie', age=50, email='charlie@email.com')
print(alice)
print(alice.nom)
print(alice.age)Personne(nom='Alice', age=30, email='alice@email.com') Alice 30
Les données EXIF d'une image
Les données EXIF (Exchangeable Image File Format) d'une image peuvent être représentées sous forme de dictionnaire.
Par exemple, pour lire les données EXIF d'une image, on utilise la bibliothèque PIL.
Télécharger l'image ci-dessus est collée importe là dans ce fichier basthon
from PIL import Image
image = Image.open("Pieds_du_femme_dans_le_metro.jpg")
exif_data = image._getexif()
print(exif_data){34853: {0: b'\x02\x02\x00\x00', 1: 'N', 2: (41.0, 24.0, 9.66), 3: 'E', 4: (2.0, 9.0, 9.9), 18: 'WGS-84'}, 296: 2, 34665: 202, 271: 'Sony', 272: 'G8441', 305: '47.1.A.16.20_0_a600', 274: 1, 306: '2018:10:25 09:07:03', 282: 72.0, 283: 72.0, 36864: b'0231', 37121: b'\x01\x02\x03\x00', 37377: 5.64, 36867: '2018:10:25 09:07:03', 36868: '2018:10:25 09:07:03', 37380: 0.0, 40960: b'0100', 37383: 5, 37384: 0, 37385: 16, 37386: 4.4, 40961: 1, 40962: 1024, 41988: 1.0, 41990: 0, 41996: 0, 37520: '991195', 37521: '991195', 37522: '991195', 40963: 576, 33434: 0.02, 33437: 2.0, 41985: 0, 34855: 500, 41986: 0, 41987: 0}
for cle, valeur in exif_data.items():
print(f"{cle} : {valeur}")34853 : {0: b'\x02\x02\x00\x00', 1: 'N', 2: (41.0, 24.0, 9.66), 3: 'E', 4: (2.0, 9.0, 9.9), 18: 'WGS-84'}
296 : 2
34665 : 202
271 : Sony
272 : G8441
305 : 47.1.A.16.20_0_a600
274 : 1
306 : 2018:10:25 09:07:03
282 : 72.0
283 : 72.0
36864 : b'0231'
37121 : b'\x01\x02\x03\x00'
37377 : 5.64
36867 : 2018:10:25 09:07:03
36868 : 2018:10:25 09:07:03
37380 : 0.0
40960 : b'0100'
37383 : 5
37384 : 0
37385 : 16
37386 : 4.4
40961 : 1
40962 : 1024
41988 : 1.0
41990 : 0
41996 : 0
37520 : 991195
37521 : 991195
37522 : 991195
40963 : 576
33434 : 0.02
33437 : 2.0
41985 : 0
34855 : 500
41986 : 0
41987 : 0
exif_data[34853]exif_data[34853][1],exif_data[34853][2],exif_data[34853][3],exif_data[34853][4]3.1 - CSV Indexation ✔
Traitement de données en tables
Indexation de tables
Capacités attendus :
Importer une table depuis un fichier texte tabulé ou un fichier CSV.
Commentaires :
Est utilisé un tableau doublement indexé ou un tableau de p-uplets qui partagent les mêmes descripteurs.
Données et txt
Voici un exemple de programmes Python qui prend en entrée des données, les sauvegarde dans un fichier txt, puis les modifie.
Maintenant le txt peut être créé directement par un logiciel comme Bloc-notes.
def sauvegarde_texte(file, donnees):
with open(file, 'w') as fichier:
for ligne in donnees:
fichier.write(','.join(ligne) + '\n')
print(f"Données sauvegardées dans {file} !")
def import_texte(file):
donnees = []
with open(file, 'r') as fichier:
for ligne in fichier:
donnees.append(ligne.strip().split(','))
return donnees
donnees = [
['nom', 'age', 'taille'],
['Alice', '30', '1.65'],
['Bob', '25', '1.75'],
['Charlie', '28', '1.80']
]
sauvegarde_texte('donnees.txt', donnees)
print(import_texte('donnees.txt'))Données sauvegardées dans donnees.txt ! [['nom', 'age', 'taille'], ['Alice', '30', '1.65'], ['Bob', '25', '1.75'], ['Charlie', '28', '1.80']]
print(donnees)
donnees[2][0] = "Bob L'éponge"
print(donnees)
sauvegarde_texte('donnees.txt',donnees)
print(import_texte('donnees.txt'))[['nom', 'age', 'taille'], ['Alice', '30', '1.65'], ['Bob', '25', '1.75'], ['Charlie', '28', '1.80']] [['nom', 'age', 'taille'], ['Alice', '30', '1.65'], ["Bob L'éponge", '25', '1.75'], ['Charlie', '28', '1.80']] Données sauvegardées dans donnees.txt ! [['nom', 'age', 'taille'], ['Alice', '30', '1.65'], ["Bob L'éponge", '25', '1.75'], ['Charlie', '28', '1.80']]
import os
def listing():
# Spécifiez le chemin du répertoire que vous souhaitez lister.
# Par exemple, pour le répertoire courant, utilisez '.'.
chemin_repertoire = '.'
# Obtenir la liste des fichiers
fichiers = os.listdir(chemin_repertoire)
# Afficher la liste des fichiers
for fichier in fichiers:
print(fichier)
def effacer(file):
# Spécifiez le chemin du fichier que vous souhaitez effacer avec son nom et extension
chemin_fichier = file
# Vérifiez si le fichier existe avant de le supprimer
if os.path.exists(chemin_fichier):
os.remove(chemin_fichier)
print(f"Le fichier {chemin_fichier} a été effacé.")
else:
print(f"Le fichier {chemin_fichier} n'existe pas.")
listing()
effacer('donnees.txt')donnees.txt Le fichier donnees.txt a été effacé.
Problème d'encodage
Si vous rencontrez des problèmes de caractères lors de la lecture d'un fichier, il est probable que vous soyez confronté à des questions d'encodage. L'encodage le plus couramment utilisé aujourd'hui est UTF-8, mais il existe de nombreux autres encodages, tels que ISO-8859-1, Windows-1252, etc.
Spécifier l'encodage lors de l'ouverture du fichier :
En Python, vous pouvez spécifier l'encodage lors de l'ouverture d'un fichier avec l'argument encoding. Par exemple, pour ouvrir un fichier en UTF-8 :
with open(file, 'r', encoding='utf-8') as fichier:
contenu = fichier.read()
print(contenu)Donnees et csv
Voici un exemple de programmes Python qui prend en entrée des données, les sauvegarde dans un fichier csv, puis les modifie.
Maintenant le csv peut être créé directement par un logiciel comme Excel.
import csv
def sauvegarde_csv(file, donnees):
with open(file, mode='w', newline='') as fichier:
# Vérifier si 'donnees' contient des dictionnaires ou des listes
if isinstance(donnees[0], dict):
# Si les données sont des dictionnaires, extraire les en-têtes des clés du premier élément
fieldnames = donnees[0].keys()
writer_csv = csv.DictWriter(fichier, fieldnames=fieldnames)
writer_csv.writeheader()
writer_csv.writerows(donnees)
else:
# Si les données sont des listes, le premier élément contient les en-têtes
writer_csv = csv.writer(fichier)
writer_csv.writerows(donnees)
print(f"Données sauvegardées dans {file} !")
def import_csv(file):
donnees = []
with open(file, 'r') as fichier:
lecteur = csv.DictReader(fichier)
for ligne in lecteur:
donnees.append(dict(ligne))
return donnees
donnees = [
['nom', 'age', 'taille'],
['Alice', '30', '1.65'],
['Bob', '25', '1.75'],
['Charlie', '28', '1.80']
]
sauvegarde_csv('donnees.csv',donnees)
print()
donnees= import_csv('donnees.csv')
print(donnees)Données sauvegardées dans donnees.csv !
[{'nom': 'Alice', 'age': '30', 'taille': '1.65'}, {'nom': 'Bob', 'age': '25', 'taille': '1.75'}, {'nom': 'Charlie', 'age': '28', 'taille': '1.80'}]
print(donnees)
donnees[1]['nom'] = "Bob L'éponge"
print(donnees)
sauvegarde_csv('donnees.csv',donnees)[{'nom': 'Alice', 'age': '30', 'taille': '1.65'}, {'nom': 'Bob', 'age': '25', 'taille': '1.75'}, {'nom': 'Charlie', 'age': '28', 'taille': '1.80'}]
[{'nom': 'Alice', 'age': '30', 'taille': '1.65'}, {'nom': "Bob L'éponge", 'age': '25', 'taille': '1.75'}, {'nom': 'Charlie', 'age': '28', 'taille': '1.80'}]
Données sauvegardées dans donnees.csv !
listing()
effacer('donnees.csv')donnees.csv Le fichier donnees.csv a été effacé.
Tableau de p-uplets qui partagent les mêmes descripteurs
Le tableau de données est un peu différents. Mais sinon le reste est identique
donnees = [
('nom', 'age', 'taille'),
('Alice', '30', '1.65'),
('Bob', '25', '1.75'),
('Charlie', '28', '1.80')
]sauvegarde_csv('donnees.csv',donnees)
print()
print(import_csv('donnees.csv'))Données sauvegardées dans donnees.csv !
[{'nom': 'Alice', 'age': '30', 'taille': '1.65'}, {'nom': 'Bob', 'age': '25', 'taille': '1.75'}, {'nom': 'Charlie', 'age': '28', 'taille': '1.80'}]
sauvegarde_texte('donnees.txt', donnees)
print()
print(import_texte('donnees.txt'))Données sauvegardées dans donnees.txt ! [['nom', 'age', 'taille'], ['Alice', '30', '1.65'], ['Bob', '25', '1.75'], ['Charlie', '28', '1.80']]
listing()
effacer('donnees.csv')
effacer('donnees.txt')donnees.csv donnees.txt Le fichier donnees.csv a été effacé. Le fichier donnees.txt a été effacé.
Remarque Perso :
Un tableau doublement indexé ou un tableau de p-uplets qui partagent les mêmes descripteurs s'est bien, mais utiliser des dataframes ou du SQL s'est mieux !
3.2 - CSV Recherche ✔
Traitement de données en tables
Recherche dans une table
Capacités attendus :
Rechercher les lignes d’une table vérifiant des critères exprimés en logique propositionnelle.
Commentaires :
La recherche de doublons, les tests de cohérence d’une table sont présentés.
etudiants = [
{"nom": "Alice", "age": 22, "matière": "Informatique"},
{"nom": "Bob", "age": 19, "matière": "Mathématiques"},
{"nom": "Charlie", "age": 23, "matière": "Informatique"},
{"nom": "Diana", "age": 20, "matière": "Biologie"},
{"nom": "Eva", "age": 21, "matière": "Chimie"},
{"nom": "Frank", "age": 24, "matière": "Mathématiques"},
{"nom": "Grace", "age": 18, "matière": "Littérature"},
{"nom": "Hugo", "age": 22, "matière": "Philosophie"},
{"nom": "Iris", "age": 19, "matière": "Arts"},
{"nom": "Jack", "age": 21, "matière": "Mathématiques"},
{"nom": "Kathy", "age": 21, "matière": "Chimie"},
{"nom": "Liam", "age": 2, "matière": "Géographie"},
{"nom": "Mona", "age": 23, "matière": "Musique"},
{"nom": "Eva", "age": 18, "matière": "Droit"},
{"nom": "Olivia", "age": 20, "matière": "Médecine"},
# ... et ainsi de suite
]Rechercher les lignes d’une table vérifiant des critères exprimés en logique propositionnelle
Pour trouver tous les étudiants majeurs en "Informatique" âgés de plus de 20 ans :
resultats = [e for e in etudiants if e["matière"] == "Mathématiques" and e["age"] > 20]
print(resultats)[{'nom': 'Frank', 'age': 24, 'matière': 'Mathématiques'}, {'nom': 'Jack', 'age': 21, 'matière': 'Mathématiques'}]
Recherche de doublons
noms_vus = []
doublons = []
for e in etudiants:
if e["nom"] in noms_vus:
if e["nom"] not in doublons:
doublons.append(e["nom"])
else:
noms_vus.append(e["nom"])
print("Doublons trouvés:", doublons)Doublons trouvés: ['Eva']
Tests de cohérence d’un tableau
Il est essentiel de s'assurer que les données du tableau sont cohérentes.
incoherences = [e for e in etudiants if e["age"] < 5]
if incoherences:
print("Incohérences trouvées:", incoherences)
else:
print("Toutes les données sont cohérentes.")Incohérences trouvées: [{'nom': 'Liam', 'age': 2, 'matière': 'Géographie'}]
3.3 - CSV Tri ✔
Traitement de données en tables
Tri d’une table
Capacités attendus :
Trier une table suivant une colonne.
Commentaires :
Une fonction de tri intégrée au système ou à une bibliothèque peut être utilisée.
etudiants = [
{"nom": "Alice", "age": 22, "matière": "Informatique", "note": 85, "ville": "Paris"},
{"nom": "Bob", "age": 19, "matière": "Mathématiques", "note": 90, "ville": "Lyon"},
{"nom": "Charlie", "age": 24, "matière": "Informatique", "note": 78, "ville": "Lille"},
{"nom": "Diana", "age": 21, "matière": "Biologie", "note": 92, "ville": "Toulouse"},
{"nom": "Eva", "age": 20, "matière": "Chimie", "note": 88, "ville": "Nice"},
{"nom": "Frank", "age": 27, "matière": "Physique", "note": 80, "ville": "Strasbourg"},
{"nom": "Grace", "age": 18, "matière": "Mathématiques", "note": 89, "ville": "Nantes"},
{"nom": "Hugo", "age": 23, "matière": "Histoire", "note": 95, "ville": "Bordeaux"},
{"nom": "Iris", "age": 25, "matière": "Informatique", "note": 70, "ville": "Lille"},
{"nom": "Jack", "age": 22, "matière": "Littérature", "note": 82, "ville": "Rennes"},
{"nom": "Kathy", "age": 20, "matière": "Philosophie", "note": 87, "ville": "Reims"},
{"nom": "Liam", "age": 19, "matière": "Informatique", "note": 93, "ville": "Clermont-Ferrand"},
{"nom": "Mona", "age": 23, "matière": "Mathématiques", "note": 75, "ville": "Montpellier"},
{"nom": "Nate", "age": 21, "matière": "Biologie", "note": 91, "ville": "Grenoble"},
{"nom": "Olivia", "age": 24, "matière": "Chimie", "note": 85, "ville": "Dijon"},
{"nom": "Paul", "age": 26, "matière": "Physique", "note": 78, "ville": "Angers"},
{"nom": "Quinn", "age": 22, "matière": "Histoire", "note": 80, "ville": "Brest"},
{"nom": "Rita", "age": 20, "matière": "Littérature", "note": 88, "ville": "Le Mans"},
{"nom": "Sam", "age": 19, "matière": "Philosophie", "note": 87, "ville": "Amiens"},
{"nom": "Tina", "age": 23, "matière": "Informatique", "note": 90, "ville": "Tours"},
# ... et ainsi de suite
]def afficher_tableau(etudiants):
# Afficher les en-têtes de colonne
print("{:<10} | {:<5} | {:<15} | {:<5} | {:<15}".format("Nom", "Âge", "Matière", "Note", "Ville"))
print("-"*60) # Une ligne séparatrice pour la clarté
# Parcourir chaque étudiant et afficher leurs informations formatées
for etudiant in etudiants:
print("{:<10} | {:<5} | {:<15} | {:<5} | {:<15}".format(
etudiant["nom"], etudiant["age"], etudiant["matière"], etudiant["note"], etudiant["ville"]
))
# Appel de la fonction avec le tableau 'etudiants'
afficher_tableau(etudiants)Nom | Âge | Matière | Note | Ville ------------------------------------------------------------ Alice | 22 | Informatique | 85 | Paris Bob | 19 | Mathématiques | 90 | Lyon Charlie | 24 | Informatique | 78 | Marseille Diana | 21 | Biologie | 92 | Toulouse Eva | 20 | Chimie | 88 | Nice Frank | 27 | Physique | 80 | Strasbourg Grace | 18 | Mathématiques | 89 | Nantes Hugo | 23 | Histoire | 95 | Bordeaux Iris | 25 | Informatique | 70 | Lille Jack | 22 | Littérature | 82 | Rennes Kathy | 20 | Philosophie | 87 | Reims Liam | 19 | Informatique | 93 | Clermont-Ferrand Mona | 23 | Mathématiques | 75 | Montpellier Nate | 21 | Biologie | 91 | Grenoble Olivia | 24 | Chimie | 85 | Dijon Paul | 26 | Physique | 78 | Angers Quinn | 22 | Histoire | 80 | Brest Rita | 20 | Littérature | 88 | Le Mans Sam | 19 | Philosophie | 87 | Amiens Tina | 23 | Informatique | 90 | Tours
Tri Croissant par Âge
etudiants_tries_par_age = sorted(etudiants, key=lambda x: x["age"])
afficher_tableau(etudiants_tries_par_age)Nom | Âge | Matière | Note | Ville ------------------------------------------------------------ Grace | 18 | Mathématiques | 89 | Nantes Bob | 19 | Mathématiques | 90 | Lyon Liam | 19 | Informatique | 93 | Clermont-Ferrand Sam | 19 | Philosophie | 87 | Amiens Eva | 20 | Chimie | 88 | Nice Kathy | 20 | Philosophie | 87 | Reims Rita | 20 | Littérature | 88 | Le Mans Diana | 21 | Biologie | 92 | Toulouse Nate | 21 | Biologie | 91 | Grenoble Alice | 22 | Informatique | 85 | Paris Jack | 22 | Littérature | 82 | Rennes Quinn | 22 | Histoire | 80 | Brest Hugo | 23 | Histoire | 95 | Bordeaux Mona | 23 | Mathématiques | 75 | Montpellier Tina | 23 | Informatique | 90 | Tours Charlie | 24 | Informatique | 78 | Marseille Olivia | 24 | Chimie | 85 | Dijon Iris | 25 | Informatique | 70 | Lille Paul | 26 | Physique | 78 | Angers Frank | 27 | Physique | 80 | Strasbourg
Tri Décroissant par Note
etudiants_tries_par_note_desc = sorted(etudiants, key=lambda x: x["note"], reverse=True)
afficher_tableau(etudiants_tries_par_note_desc)Nom | Âge | Matière | Note | Ville ------------------------------------------------------------ Hugo | 23 | Histoire | 95 | Bordeaux Liam | 19 | Informatique | 93 | Clermont-Ferrand Diana | 21 | Biologie | 92 | Toulouse Nate | 21 | Biologie | 91 | Grenoble Bob | 19 | Mathématiques | 90 | Lyon Tina | 23 | Informatique | 90 | Tours Grace | 18 | Mathématiques | 89 | Nantes Eva | 20 | Chimie | 88 | Nice Rita | 20 | Littérature | 88 | Le Mans Kathy | 20 | Philosophie | 87 | Reims Sam | 19 | Philosophie | 87 | Amiens Alice | 22 | Informatique | 85 | Paris Olivia | 24 | Chimie | 85 | Dijon Jack | 22 | Littérature | 82 | Rennes Frank | 27 | Physique | 80 | Strasbourg Quinn | 22 | Histoire | 80 | Brest Charlie | 24 | Informatique | 78 | Marseille Paul | 26 | Physique | 78 | Angers Mona | 23 | Mathématiques | 75 | Montpellier Iris | 25 | Informatique | 70 | Lille
Tri avec conditions
# Filtrage des étudiants qui étudient l'Informatique et âge croissant
etudiants_informatique = [e for e in etudiants if e["matière"] == "Informatique" and e["ville"] == "Lille"]
etudiants_tries = sorted(etudiants_informatique, key=lambda x: x["age"])
afficher_tableau(etudiants_tries)Nom | Âge | Matière | Note | Ville ------------------------------------------------------------ Charlie | 24 | Informatique | 78 | Lille Iris | 25 | Informatique | 70 | Lille
3.4 - CSV Fusion ✔
Traitement de données en tables
Fusion de tables
Capacités attendus :
Construire une nouvelle table en combinant les données de deux tables.
(Moi, j'ai fait pour trois tables!)
Commentaires :
La notion de domaine de valeurs est mise en évidence
etudiants = [
{"id_etudiant": 1, "nom": "Alice", "age": 22, "ville": "Paris"},
{"id_etudiant": 2, "nom": "Bob", "age": 19, "ville": "Lyon"},
{"id_etudiant": 3, "nom": "Charlie", "age": 24, "ville": "Marseille"},
{"id_etudiant": 4, "nom": "Diana", "age": 21, "ville": "Toulouse"},
{"id_etudiant": 5, "nom": "Eva", "age": 20, "ville": "Nice"},
{"id_etudiant": 6, "nom": "Frank", "age": 27, "ville": "Strasbourg"},
{"id_etudiant": 7, "nom": "Grace", "age": 18, "ville": "Nantes"},
{"id_etudiant": 8, "nom": "Hugo", "age": 23, "ville": "Bordeaux"},
{"id_etudiant": 9, "nom": "Iris", "age": 25, "ville": "Lille"},
{"id_etudiant": 10, "nom": "Jack", "age": 22, "ville": "Rennes"},
]
matieres = [
{"id_matiere": 1, "nom_matiere": "Informatique"},
{"id_matiere": 2, "nom_matiere": "Mathématiques"},
{"id_matiere": 3, "nom_matiere": "Histoire"},
{"id_matiere": 4, "nom_matiere": "Chimie"},
{"id_matiere": 5, "nom_matiere": "Physique"},
{"id_matiere": 6, "nom_matiere": "Littérature"},
{"id_matiere": 7, "nom_matiere": "Philosophie"},
{"id_matiere": 8, "nom_matiere": "Biologie"},
]
notes = [
{"id_etudiant": 1, "id_matiere": 1, "note": 85},
{"id_etudiant": 2, "id_matiere": 2, "note": 90},
{"id_etudiant": 1, "id_matiere": 3, "note": 78},
{"id_etudiant": 3, "id_matiere": 4, "note": 88},
{"id_etudiant": 4, "id_matiere": 5, "note": 92},
{"id_etudiant": 5, "id_matiere": 1, "note": 80},
{"id_etudiant": 6, "id_matiere": 6, "note": 85},
{"id_etudiant": 7, "id_matiere": 7, "note": 90},
{"id_etudiant": 8, "id_matiere": 8, "note": 87},
{"id_etudiant": 9, "id_matiere": 2, "note": 79},
{"id_etudiant": 10, "id_matiere": 3, "note": 88},
]
def afficher_table(nom_table, table):
print(f"\n---- Table {nom_table} ----")
# Récupération des en-têtes à partir des clés du premier élément
en_tetes = list(table[0].keys())
# Calcul de la largeur de chaque colonne en fonction du contenu le plus long et des en-têtes
largeurs = [max(len(str(item[colonne])) if item else 0 for item in table) for colonne in en_tetes]
largeurs = [max(largeurs[i], len(en_tetes[i])) for i in range(len(largeurs))]
# Formatage des en-têtes avec la largeur calculée
ligne_en_tete = " | ".join([en_tetes[i].ljust(largeurs[i]) for i in range(len(en_tetes))])
print(ligne_en_tete)
print("-" * len(ligne_en_tete)) # Ligne séparatrice
# Affichage de chaque ligne de la table
for item in table:
ligne = " | ".join([str(item[colonne]).ljust(largeurs[i]) for i, colonne in enumerate(en_tetes)])
print(ligne)
# Utilisation de la fonction pour afficher les tables
afficher_table("Étudiants", etudiants)
afficher_table("Matières", matieres)
afficher_table("Notes", notes)
---- Table Étudiants ---- id_etudiant | nom | age | ville ---------------------------------------- 1 | Alice | 22 | Paris 2 | Bob | 19 | Lyon 3 | Charlie | 24 | Marseille 4 | Diana | 21 | Toulouse 5 | Eva | 20 | Nice 6 | Frank | 27 | Strasbourg 7 | Grace | 18 | Nantes 8 | Hugo | 23 | Bordeaux 9 | Iris | 25 | Lille 10 | Jack | 22 | Rennes ---- Table Matières ---- id_matiere | nom_matiere -------------------------- 1 | Informatique 2 | Mathématiques 3 | Histoire 4 | Chimie 5 | Physique 6 | Littérature 7 | Philosophie 8 | Biologie ---- Table Notes ---- id_etudiant | id_matiere | note ------------------------------- 1 | 1 | 85 2 | 2 | 90 1 | 3 | 78 3 | 4 | 88 4 | 5 | 92 5 | 1 | 80 6 | 6 | 85 7 | 7 | 90 8 | 8 | 87 9 | 2 | 79 10 | 3 | 88
table_fusionnee = []
for note in notes:
etudiant_correspondant = None
for e in etudiants:
if e["id_etudiant"] == note["id_etudiant"]:
etudiant_correspondant = e
break
matiere_correspondante = None
for m in matieres:
if m["id_matiere"] == note["id_matiere"]:
matiere_correspondante = m
break
if etudiant_correspondant and matiere_correspondante: # S'assure que les deux correspondances ont été trouvées
fusion = {
"nom_etudiant": etudiant_correspondant["nom"],
"age": etudiant_correspondant["age"],
"ville": etudiant_correspondant["ville"],
"matiere": matiere_correspondante["nom_matiere"],
"note": note["note"]
}
table_fusionnee.append(fusion)
afficher_table("Fusion", table_fusionnee)---- Table Fusion ---- nom_etudiant | age | ville | matiere | note ------------------------------------------------------ Alice | 22 | Paris | Informatique | 85 Bob | 19 | Lyon | Mathématiques | 90 Alice | 22 | Paris | Histoire | 78 Charlie | 24 | Marseille | Chimie | 88 Diana | 21 | Toulouse | Physique | 92 Eva | 20 | Nice | Informatique | 80 Frank | 27 | Strasbourg | Littérature | 85 Grace | 18 | Nantes | Philosophie | 90 Hugo | 23 | Bordeaux | Biologie | 87 Iris | 25 | Lille | Mathématiques | 79 Jack | 22 | Rennes | Histoire | 88
Domaine de valeur
La notion de domaine de valeurs fait généralement référence à l'ensemble spécifique de valeurs qu'une certaine colonne ou attribut peut prendre. C'est différent du type de données.
Le type, c'est la nature de la valeur. Par exemple, entier, chaîne de caractères, flottant, booléen, etc.
def afficher_types_et_domaines(table, nom_table):
print(f"\n---- {nom_table} ----")
for colonne in table[0]: # Utiliser le premier élément comme référence pour les colonnes
valeurs = [ligne[colonne] for ligne in table]
types = {type(valeur).__name__ for valeur in valeurs}
domaines = set(valeurs)
print(f"Colonne: {colonne}")
print(f"Types de données: {types}")
print(f"Domaine de valeurs: {domaines}")
print()
afficher_types_et_domaines(etudiants, "Étudiants")
afficher_types_et_domaines(matieres, "Matières")
afficher_types_et_domaines(notes, "Notes")
---- Étudiants ----
Colonne: id_etudiant
Types de données: {'int'}
Domaine de valeurs: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Colonne: nom
Types de données: {'str'}
Domaine de valeurs: {'Bob', 'Frank', 'Charlie', 'Grace', 'Jack', 'Hugo', 'Diana', 'Eva', 'Alice', 'Iris'}
Colonne: age
Types de données: {'int'}
Domaine de valeurs: {18, 19, 20, 21, 22, 23, 24, 25, 27}
Colonne: ville
Types de données: {'str'}
Domaine de valeurs: {'Nantes', 'Nice', 'Bordeaux', 'Marseille', 'Toulouse', 'Strasbourg', 'Rennes', 'Lyon', 'Paris', 'Lille'}
---- Matières ----
Colonne: id_matiere
Types de données: {'int'}
Domaine de valeurs: {1, 2, 3, 4, 5, 6, 7, 8}
Colonne: nom_matiere
Types de données: {'str'}
Domaine de valeurs: {'Biologie', 'Physique', 'Mathématiques', 'Informatique', 'Histoire', 'Philosophie', 'Littérature', 'Chimie'}
---- Notes ----
Colonne: id_etudiant
Types de données: {'int'}
Domaine de valeurs: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Colonne: id_matiere
Types de données: {'int'}
Domaine de valeurs: {1, 2, 3, 4, 5, 6, 7, 8}
Colonne: note
Types de données: {'int'}
Domaine de valeurs: {78, 79, 80, 85, 87, 88, 90, 92}
4.1 - IHM ✔
Interactions entre l’homme et la machine sur le Web
Modalités de l’interaction entre l’homme et la machine
Événements
Interaction avec l’utilisateur dans une page Web
Capacités attendues :
- Identifier les différents composants graphiques permettant d’interagir avec une application Web.
- Identifier les événements que les fonctions associées aux différents composants graphiques sont capables de traiter.
- Interaction avec l’utilisateur dans une page Web.
Commentaires :
- Il s’agit d’examiner le code HTML d’une page comprenant des composants graphiques et de distinguer ce qui relève de la description des composants graphiques en HTML de leur comportement (réaction aux événements) programmé par exemple en JavaScrip.
- Analyser et modifier les méthodes exécutées lors d’un clic sur un bouton d’une page WEB.
1. Le cas le plus simple : la même page pour tout le monde
Nous allons tout d'abord considérer le cas où le serveur renvoie une page unique, identique pour tous les utilisateurs. De plus, l'utilisateur ne pourra pas agir sur sa page : il n'y a aucune interactivité.
Exemple de page statique côté serveur et côté utilisateur :
- cette merveille de page web cette merveille de page web.
- plus complète, mais tout aussi statique : cette page Wikipedia consacrée à John Conway.
1.1 html
Lorsque le client demande au serveur le contenu d'une page web, celui-ci lui renvoie, dans le cas le plus simple, une simple page html.
html est un langage dit à balises ». Ce n'est pas à proprement parler un langage de programmation, mais plutôt un langage de description de contenu. Il a été inventé en 1992 par `Tim Berners-Lee``. La version actuellement utilisée est le html5.
<!DOCTYPE html>
<body>
<p>Ceci est le texte introductif de ma page.</p>
<p>
<h1> Ceci est un titre de niveau 1 </h1>
Mais sans rien d'intéressant.
<h2> Ceci est un titre de niveau 2 </h2>
<ul>
<li> le début d'une liste indentée </li>
<li> la suite ... </li>
</ul>
<a href="https://developer.mozilla.org/fr/docs/Apprendre/HTML/Getting_started.htm">Exemple ici</a>
</p>
</body>Vous pouvez contempler cette page : ici.
Exercice 1
a) Créez un dossier contenant un fichier mapage.html.
b) Créez une page contenant une image et un lien vers le site du lycée.
1.2 html + css
L'acronyme css signifie Cascading Style Sheets. L'idée est de regrouper dans un seul fichier toutes les informations relatives à la mise en forme des éléments de la page html.
Se manière très simplifiée, on peut dire que le fichier html s'occupe du fond tandis que le fichier css s'occupe de la forme.
Le fichier css, souvent nommé style.css, et appelé feuille de style doit être référencé au début du fichier html , au sein de la balise
.- fichier index.html :
<!DOCTYPE html>
Ceci est un titre de niveau 1
Mais sans rien d'intéressant.Ceci est un titre de niveau 2
- fichier style.css :
html { font-size: 15px; font-family: sans-serif; background-color: lightgray; }
h1 { color: red; }
Vous pouvez contempler cette page : ici.
Exercice 2
Reprenez votre page de l'exercice 1 et rajoutez une feuille de style.
Exercice 3
Allez sur le site http://sudouest.fr, affichez l'inspecteur d'élement de votre navigateur, puis modifiez le plus possible les attributs de style de la page.-
2 ) Quand le client peut agir sur sa page : exemple avec JavaScript
Jusqu'à présent, la page web envoyée par le serveur est :
- identique quel que soit le client.
- statique après réception sur l'ordinateur du client.
Le JavaScript va venir régler le problème n°2 : il est possible de fabriquer une page sur laquelle le client va pouvoir agir localement, sans avoir à redemander une nouvelle page au serveur.
Inventé en 1995 par Brendan Eich pour le navigateur Netscape, le langage JavaScript s'est imposé comme la norme auprès de tous les navigateurs pour apporter de l'interactivité aux pages web.
Notre fichier index.html fait référence, au sein d'une balise script, à un fichier externe script.js qui contiendra notre code JavaScript.
- fichier index.html :
<!DOCTYPE html>
Une page web extrêmement dynamique
<label>Changez la couleur d'arrière-plan:</label>
<button type="button" onclick="choix('yellow');">jaune</button>
<button type="button" onclick="choix('green');">vert</button>
<button type="button" onclick="choix('purple');">violet</button>
</div>
<div>
<p>
En JavaScript, le nom de la couleur choisie est :
</p>
<p id="resultat"></p>
</div>- fichier script.js :
function choix(color){
document.body.style.background = color;
document.getElementById("resultat").innerHTML=color;
}Vous pouvez contempler cette page : ici.
Commentaires
- Au sein du bouton déclaré par la balise button, l'attribut onclick reçoit le nom d'une fonction déclarée à l'intérieur du fichier script.js, ici la fonction choix().
- Cette fonction nous permet de modifier à la fois l'aspect esthétique de la page (changement de la couleur de background) mais aussi le contenu de cette page, en faisant afficher le nom de la couleur.
La puissance du JavaScript permet de réaliser aujourd'hui des interfaces utilisateurs très complexes au sein d'un navigateur, équivalentes à celles produites par des logiciels externes (pensez à Discord, par ex.). Bien sûr, dans ces cas complexes, le serveur est aussi sollicité pour modifier la page, comme nous le verrons en partie 3.
En savoir plus
- le guide JavaScript de la fondation Mozilla : https://developer.mozilla.org/fr/docs/Web/JavaScript/Guide
- le cours d'OpenClassrooms : https://openclassrooms.com/fr/courses/2984401-apprenez-a-coder-avec-javascript
3. Quand la page est fabriquée à la demande pour le client : exemple avec PHP
Rappelons que toutes les pages que nous avons créées jusqu'à présent sont uniformément envoyées par le serveur au client. Aucune «préparation» de la page en amont n'a lieu sur le serveur, aucun dialogue n'a lieu avec le serveur une fois que la page a été livrée. Évidemment, si le web était comme ceci, il ne serait qu'une gigantesque bibliothèque en consultation seule (ce fut le cas pendant longtemps).
Les langages serveurs : PHP,Python, Java, Ruby, C#, permettent de rajouter de l'interactivité côté serveur.
Il convient de rappeler la différence fondamentale entre :
-
une page statique (côté serveur) :
Lors d'une requête d'un client vers un serveur, si le client demande la page index.html, une copie exacte du fichier index.html est transmise au client sur sa machine. Depuis votre navigateur, l'affichage du code-source (par Ctrl-U) vous donnera le fichier html tel qu'il était stocké sur le serveur. -
et une page dynamique (côté serveur) :
Lors d'une requête d'un client vers un serveur, si le client demande la page test.php, un code html est généré à partir du fichier test.php puis est transmise au client sur sa machine. Le fichier transmis ne contient plus de balises php, il ne comporte que des balises html classiques. Exemple : https://webftts.com/index.php
date.php :
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8" />
<title>Quel jour sommes-nous</title>
</head>
<body>
<p>
<?php
$date = date("d-m-Y");
Print("Nous sommes le $date");
?>
</p>
</body>
</html>On y repère la balise ?php ....?> Ce code php a donc généré, lors de l'appel au serveur, le code html :
Nous somme le 13-04-2023
Vous pouvez tester cette page : ici.
Voilà comment un serveur peut adapter la page qu'il renvoie, suivant l'utilisateur qui la demande. Nous verrons prochainement comment par des requêtes le client peut envoyer des paramètres au serveur, et comment celui-ci modifie sa réponse en conséquence.
4.2 - Requêtes HTTP ✔
Interactions entre l’homme et la machine sur le Web
Interaction client-serveur, Requêtes HTTP, Réponses du serveur
Capacités attendues :
- Distinguer ce qui est exécuté sur le client ou sur le serveur et dans quel ordre.
- Distinguer ce qui est mémorisé dans le client et retransmis au serveur.
- Reconnaître quand et pourquoi la transmission est chiffrée.
Commentaires :
Il s’agit de faire le lien avec ce qui a été vu en classe de seconde et d’expliquer comment on peut passer des paramètres à un site grâce au protocole HTTP
Le protocole HTTP : des requêtes et des réponses
HTTP (HyperText Transfer Protocol) est le protocole qui régit la communication entre :
- le client (la machine de l'utilisateur qui souhaite obtenir une page web). On dit que le client effectue une requête.
- le serveur (la machine sur laquelle sont stockés les fichiers nécessaires à l'affichage de cette page web). Le serveur va renvoyer une réponse.
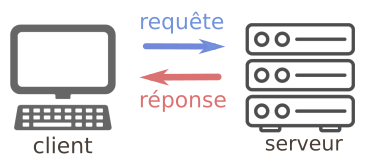
Déroulé d'une requête
Prenons pour exemple la requête d'un navigateur vers la page https://webftts.com/
- le navigateur analyse l'url : la demande concerne la page interesting.html, stockée sur le serveur webftts.com.
- une demande est préalablement effectuée auprès pour obtenir l'adresse IP du serveur glassus1.free.fr (qui est en fait un sous-domaine du serveur des pages personnelles de l'opérateur Free). Ici, l'adresse IP sera 212.27.63.111 (on la retrouvera dans la capture de la fenêtre d'Outils de devéloppement).
- la requête est effectuée sur le port 80 de l'adresse 212.27.63.111.
- la réponse est envoyée au navigateur, qui en extrait la charge utile et procède à l'affichage de la page.
Analyse à l'aide d'un navigateur
Observons à partir de l'Inspecteur d'élément d'un navigateur (ici Firefox) les informations qui transitent lors de la requête et de la réponse.
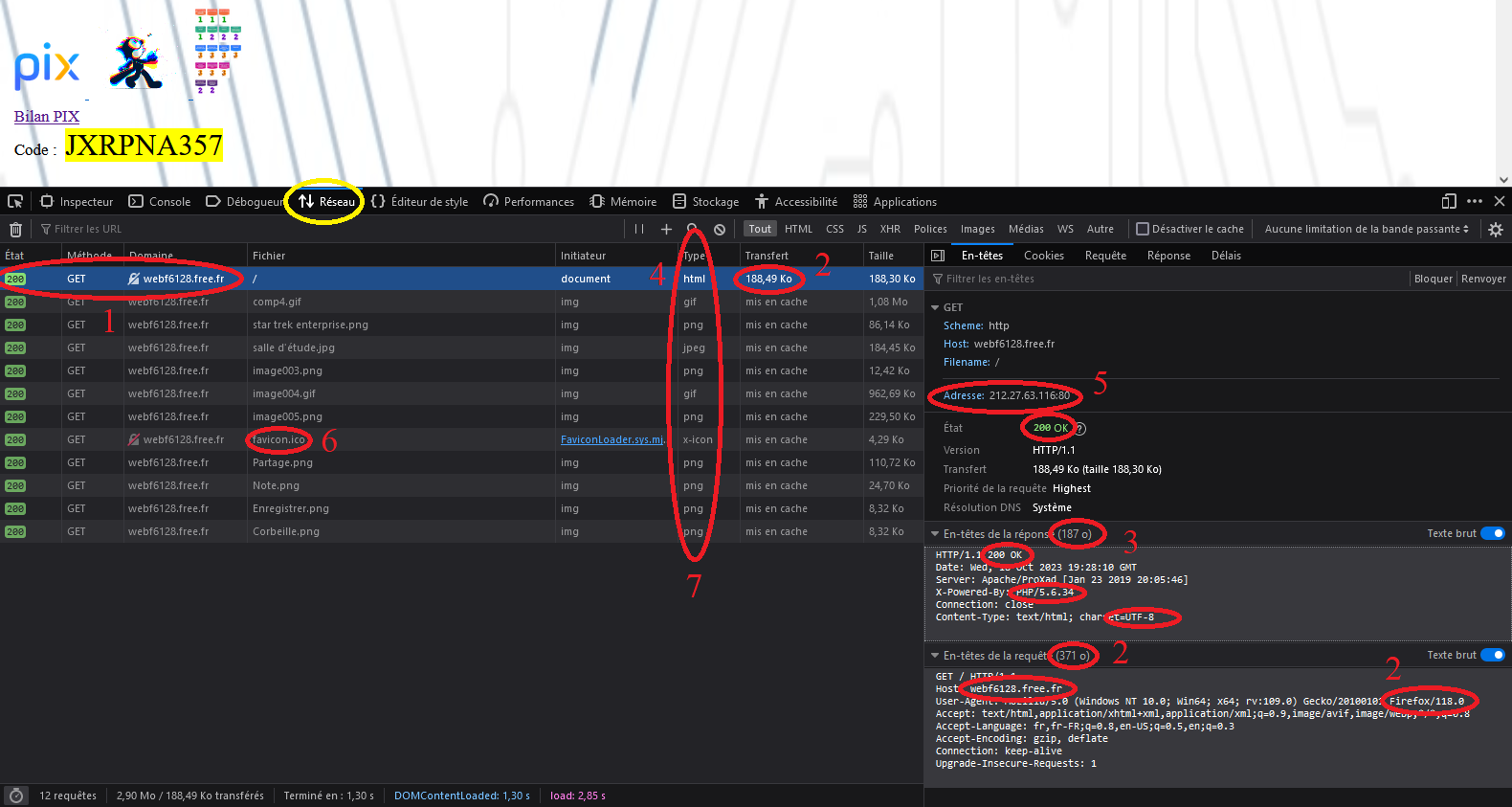
On se place sur l'onglet réseau, puis on va sur la page https://webftts.com/
- Point 1 : La requête de type GET vers l'url https://webftts.com/ non sécurisée, a généré un code de réponse 200 OK, ce qui signifie que la requête a été traitée et que la réponse contenant la page a été envoyée.
Vous pouvez trouver à l'adresse https://developer.mozilla.org/fr/docs/Web/HTTP/Status la totalité des codes de réponse possibles.
Citons par exemple :
- 304 Not Modified : la page n'a pas eu besoin d'être renvoyée
- 403 Forbidden : le client n'a pas le droit d'accès à la page.
- 404 Not Found : la page demandée est introuvable
- 500 Internal Server Error : le serveur a rencontré une erreur qu'il ne sait pas traiter.
- Point 2 et 3 : en observant la taille totale des données transférées (188,49 ko), on peut comprendre que la réponse faite par le serveur est constituée :
- d'un En-tête de requête de mon ordinateur de 371 octets avec Firefox vers 118,
- du corps de la Réponse de 187, indiquant la version php 5.6.34 du site webftts.com
- Point 4 : Elle contient le code html de la page.
- Point 5 : que l'ip du site est 212.27.63.116 sur le port 30
- Point 6 : On peut observer que le navigateur a aussi effectué (de sa propre initiative) une requête vers un fichier favicon.ico qui est l'icone de la page web dans les onglets du navigateur ou la barre de favoris. Ce fichier était bien présent sur le serveur (ce n'est pas toujours le cas), il a donc été envoyé dans la réponse du serveur.
- Point 7 : Et aussi l'appel au site webftts.com génère des requête/réponses différentes, composées de fichiers html,png, gif, jpeg,...
4.3 - GET POST ✔
Interactions entre l’homme et la machine sur le Web
Formulaire d’une page Web
Capacités attendues :
- Analyser le fonctionnement d’un formulaire simple.
- Distinguer les transmissions de paramètres par les requêtes POST ou GET.
Commentaires :
Discuter les deux types de requêtes selon le type des valeurs à transmettre et/ou leur confidentialifé.
1. Exemple de formulaire
Pour tester le formuler, cliquez sur le lien suivant : Formulaire de contact
# Formulaire contact.html
<!DOCTYPE html>
<html lang="fr">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>Formulaire de Contact</title>
</head>
<body>
<h1>Formulaire de Contact</h1>
<form action="Formulaire_contact_traitement.php" method="POST">
<label for="nom">Nom :</label><br>
<input type="text" id="nom" name="nom" required><br><br>
<label for="email">Email :</label><br>
<input type="email" id="email" name="email" required><br><br>
<label for="message">Message :</label><br>
<textarea id="message" name="message" rows="4" cols="50" required></textarea><br><br>
<label>Options :</label><br>
<input type="checkbox" id="newsletter" name="newsletter">
<label for="newsletter">S'abonner à la newsletter</label><br><br>
<input type="checkbox" id="conditions" name="conditions" required>
<label for="conditions">J'accepte les conditions d'utilisation</label><br><br>
<input type="submit" value="Envoyer">
</form>
</body>
</html># Formulaire_contact_traitement.php
<?php
if ($_SERVER["REQUEST_METHOD"] == "POST") {
// Récupérer les données du formulaire
$nom = isset($_POST['nom']) ? htmlspecialchars($_POST['nom']) : '';
$email = isset($_POST['email']) ? htmlspecialchars($_POST['email']) : '';
$message = isset($_POST['message']) ? htmlspecialchars($_POST['message']) : '';
// Récupérer les cases à cocher
$newsletter = isset($_POST['newsletter']) ? 'Oui' : 'Non';
$conditions = isset($_POST['conditions']) ? 'Oui' : 'Non';
// Affichage des données récupérées
echo "<h1>Récapitulatif de votre message :</h1>";
echo "<p><strong>Nom :</strong> " . $nom . "</p>";
echo "<p><strong>Email :</strong> " . $email . "</p>";
echo "<p><strong>Message :</strong> " . nl2br($message) . "</p>";
echo "<p><strong>S'abonner à la newsletter :</strong> " . $newsletter . "</p>";
echo "<p><strong>Accepte les conditions d'utilisation :</strong> " . $conditions . "</p>";
}
?>2. La méthode GET et la méthode POST
2.1. La méthode GET
Nous avons la page html suivante :
Vous pouvez tester ce script à l'adresse : https://webftts.com/mdp/mdp_get.html
Il s'agit de ce que l'on appelle un formulaire qui sera envoyé vers le script cible.php présent sur le serveur, après avoir appuyé sur le bouton Valider.
Le paramètre de pass est de type password, ce qui signifie qu'on n'affichera pas les caractères tapés par l'utilisateur.
On aurait pu aussi avoir un type : text pour que le texte s'affiche en clair (pour le login par ex).
Observez attentivement l'url de la page sur laquelle vous êtes arrivés. Que remarquez-vous ?
La méthode GET et la confidentialité :
Les paramètres passés au serveur par la méthode GET sont transmis dans l'url de la requête.
Ils sont donc lisibles en clair par n'importe qui.
Évidemment, c'est une méthode catastrophique pour la transmission des mots de passe.
Par contre, c'est une méthode efficace pour accéder directement à une page particulière : ainsi l'url https://www.google.fr/search?q=bordeaux nous amènera directement au résultat de la recherche Google sur le mot-clé «bordeaux».
2.2 la méthode POST
Dans notre code de formulaire du 1.1, modifions l'attribut method "get" par "post".
Vous pouvez l'excécuter ce nouveau scritp à l'adresse : https://webftts.com/mdp/mdp_post.html
Testez la page sur laquelle vous êtes arrivés.
Que remarquez-vous ?
Les paramètres passés au serveur par la méthode POST ne sont pas visibles dans l'url de la requête.
Ils sont contenus dans le corps de la requête, mais non affichés sur le navigateur.
Vous pouvez le voir en allant sur FireFox, par exmple, en inspectant la page sur Réseau, puis Requête.
La transmission du mot de passe est-elle bien sécurisée par la méthode POST ? Pas du tout ! Si le protocole de transmission est du http et non pas du https, n'importe qui interceptant le trafic peut lire le contenu de la requête et y trouver le mot de passe en clair. Le passage en https chiffre le contenu de la requête et empêche donc la simple lecture du mot de passe.
En résumé :
GET :
La méthode GET doit être utilisée quand les paramètres à envoyer :
- n'ont pas de caractère confidentiel.
- ne sont pas trop longs. En effet, vu qu'ils seront contenus dans l'url, il peut exister des limites de longueur spécifiques au navigateur. Une taille inférieure à 2000 caractère est conseillée. Si vous vous demandez à quoi peuvent servir des url si longues, songez à ce type d'url, (ici PythonTutor) où le code du programme à analyser est contenu dans l'url : http://pythontutor.com/visualize.html#code=L%20%3D%20%5B2,%203,%206,%207,%2011,%2014,%2018,%2019,%2024%5D%0A%0Adef%20trouve_dicho%28L,%20n%29%20%3A%0A%20%20%20%20indice_debut%20%3D%200%0A%20%20%20%20indice_fin%20%3D%20len%28L%29%20-%201%0A%20%20%20%20while%20indice_debut%20%3C%3D%20indice_fin%20%3A%0A%20%20%20%20%20%20%20%20indice_centre%20%3D%20%28indice_debut%20%2B%20indice_fin%29%20//%202%0A%20%20%20%20%20%20%20%20valeur_centrale%20%3D%20L%5Bindice_centre%5D%0A%20%20%20%20%20%20%20%20if%20valeur_centrale%20%3D%3D%20n%20%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20return%20indice_centre%0A%20%20%20%20%20%20%20%20if%20valeur_centrale%20%3C%20n%20%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20indice_debut%20%3D%20indice_centre%20%2B%201%0A%20%20%20%20%20%20%20%20else%20%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20indice_fin%20%3D%20indice_centre%20-%201%0A%20%20%20%20return%20None%0A%0Aprint%28trouve_dicho%28L,14%29%29&cumulative=false&curInstr=0&heapPrimitives=nevernest&mode=display&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false
POST :
La méthode POST doit être utilisée quand les paramètres à envoyer :
- ont un caractère confidentiel (attention, à coupler impérativement avec un protocole de chiffrement).
- peuvent avoir une longueur très importante (le paramètre étant dans le corps de la requête et non plus dans l'url, sa longueur peut être arbitraire). Ainsi, un ordre d'achat sur un site de commerce sera nécessairement passé par une méthode POST.
3. Exercice : attaque par force brute et requête GET
Pré-requis 1 : le module requests en python
Tester l'adresse : https://webftts.com/Images/Waouh.htm
Puis tester le scritp suivant :
import requests
p = requests.get("https://webftts.com/Images/Waouh.htm", verify = False)
print(p.text)Pré-requis 2 : l'extraction d'un fichier texte sous forme de liste
Le code ci-dessous permet de collecter dans une liste mots l'ensemble des mots compris dans le fichier monfichiertexte.txt (si celui-ci comprend un mot par ligne)
mots = open("monfichiertexte.txt").read().splitlines()Exercice :
Votre objectif est de trouver le mot de passe demandé sur la page https://webftts.com/mdp/mdp_get.html
Vous allez utiliser un célèbre ensemble de données contenant des mots de passe qui ont été exposés lors d'une fuite de données, connue sous le nom de fuite 'Rockyou'.
Sur le site piraté, 32 millions de mots de passe étaient enregistrés sans aucune forme de cryptage ou protection.
Quand le site a été piraté, ces 32 millions de mots de passe ont été divulgués sur Internet.
Ils sont désormais disponibles au téléchargement et forment un répertoire de 14 341 564 mots de passe uniques.
Ce nombre est inférieur aux 32 millions initiaux parce que de nombreux utilisateurs avaient des mots de passe identiques.
Le fichier contenant ces mots de passe a une taille considérable de 91,6 Go.
Nous allons utiliser un fichier beaucoup plus léger : 'extraitrockyou.txt', ne contenant que 39 mots de passe : vous le trouverez à
Ici
L'un de ces mots de passe est le mot de passe demandé à la page https://webftts.com/mdp/mdp_get.html.
Lequel ? '¯_(ツ)_/¯'
Solution :
import requests
# URL de la page cible
url = "https://webftts.com/mdp/mdp_cible_get.php?pass="
page_error = requests.get(url).text
# Charger la liste des mots de passe à tester
liste_mdp = open("extraitrockyou.txt").read().splitlines()
# Boucle pour tester chaque mot de passe
for mdp in liste_mdp:
print(mdp)
page_tentative = requests.get(url+mdp).text
#print("{:<15} {:<100}".format(mdp, page_tentative))
# Vérifier si le mot de passe est correct
if page_tentative != page_error:
print()
print("Le mot de passe est le suivant :", mdp)
breakSource : glassus Mille Mercis pour cette ressource.
5.1 - Von Neumann ✔
Architectures matérielles et systèmes d’exploitation
Modèle d’architecture séquentielle (von Neumann)
Capacités attendus :
- Distinguer les rôles et les caractéristiques des différents constituants d’une machine.
- Dérouler l’exécution d’une séquence d’instructions simples du type langage machine.
Commentaires : - La présentation se limite aux concepts généraux.
- On distingue les architectures monoprocesseur et les architectures multiprocesseur.
- Des activités débranchées sont proposées.
- Les circuits combinatoires réalisent des fonctions booléennes
John von Neumann,
né le 28 décembre 1903 à Budapest et mort le 8 février 1957 à Washington, est un mathématicien et physicien américano-hongrois. Il a apporté d'importantes contributions en mécanique quantique, en analyse fonctionnelle, en logique mathématique, en informatique théorique, en sciences économiques et dans beaucoup d'autres domaines des mathématiques et de la physique. Il a de plus participé aux programmes militaires américains.
1. Architecture von Neumann
Cette architecture est appelée ainsi en référence au mathématicien John von Neumann, qui a élaboré en juin 1945 dans le cadre du projet EDVAC la première description d’un ordinateur dont le programme est stocké dans sa mémoire.
Alan Turing, John William Mauchly et John Eckert (pendant leurs travaux sur l’ENIAC) ont également utilisé ce concept ou une idée proche, et ce indépendamment de von Neumann.
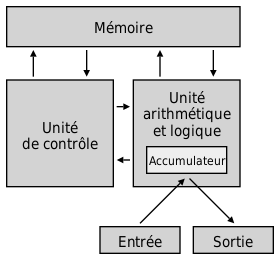
L’architecture de von Neumann décompose l’ordinateur en 4 parties distinctes :
- l’
unité arithmétique et logique(UAL ou ALU en anglais) ou unité de traitement : son rôle est d’effectuer les opérations de base ; - l’
unité de contrôle, chargée du « séquençage » des opérations ; - la
mémoirequi contient à la fois les données et le programme qui indiquera à l’unité de contrôle quels sont les calculs à faire sur ces données. La mémoire se divise entre mémoire volatile (programmes et données en cours de fonctionnement) et mémoire permanente (programmes et données de base de la machine) ; - les
dispositifs d’entrée-sortie, qui permettent de communiquer avec le monde extérieur.
2. Le transistor
On entend souvent dire qu'"un ordinateur utilise uniquement des "1" et des "0"".
À la base de la plupart des composants d'un ordinateur, on retrouve le transistor. Ce composant électronique a été inventé fin 1947 par les Américains John Bardeen, William Shockley et Walter Brattain. L'invention du transistor a été un immense progrès, mais les premiers ordinateurs sont antérieurs à cette invention. En effet, les premiers ordinateurs, par exemple le Colossus qui date de 1943, étaient conçus à base de tubes à vide, beaucoup plus gros et beaucoup moins fiable que les transistors, mais fonctionnent sur le même principe. on ne trouve plus, aujurd'hui, de transistors en tant que composant électronique . Dans un ordinateur, les transistors sont regroupés maintenat au sein de ce que l'on appelle des circuits intégrés. Dans un circuit intégré, les transistors sont gravés sur des plaques de silicium, les connexions entre les millions de transistors qui composent un circuit intégré sont, elles aussi, gravées directement dans le silicium.
Il n'est pas question de nous pencher en détail sur le fonctionnement d'un transistor, mais vous devez tout de même savoir que dans un ordinateur les transistors se comportent comme des interrupteurs : soit le transistor laisse passer le courant électrique (interrupteur fermé), soit il ne le laisse pas passer (interrupteur ouvert).
Et c'est tout, il n'y a pas d'autre état possible pour un transistor dans un ordinateur : le courant passe ou le courant ne passe pas.
Globalement l'ordinateur fonctionne uniquement avec deux états. On parle d'un état "haut" et d'un état "bas". On symbolise souvent l'état "haut" par le chiffre "1" et l'état "bas" par le chiffre "0", mais il faut bien avoir conscience qu'il n'y a pas dans un ordinateur des "petits 1" ou des "petits 0" qui se "baladent", c'est juste une histoire de "courant qui passe" ou de "courant qui ne passe pas". On travaille donc uniquement avec 2 chiffres, voilà pourquoi un ordinateur travaille en base 2 (en binaire) et non pas en base 10 comme dans la vie courante.
Le transistor est l'élément de base des circuits logiques. Un circuit logique permet de réaliser une opération booléenne.
Ces opérations booléennes sont directement liées à l'algèbre de Boole (Georges Boole, mathématicien Britanique 1815-1864) : NOT,AND ,OR, XOR.
Il existe deux catégories de circuit logique :
- les circuits combinatoires (les états en sortie dépendent uniquement des états en entrée)
- les circuits séquentiels (les états en sortie dépendent des états en entrée ainsi que du temps et des états antérieurs)
Dans la suite nous nous intéresserons principalement aux circuits combinatoires.
Les plus simple des circuits combinatoires sont :
En combinant ces circuits logiques, on obtient des circuits plus complexes.
Par exemple en combinant 2 circuit "XOR", 2 "ET" et 1 "OU", on obtient un additionneur, qui Comme son nom l'indique, l'additionneur permet d'additionner 2 bits (E1 et E2) en tenant compte de la retenue entrante ("Cin" "carry in" en anglais).
En sortie on obtient le résultat de l'addition (S) et la retenue sortante ("Cout").
print("S = (E1 XOR E2) XOR Cin et Count = (E1 AND E2) OR ((E1 XOR E2) AND Cin)")
print()
print("E1", "E2", "Cin", "Count", "S", sep="\t")
print("-" * 40)
for E1 in [False, True]:
for E2 in [False, True]:
for Cin in [False, True]:
S = (E1 ^ E2) ^ Cin
Count = (E1 and E2) or ((E1 ^ E2) and Cin)
print(int(E1), int(E2), int(Cin), int(Count), int(S), sep="\t")S = (E1 XOR E2) XOR Cin et Count = (E1 AND E2) OR ((E1 XOR E2) AND Cin) E1 E2 Cin Count S ---------------------------------------- 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1
3. Langage machine
Un ordinateur exécute des programmes qui sont des suites d'instructions.
Le CPU est incapable d'exécuter directement des programmes écrits, par exemple, en Python. En effet, comme tous les autres constituants d'un ordinateur, le CPU gère uniquement 2 états (toujours symbolisés par un "1" et un "0"), les instructions exécutées au niveau du CPU sont donc codées en binaire.
L'ensemble des instructions exécutables directement par le microprocesseur constitue ce que l'on appelle le langage machine.
Une instruction machine est une chaîne binaire composée principalement de 2 parties :
- le champ "code opération" qui indique au processeur le type de traitement à réaliser. Par exemple le code "00100110" donne l'ordre au CPU d'effectuer une multiplication.
- le champ "opérandes" indique la nature des données sur lesquelles l'opération désignée par le "code opération" doit être effectuée.
Il n'est pas question d'apprendre à programmer en assembleur dans ce cours, mais voici tout de même quelques exemples d'instructions en assembleur.
Voici un programme :
x = 4
y = 8
if x == 10:
y = 9
else :
x=x+1
z=6et voici son équivalent en assembleur, essaierez d'établir une correspondance entre les deux :
MOV R0, #4
STR R0,30
MOV R0, #8
STR R0,75
LDR R0,30
CMP R0, #10
BNE else
MOV R0, #9
STR R0,75
B endif
else:
LDR R0,30
ADD R0, R0, #1
STR R0,30
endif:
MOV R0, #6
STR R0,23
HALTAutre exemple :
Voici le même programme en python, en language machine et en binaire.
vidéo : Explication
a = 3
b = 5
c = a + b.pos 0
mrmovl a, %eax
mrmovl b, %ebx
addl %eax, %ebx
rmmovl %ebx, c
halt
.align 4
a: .long 3
b: .long 5
c: .long 0 01010000 00001111 00011000 00000000 00000000 00000000 01010000 00111111 00011100 00000000 00000000 00000000 01100000 00000011 01000000 00111111 00100000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000011 00000000 00000000 00000000 00000101 00000000 00000000 00000000
Le simulateur Y86 permet de simuler la manière dont le processeur va exécuter ce programme.
Vous retrouvez le programme ici.
Dernier exemple utilisation du module numba : ici
5.2 - Réseau 1 ✔
Architectures matérielles et systèmes d’exploitation
Transmission de données dans un réseau
Protocoles de communication
Architecture d’un réseau
Compétences attendues :
- Architecture d’un réseau
- Mettre en évidence l’intérêt du découpage des données en paquets et de leur encapsulation.
- Dérouler le fonctionnement d’un protocole simple de récupération de perte de paquets (bit alterné).
- Simuler ou mettre en œuvre un réseau.
Commentaires :
- Le protocole peut être expliqué et simulé en mode débranché.
- Le lien est fait avec ce qui a été vu en classe de seconde sur le protocole TCP/IP.
- Le rôle des différents constituants du réseau local de l’établissement est présents
1. Premier réseau local
lien de téléchargement de Filius sous windows
lien de téléchargement de Filius sur mon site
Au sein du logiciel Filius, créons le réseau local ci-dessous
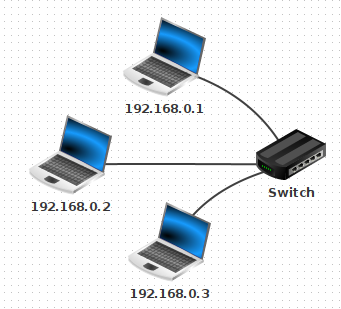
Testons le ping de la machine 192.168.0.1 vers la machine 192.168.0.3 :
1.1. La carte réseau et son adresse MAC
Chaque ordinateur sur le réseau dispose d'une adresse MAC, qui une valeur unique attribuée à sa carte réseau (Ethernet, Wifi, 4G, 5G, ...) lors de sa fabrication en usine.
Cette adresse est codée sur 48 bits, présentés sous la forme de 6 octets en hexadécimal. Exemple : fc:aa:14:75:45:a5
Les trois premiers octets correspondent au code du fabricant. Un site comme https://www.macvendorlookup.com/ vous permet de retrouver le fabricant d'une adresse MAC quelconque.
1.2. Switch, hub, quelle différence ?
Au sein d'un hub Ethernet (de moins en moins vendus), il n'y a aucune analyse des données qui transitent : il s'agit simplement d'un dédoublement des fils de cuivre (tout comme une multiprise électrique). L'intégralité des messages est donc envoyée à l'intégralité des ordinateurs du réseau, même s'ils ne sont pas concernés.
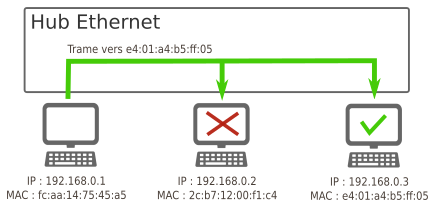Au sein d'un switch Ethernet , une analyse est effectuée sur la trame qui est à distribuer. Lors d'un branchement d'un nouvel ordinateur sur le switch, celui-ci récupère son adresse MAC, ce qui lui permet de trier les messages et de ne les distribuer qu'au bon destinataire.
2. Un deuxième sous-réseau
Rajoutons un deuxième sous-réseau de la manière suivante (penser à bien renommer les switchs).
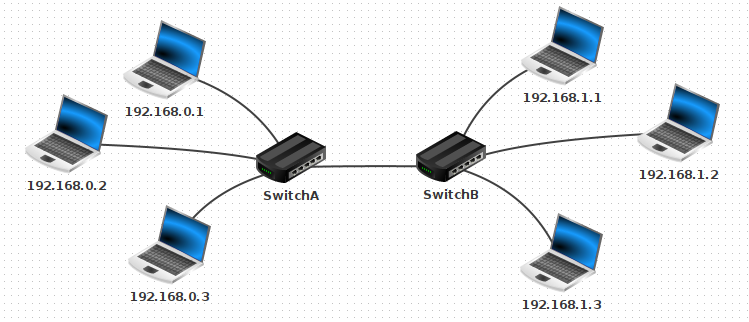
Testons cette hypothèse en essayant de pinger la machine 192.168.1.2 depuis la machine 192.168.0.1.
Cela ne marche pas. L'ordinateur refuse d'envoyer le ping vers la machine 192.168.1.2.
(spoil : car elle n'est pas dans son sous-réseau)
Temporairement, renommons la machine 192.168.1.2 en 192.168.0.33. Testons à nouveau le ping depuis la machine 192.168.0.1.
Cela marche. Les paquets sont bien acheminés.
Intuition : la notion de sous-réseau n'est pas topologique («il suffit de relier les ordinateurs entre eux») mais obéit à des règles numériques.
2.1. Notion de masque de sous-réseau
Dans Filius, lors de l'attribution de l'adresse IP à une machine, une ligne nous permet de spécifier le masque de sous-réseau (appelé simplement « Masque » dans Filius). C'est ce masque qui va permettre de déterminer si une machine appartient à un sous-réseau ou non, en fonction de son adresse IP.
2.1.1 Explication basique
Si le masque est 255.255.255.0, toutes les machines partageant les mêmes trois premiers nombres de leur adresse IP appartiendront au même sous-réseau. Comme ceci est le réglage par défaut de Filius, cela explique pourquoi 192.168.0.33 et 192.168.0.1 sont sur le même sous-réseau, et pourquoi 192.168.1.2 et 192.168.0.1 ne sont pas sur le même sous-réseau.
Dans cette configuration, 256 machines peuvent donc appartenir au même sous-réseau (ce n'est pas tout à fait le cas car des adresses finissant par 0 ou par 255 sont réservées).
Si le masque est 255.255.0.0, toutes les machines partageant les mêmes deux premiers nombres de leur adresse IP appartiendront au même sous-réseau. Dans cette configuration, 65536 machines peuvent être dans le même sous-réseau. (car $256^2=65536$)
Exercice
Renommons 192.168.0.33 en 192.168.1.2 et modifions son masque en 255.255.0.0.
Modifions aussi le masque de 192.168.0.1 en 255.255.0.0.
Testons le ping de 192.168.0.1 vers 192.168.1.2.Résultat du ping
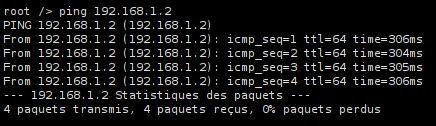
2.1.2 Explication avancée
Lorsqu'une machine A veut envoyer un message à une machine B, elle doit déterminer si cette machine :
- appartient au même sous-réseau : auquel cas le message est envoyé directement via un ou plusieurs switchs.
- n'appartient pas au même sous-réseau : auquel cas le message doit d'abord transiter par un routeur (voir 3.)
Quelle opération permet de distinguer cette appartenance à un même sous-réseau ?
Appelons IP_A et IP_B les adresses IP respectives des machines A et B.
Appelons M le masque de sous-réseau.
Nommons AND l'opérateur de conjonction entre nombres binaires :
Propriété :
A et B appartiennent au même sous-réseau $<=>$ IP_A AND M = IP_B AND M
Deux règles de calcul :
Pour tout octet x, on a : x AND 255 = x et x AND 0 = 0.
Exemple :
Considérons trois machines A, B, C d'IP respectives 192.168.129.10, 192.168.135.200 et 192.168.145.1, configurées avec un masque de sous-réseau égal à 255.255.248.0.
| machine A | machine B | machine C | |
|---|---|---|---|
| IP | 192.168.129.10 | 192.168.135.200 | 192.168.145.1 |
| M | 255.255.248.0 | 255.255.248.0 | 255.255.248.0 |
| IP & M | 192.168.128.0 | 192.168.128.0 | 192.168.144.0 |
129 AND 248 = 10000001 AND 11111000 = 10000000 = 128 en décimal
135 AND 248 = 10000111 AND 11111000 = 10000000 = 128 en décimal
145 AND 248 = 10010001 AND 11111000 = 10010000 = 144 en décimal
Conclusion : les machines A et B sont sous le même sous-réseau, mais pas la machine C.
2.1.3 Cohérence entre les deux explications
Lorsqu'un masque de sous-réseau est égal à 255.255.255.0, l'opération de conjonction & avec chaque IP ne laissera intacts que les 3 premiers octets, le dernier sera égal à 0. Donc si deux adresses s'écrivent A.B.C.X et A.B.C.Y, elles appartiendront forcément au même sous-réseau (typiquement, c'est le cas de 192.168.0.33 et 192.168.0.1).
2.2 Écriture des masques de sous-réseau : notation CIDR
D'après ce qui précède, 2 informations sont nécessaires pour déterminer le sous-réseau auquel appartient une machine : son IP et le masque de sous-réseau. Une convention de notation permet d'écrire simplement ces deux renseignements : la notation CIDR.
Exemple : Une machine d'IP 192.168.0.33 avec un masque de sous-réseau 255.255.255.0 sera désignée par 192.168.0.33 / 24 en notation CIDR.
Le suffixe / 24 signifie que le masque de sous-réseau commence par 24 bits consécutifs de valeur 1 : le reste des bits (donc 8 bits) est à mis à 0.
Autrement dit, ce masque vaut 11111111.11111111.11111111.00000000 , soit 255.255.255.0.
De la même manière, le suffixe / 16 donnera un masque de 11111111.11111111.00000000.00000000 , soit 255.255.0.0. Ou encore, un suffixe / 21 donnera un masque de 11111111.11111111.11111000.00000000 , soit 255.255.248.0.
Exemple :
2.3 Adresses IP :
- Les ordinateurs s'identifient sur les réseaux à l'aide d'une adresse IP (Internet Protocol).
- Suivant la norme IPv4, les adresses IP sont encodées sur 4 octets : on parle d'IPv4.
- Chaque octet pouvant varier de la valeur (décimale) 0 à 255, cela signifie que les adresses IP théoriquement possibles vont de 0.0.0.0 à 255.255.255.255. Il y a donc $256^4 = 4294967296$ adresses possibles. On a longtemps cru que ce nombre serait suffisant. Ce n'est plus le cas, on est donc en train de passer sur des adresses IPv6 à 6 octets (en hexadécimal).
3. Un vrai réseau contenant deux sous-réseaux distincts : la nécessité d'un routeur⚓︎
Notre solution initiale (relier les deux switchs par un cable pour unifier les deux sous-réseaux) n'est pas viable à l'échelle d'un réseau planétaire.
Pour que les machines de deux réseaux différents puissent être connectées, on va utiliser un dispositif équipé de deux cartes réseaux, situé à cheval entre les deux sous-réseaux. Ce équipement de réseau est appelé routeur ou passerelle.
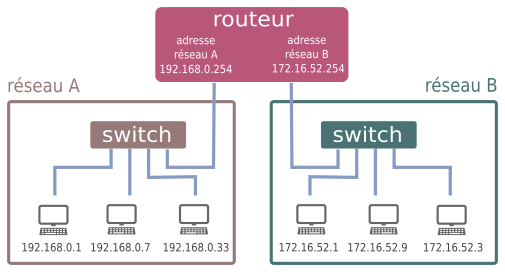
3.1 Principe de fonctionnement
Imaginons que la machine 192.168.0.1 / 24 veuille communiquer avec la machine 172.16.52.3 / 24. L'observation du masque de sous-réseau de la machine 192.168.0.1 / 24 nous apprend qu'elle ne peut communiquer qu'avec les adresses de la forme 192.168.0.X / 24, où X est un nombre entre 0 et 255.
Les 3 étapes du routage :
- Lorsque qu'une machine A veut envoyer un message à une machine B, elle va tout d'abord vérifier si cette machine appartient à son réseau local. si c'est le cas, le message est envoyé par l'intermédiaire du switch qui relie les deux machines.
- Si la machine B n'est pas trouvée sur le réseau local de la machine A, le message va être acheminé vers le routeur, par l'intermédiaire de son adresse de passerelle (qui est bien une adresse appartenant au sous-réseau de A).
- De là, le routeur va regarder si la machine B appartient au deuxième sous-réseau auquel il est connecté. Si c'est le cas, le message est distribué, sinon, le routeur va donner le message à un autre routeur auquel il est connecté et va le charger de distribuer ce message : c'est le procédé (complexe) de routage, qui sera vu en classe de Terminale.
Dans notre exemple, l'adresse 172.16.52.3 n'est pas dans le sous-réseau de 192.168.0.1. Le message va donc transiter par le routeur.
3.2 Illustration avec Filius⚓︎
Rajoutons un routeur entre le SwitchA et le SwitchB.
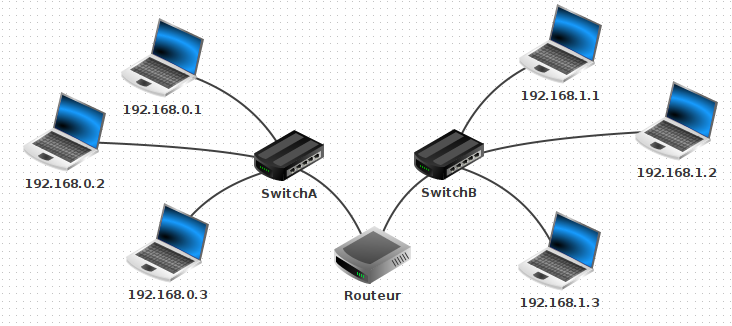
Configuration du routeur : L'interface reliée au Switch A doit avoir une adresse du sous-réseau A. On donne souvent une adresse finissant par 254, qui est en quelque sorte la dernière adresse du réseau (en effet l'adresse en 255 est appelée adresse de broadcast, utilisée pour pinger en une seule fois l'intégralité d'un sous-réseau).
On donne donc l'adresse 192.168.0.254 pour l'interface reliée au Switch A, et 192.168.1.254 pour l'interface reliée au Switch B.
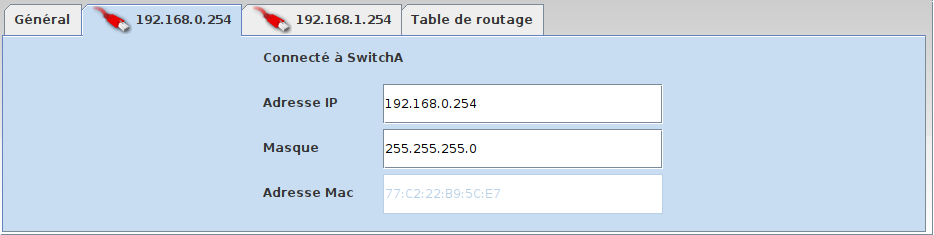
Dans l'onglet général, sélectionner « Routage automatique ». Ainsi configuré notre routeur peut jouer le rôle de passerelle entre les deux sous-réseaux.
Test du ping entre 192.168.0.1 et 192.168.1.2
Cela ne marche pas. La carte réseau refuse d'envoyer les paquets car elle ne sait pas où les envoyer.
Pourquoi cet échec ? Parce que nous devons dire à chaque machine qu'une passerelle est maintenant disponible pour pouvoir sortir de son propre sous-réseau. Il faut donc aller sur la machine 192.168.0.1 et lui donner l'adresse de sa passerelle, qui est 192.168.0.254.
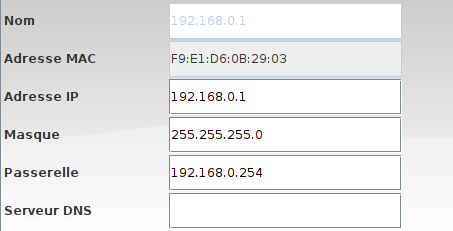
Attention, il faut faire de même pour 192.168.1.2 (avec la bonne passerelle...) Testons à nouveau le ping... Cette fois cela marche.
Plus intéressant : effectuons un traceroute entre 192.168.0.1 et 192.168.1.2.
On y aperçoit que la machine 192.168.1.2 est atteignable en deux sauts depuis 192.168.0.1, en passant par la passerelle 192.168.0.254
Cas d'un réseau domestique
Chez vous, la box de votre opérateur joue simultanément le rôle de switch et de routeur :
- switch car elle répartit la connexion entre les différents dispositifs (ordinateurs branchés en ethernet, smartphone en wifi, tv connectée...)
- routeur car elle fait le lien entre ce sous-réseau domestique (les appareils de votre maison) et le réseau internet.
L'image ci-dessous présente le résultat de la commande ipconfig sous Windows. On y retrouve l'adresse IP locale 192.168.9.103, le masque de sous-réseau 255.255.255.0 et l'adresse de la passerelle 192.168.9.1.
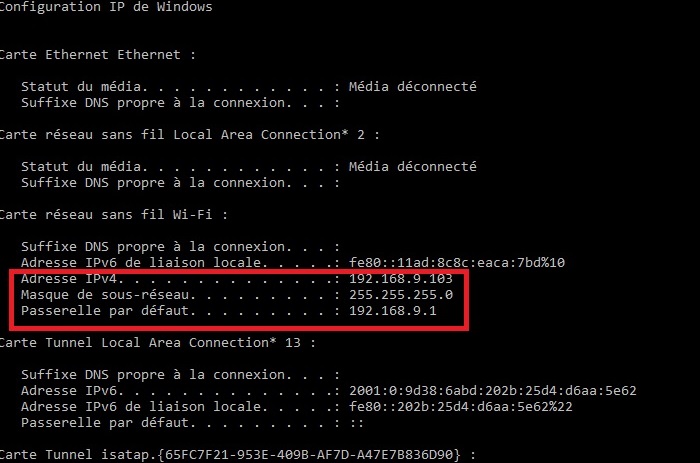
3.3 Annexe : rajout d'un serveur DNS
3.3.1 Rajout d'un serveur web
Connectons un ordinateur au SwitchB, sur l'adresse 192.168.1.30 et installons dessus un Serveur web et démarrons-le.
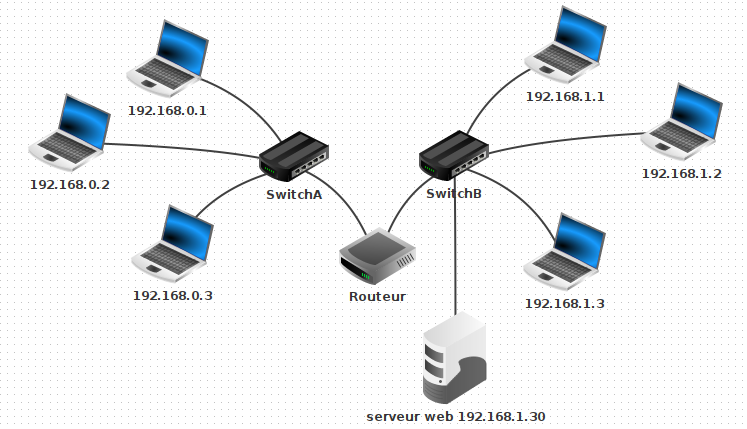
Sur la machine 192.168.0.1, rajoutons un Navigateur Web. En tapant dans la barre d'adresse l'adresse IP du Serveur web, la page d'accueil de Filius s'affiche.
Lors d'une utilisation classique d'un navigateur web, c'est une url mémorisable qui s'affiche, et non une adresse IP : on retient en effet plus facilement https://www.google.com/ que http://216.58.213.131, qui renvoient pourtant à la même adresse. La machine qui assure ce rôle d'annuaire entre les serveurs web et leur adresse IP s'appelle un serveur DNS. Pour pouvoir indexer la totalité des sites internet, son rôle est structuré de manière hiérarchique. Vous trouverez des détails ici
3.3.1 Rajout d'un serveur DNS
Rajoutons un serveur DNS minimal, qui n'aura dans son annuaire d'un seul site. Il faut pour cela raccorder une nouvelle machine (mais une machine déjà sur le réseau aurait très bien pu jouer ce rôle), et installer dessus un serveur DNS.
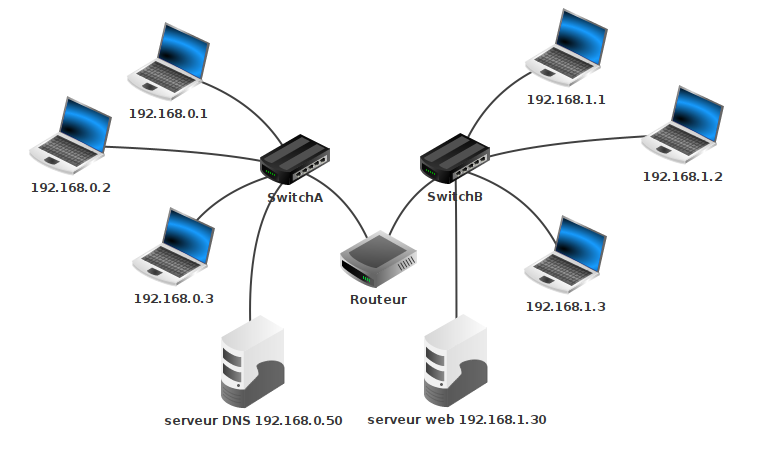
Sur ce serveur DNS, associons l'adresse http://www.vivelansi.fr à l'adresse IP 192.168.1.30.
De retour sur notre machine 192.168.0.1, spécifions maintenant l'adresse du serveur DNS :
Depuis le navigateur web de la machine 192.168.0.1, le site http://www.vivelansi.fr est maintenant accessible.
source : glassus
5.3 - Réseau 2 ✔
Architectures matérielles et systèmes d’exploitation
Suite
Transmission de données dans un réseau
Protocoles de communication
Architecture d’un réseau
Compétences attendues :
- Architecture d’un réseau
- Mettre en évidence l’intérêt du découpage des données en paquets et de leur encapsulation.
- Dérouler le fonctionnement d’un protocole simple de récupération de perte de paquets (bit alterné).
- Simuler ou mettre en œuvre un réseau.
Commentaires :
- Le protocole peut être expliqué et simulé en mode débranché.
- Le lien est fait avec ce qui a été vu en classe de seconde sur le protocole TCP/IP.
- Le rôle des différents constituants du réseau local de l’établissement est présents
1. Modèle OSI, modèle Internet
Les communications réseau reposent sur des protocoles organisés en couches pour garantir l'acheminement et la compréhension des données. Les modèles principaux :
TCP/IP (1974) : 4 couches (liaison, réseau, transport, application).
OSI (1984) : 7 couches (physique, liaison, réseau, transport, session, présentation, application).Les messages traversent les couches à l'envoi et au retour pour être transmis physiquement puis décodés.
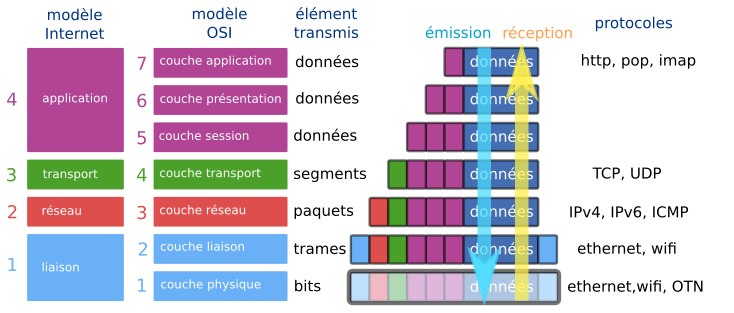
Rôles des couches clés
Application (7-6-5) : Formate les messages pour des protocoles comme HTTP ou FTP.
Transport (4) : Découpe les messages en segments et garantit leur livraison avec TCP.
Réseau (3) : Ajoute des adresses IP pour créer des paquets.
Liaison (2) : Transforme les paquets en trames avec des adresses MAC.
Physique (1) : Transmet les bits via fibre, wifi, ou courant électrique.2. Observation des tram
2.1. Ping à travers un switch
Télécharger le fichier ping_switch.fls.
- Une machine 192.168.0.10 d'adresse MAC BC:81:81:42:9C:31 est reliée à une machine 192.168.0.11 d'adresse MAC 2A:AB:AC:27:D6:A7 à travers un switch. Observons la table SAT de notre switch : elle est vide, car aucune machine n'a encore cherché à communiquer.
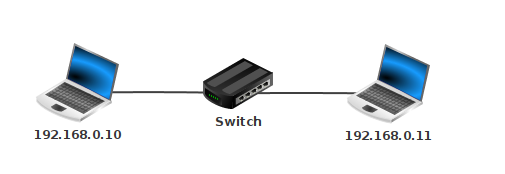
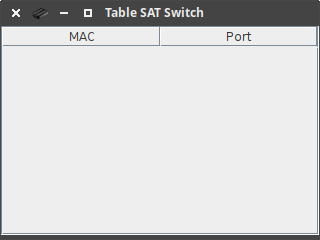
- Lançons un ping depuis 192.168.0.10 vers 192.168.0.11 et observons les données échangées :
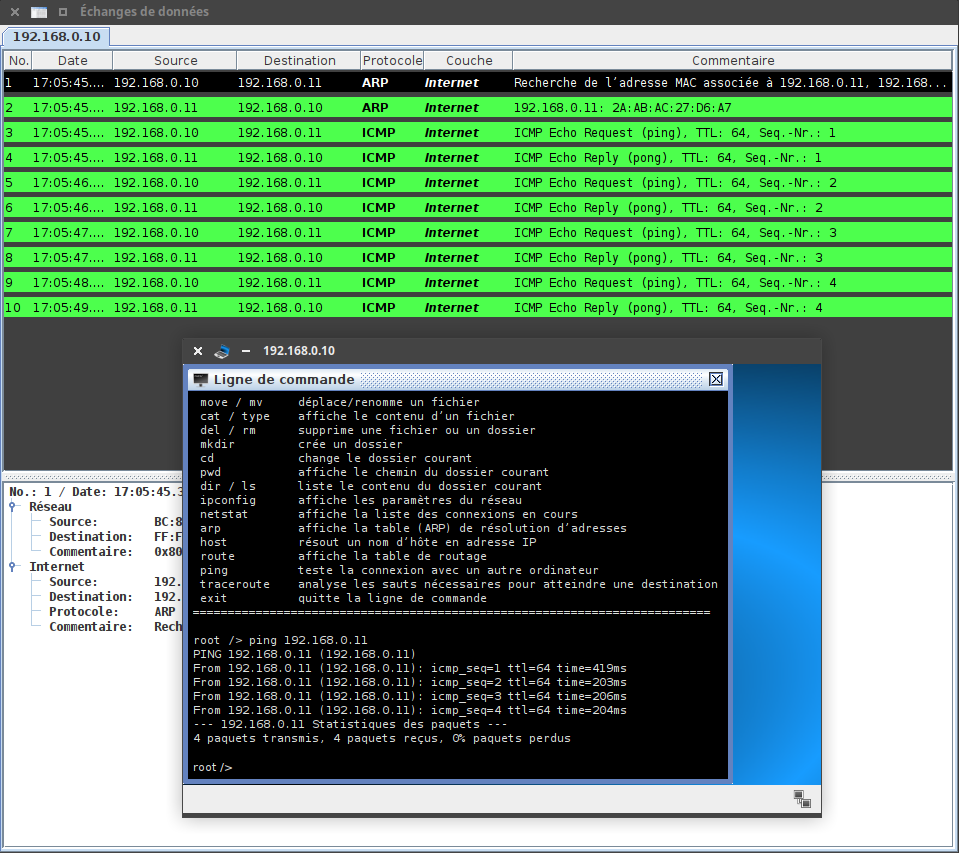
- Observons de plus près la première ligne de données échangées.
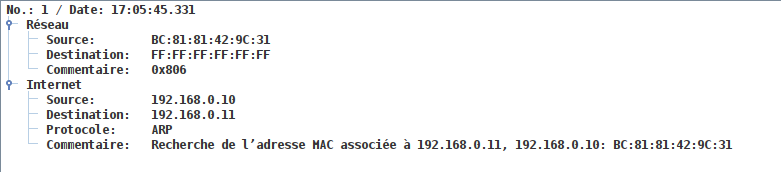
Cette première ligne est une requête ARP. ARP est un protocole qui s'interface entre la couche 3 / réseau (appelée dans la capture d'écran Internet) et la couche 2 / liaison (appelée dans la capture d'écran Réseau). Comme indiqué dans le commentaire, elle consiste à un appel à tout le réseau : "Est-ce que quelqu'un ici possède l'IP 192.168.0.11 ?
Message 1 : « Qui possède l'IP 192.168.0.11 ? »
Il faut comprendre à cette étape que l'adresse IP est totalement inutile pour répérer un ordinateur dans un sous-réseau. Ce sont les adresses MAC qui permettent de se repérer dans un sous-réseau. Les adresses IP, elles, permettront éventuellement d'acheminer le message jusqu'au bon sous-réseau (elles n'intéressent donc que les routeurs).
Revenons à notre ping vers 192.168.0.11.
La commande arp -a effectuée dans un terminal de la machine 192.168.0.10 nous permet de voir qu'elle ne connaît encore personne dans son sous-réseau. La table de correspondance IP ⮀ MAC ne contient que l'adresse de broadcast 255.255.255.255, qui permet d'envoyer un message à tout le réseau.
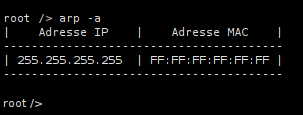
Constatant qu'elle ne sait pas quelle est l'adresse MAC de 192.168.0.11, la machine 192.168.0.10 commence donc par envoyer un message à tout le sous-réseau, par l'adresse MAC de broadcast FF:FF:FF:FF:FF:FF. Le switch va lui aussi lui aussi relayer ce message à tous les équipements qui lui sont connectés (dans notre cas, un seul ordinateur)
Message 2 : « Moi ! »
La machine 192.168.0.11 s'est reconnu dans le message de broadcast de la machine 192.168.0.10. Elle lui répond pour lui donner son adresse MAC.
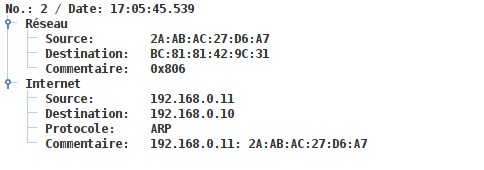
À partir de ce moment, la machine 192.168.0.10 sait comment communiquer avec 192.168.0.11. Elle l'écrit dans sa table arp, afin de ne plus avoir à émettre le message n°1 :
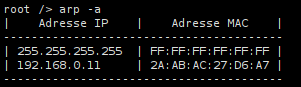
Le switch, qui a vu passer sur ses ports 0 et 1 des messages venant des cartes MAC BC:81:81:42:9C:31 et 2A:AB:AC:27:D6:A7, peut mettre à jour sa table SAT :
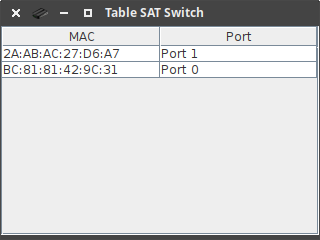
Par la suite, il saura sur quel port rediriger les messages destinés à ces deux adresses MAC. Un switch est un équipement de réseau de la couche 2 du modèle OSI, il ne sait pas lire les adresses IP : il ne travaille qu'avec les adresses MAC.
Message 3 : le ping est envoyé
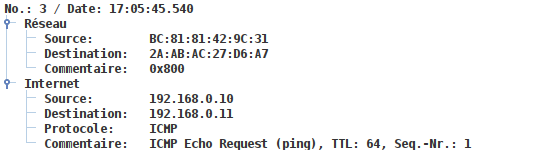
Schématisons cette trame Ethernet (couche 2 du modèle OSI) :
Message 4 : le pong est retourné
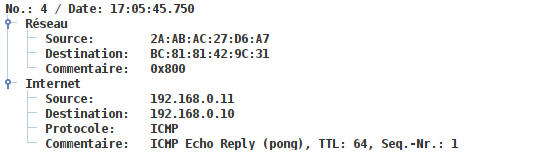
2.2. Ping à travers un routeur
Télécharger le fichier ping_routeur.fls.
L'objectif est d'observer les trames lors d'un ping entre :
- l'ordinateur du réeau A :
- IP : 192.168.0.1
- MAC : F9:E1:D6:0B:29:03
- et l'ordinateur du réseau B :
- IP : 192.168.1.1
- MAC D3:79:96:B8:5C:A4
Le routeur est configuré ainsi :
- interface sur le réseau A :
- IP : 192.168.0.254
- MAC : 77:C2:22:C9:5C:E7
- interface sur le réseau B :
- IP : 192.168.1.254
- MAC : 66:E5:4E:7D:0B:B0
Étape 0 : le routeur signale sa présence
Lors de l'observation des 2 messages émis à tous par le routeur sur les reseaux A et B, on peut être intrigué :
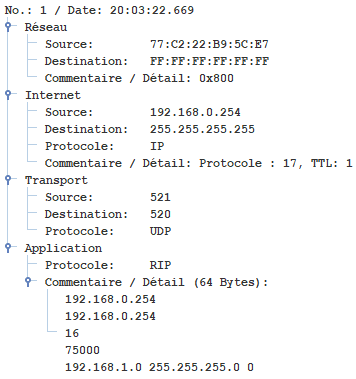
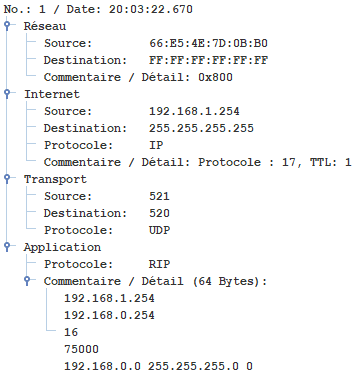
On peut y distinguer les 4 couches du modèle Internet.
Le routeur, par ces 2 pour déclare sa présence, et le fait qu'il possède deux interfaces 192.168.1.254 et 192.168.0.254, une pour chaque réseau.
Il se positionne ainsi comme une passerelle entre les 2 sous-réseaux.
Dans ces trame envoyée figure ses adresses MAC 77:C2:22:B9:5C:E7 et 66:E5:4E:7D:0B:B0, de sorte que tous les membres de son sous-réseau pourront donc communiquer avec lui.
Étape 1 : de 192.168.0.1 vers le routeur
La machine 192.168.0.1 conprends que la machine 192.168.1.1 avec laquelle elle veut communiquer n'est pas dans son sous-réseau. Elle va donc envoyer son message à sa passerelle, qui est l'adresse du routeur dans son sous-réseau.
Cette première trame est :
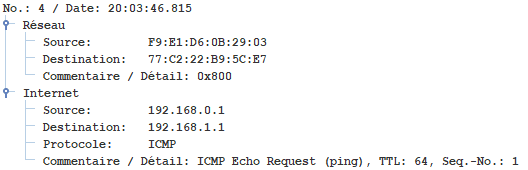
Étape 2 : le routeur décapsule la trame
Le routeur est un équipement de réseau de couche 3 (couche réseau).
Il doit observer le contenu du paquet IP, sans remonter jusqu'au contenu du message, pour savoir, suivant le procédé de routage, où acheminer ce paquet.
Dans notre cas, l'adresse IP 192.168.1.1 de destination lui est accessible, elle fait partie de son sous-réseau B.
Le routeur va modifier la valeur du TTL (Time To Live), en la décrémentant de 1. Si, après de multiples routages, cette valeur devenait égale à 0, ce paquet serait détruit. Ceci a pour but d'éviter l'encombrement des réseaux avec des paquets ne trouvant pas leur destination.
Le routeur va ré-encapsuler le paquet IP modifié, et créer une nouvelle trame Ethernet en modifiant :
- l'adresse MAC source : il va mettre l'adresse MAC de son interface dans le sous-réseau B.
- l'adresse MAC de destination : il va mettre l'adresse MAC de 192.168.1.1 qu'il aura peut-être récupérée au préalable par le protocole ARP.
On peut observer dans Filius cette trame, en se positionnant sur l'interface 192.168.1.254 du routeur, ou sur 192.168.1.1 :
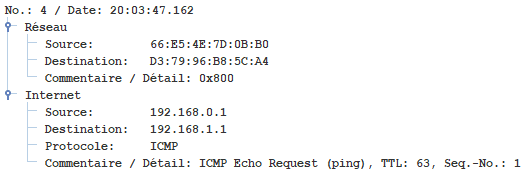
3. Protocole du bit alterné
Ce protocole est un exemple simple de fiabilisation du transfert de données.
1. Contexte
- Alice veut envoyer à Bob un message M, qu'elle a prédécoupé en sous-messages M0, M1, M2,...
- Alice envoie ses sous-messages à une cadence Δt fixée (en pratique, les sous-messages partent quand leur acquittement a été reçu ou qu'on a attendu celui-ci trop longtemps : on parle alors de timeout)
2. Situation idéale
Dans cette situation, les sous-messages arrivent tous à destination dans le bon ordre. La transmission est correcte.
3. Situation réelle
Mais parfois, les choses ne se passent pas toujours aussi bien. Car si on maîtrise parfaitement le timing de l'envoi des sous-messages d'Alice, on ne sait pas combien de temps vont mettre ces sous-messages pour arriver, ni même (attention je vais passer dans un tunnel) s'ils ne vont pas être détruits en route.
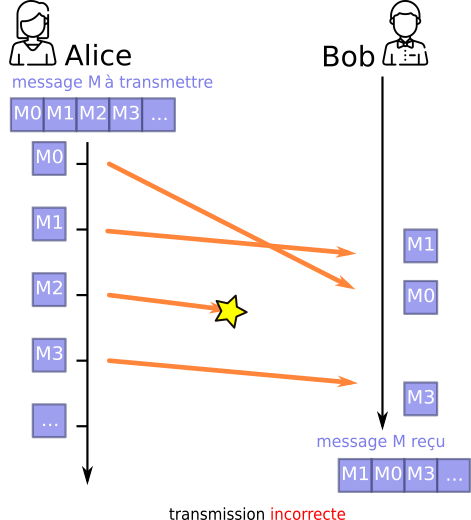
Le sous-message M0 est arrivé après le M1, le message M2 n'est jamais arrivé...
Que faire ?
Écartons l'idée de numéroter les sous-messages, afin que Bob puisse remettre dans l'ordre les messages arrivés, ou même redemander spécifiquement des sous-messages perdus. C'est ce que réalise le protocole TCP (couche 4 — transport), c'est très efficace, mais cher en ressources. Essayons de trouver une solution plus basique.
3. Solution naïve...
Pourquoi ne pas demander à Bob d'envoyer un signal pour dire à Alice qu'il vient bien de recevoir son sous-message ? Nous appelerons ce signal ACK (comme acknowledgement, traduisible par «accusé de réception»). Ce signal ACK permettra à Alice de renvoyer un message qu'elle considérera comme perdu :
N'ayant pas reçu le ACK consécutif à son message M1, Alice suppose (avec raison) que ce message n'est pas parvenu jusqu'à Bob, et donc renvoie le message M1.
4. Mais peu efficace...
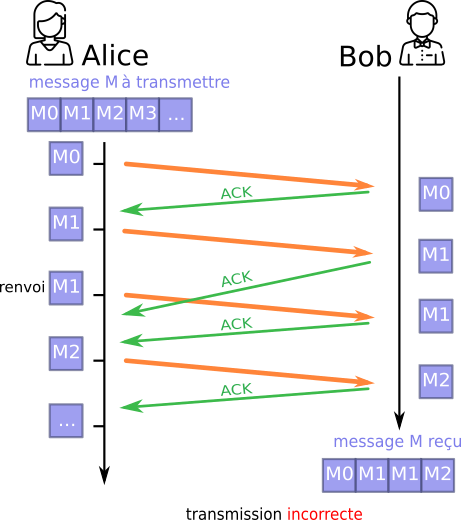
Le deuxième ACK de Bob a mis trop de temps pour arriver (ou s'est perdu en route) et donc Alice a supposé que son sous-message M1 n'était pas arrivé. Elle l'a donc renvoyé, et Bob se retrouve avec deux fois le sous-message M1. La transmission est incorrecte. En faisant transiter un message entre Bob et Alice, nous multiplions par 2 la probabilité que des problèmes techniques de transmission interviennent. Et pour l'instant rien ne nous permet de les détecter.
5. Bob prend le contrôle
Bob va maintenant intégrer une méthode de validation du sous-message reçu. Il pourra décider de le garder ou de l'écarter. Le but est d'éviter les doublons.
Pour réaliser ceci, Alice va rajouter à chacun de ses sous-messages un bit de contrôle, que nous appelerons FLAG (drapeau). Au départ, ce FLAG vaut 0. Quand Bob reçoit un FLAG, il renvoie un ACK égal au FLAG reçu.
Alice va attendre ce ACK contenant le même bit que son dernier FLAG envoyé :
- tant qu'elle ne l'aura pas reçu, elle continuera à envoyer le même sous-message, avec le même FLAG.
- dès qu'elle l'a reçu, elle peut envoyer un nouveau sous-message en inversant («alternant») le bit de son dernier FLAG (d'où le nom de ce protocole).
Bob, de son côté, va contrôler la validité de ce qu'il reçoit : il ne gardera que les sous-messages dont le FLAG est égal à l'inverse de son dernier ACK. C'est cette méthode qui lui permettra d'écarter les doublons.
Observons ce protocole dans plusieurs cas :
5.1 Cas où le sous-message est perdu
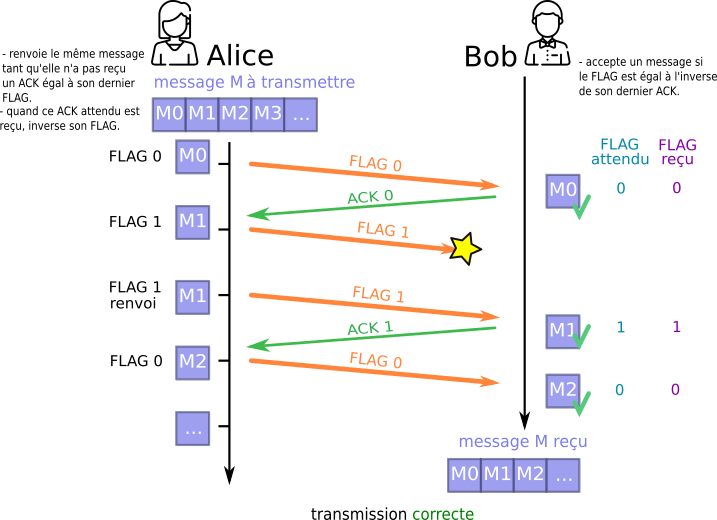
5.2 Cas où le ACK est perdu
Le protocole a bien détecté le doublon du sous-message M1.
5.3 Cas où un sous-message est en retard
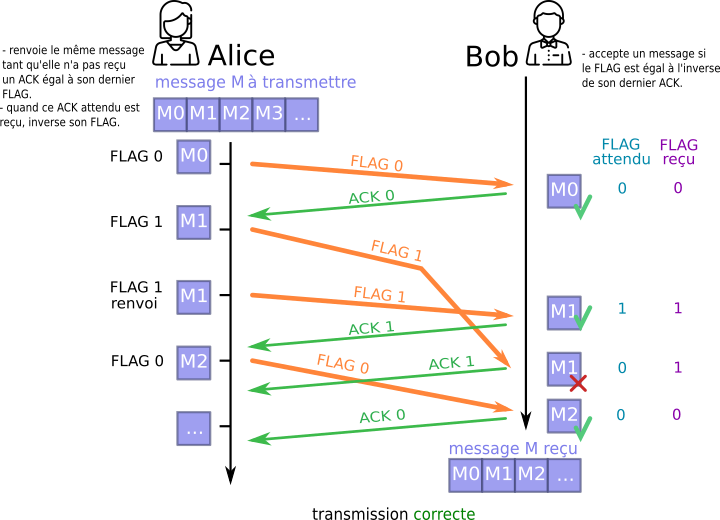
Le protocole a bien détecté le doublon du sous-message M1... mais que se passerait-il si notre premier sous-message M1 était encore plus en retard ?
6. Conclusion
Le protocole du bit alterné a longtemps été utilisé au sein de la couche 2 du modèle OSI (distribution des trames Ethernet). Simple et léger, il peut toutefois être facilement mis en défaut, ce qui explique qu'il ait été remplacé par des protocoles plus performants.
source : glassus
5.4 - OS ✔
Architectures matérielles et systèmes d’exploitation
Systèmes d’exploitation
Capacités Attendue :
- Identifier les fonctions d’un système d’exploitation.
- Utiliser les commandes de base en ligne de commande.
- Gérer les droits et permissions d’accès aux fichiers.
Commentaires :
- Les différences entre systèmes d’exploitation libres et propriétaires sont évoquées.
- Les élèves utilisent un système d’exploitation libre.
- Il ne s’agit pas d’une étude théorique des systèmes d’exploitation.
Un système d'exploitation (SE) est un logiciel qui agit comme un intermédiaire entre l'ordinateur matériel et les applications logicielles. Ses principales fonctions sont la gestion des ressources matérielles et la fourniture d'une interface utilisateur. Voici les principales fonctions d'un SE :
- Gestion des ressources matérielles : Le SE gère les ressources telles que le processeur, la mémoire, le stockage et les périphériques pour garantir une utilisation efficace.
- Interface utilisateur : Il offre une interface conviviale pour les utilisateurs, qui peut être en mode graphique ou en ligne de commande.
- Gestion des fichiers et des répertoires : Les SE permettent la création, la modification, la suppression et la gestion des fichiers et des répertoires.
- Contrôle des accès : Les droits et les permissions d'accès aux fichiers sont gérés pour garantir la sécurité et la confidentialité des données.
- Gestion des processus : Les SE permettent l'exécution de plusieurs processus en parallèle, les surveillent et les planifient pour optimiser les ressources.
- Gestion de la mémoire : Ils allouent et désallouent de la mémoire aux processus en cours d'exécution.
1. Utilisation des Commandes en Ligne de Commande
Dans un système d'exploitation basé sur Unix/Linux, l'utilisation des commandes en ligne de commande est essentielle.
Voici quelques commandes de base :
ls : Affiche la liste des fichiers et répertoires dans le répertoire courant.
Exemple : ls
cd : Pour changer de répertoire.
Exemple : cd /chemin/vers/le/nouveau/dossier (Remplacez "/chemin/vers/le/nouveau/dossier" par le chemin du répertoire que vous souhaitez rejoindre)
mkdir : Crée un nouveau répertoire.
Exemple : mkdir NouveauDossier (Crée un dossier nommé "NouveauDossier" dans le répertoire courant)
echo : Cette commande permet d'afficher du texte à l'écran.
Exemple : echo Bonjour, monde
cp : Copier des fichiers.
Exemple : cp fichier1.txt DossierDestination (Copie "fichier1.txt" dans "DossierDestination")
mv : Déplacer des fichiers ou des répertoires vers un autre emplacement.
Exemple : mv fichier.txt DossierDestination (Déplace "fichier.txt" dans "DossierDestination")
rm : Supprime un fichier.
Exemple : rm fichier.txt (Supprime le fichier "fichier.txt")
rmdir : Supprime un répertoire vide.
Exemple : rmdir DossierVide (Supprime le répertoire "DossierVide")
ifconfig : Affiche les informations de configuration réseau de votre système.
Exemple : ifconfig
ps : Liste les processus en cours d'exécution.
Exemple : ps aux
kill : Met fin à un processus en cours d'exécution. Vous aurez besoin de spécifier le PID (identifiant du processus).
Exemple : kill -9 PID (Remplacez "PID" par l'identifiant du processus que vous souhaitez arrêter)
uname : Affiche des informations détaillées sur votre système, y compris la version du noyau Linux.
Exemple : uname -a
shutdown : Éteindre ou redémarrer l'ordinateur.
Exemple : sudo shutdown -h now (Éteindra l'ordinateur)
fsck : Vérifie et répare les erreurs sur un système de fichiers.
Exemple : fsck -f /dev/sda1 (Vérifiera le système de fichiers sur la partition /dev/sda1)
sudo apt-get update : Met à jour la liste des paquets disponibles dans les dépôts de logiciels.
Exemple : sudo apt-get update
useradd : Permet de créer un nouvel utilisateur.
Exemple : sudo useradd nouvel_utilisateur
chmod : Modifie les permissions d'accès aux fichiers.
Exemple : chmod 755 fichier.txt (Accorde des permissions de lecture, écriture et exécution au propriétaire, et des permissions de lecture aux autres)
df : Affiche des informations sur l'utilisation de l'espace disque.
Exemple : df -h (Affiche les informations en format lisible par l'homme)
clear : Efface le contenu de l'écran de la console pour le rendre plus propre.
Exemple : clearNotez également que certaines commandes, comme sudo, nécessitent des privilèges d'administration pour être exécutées.
Pour Windows en ligne de commande (Invite de commandes ou PowerShell) :
dir : Affiche la liste des fichiers et répertoires dans le répertoire courant.
Exemple : dir
cd : Pour changer de répertoire.
Exemple : cd CheminDuNouveauDossier (Remplacez "CheminDuNouveauDossier" par le chemin du répertoire que vous souhaitez rejoindre)
mkdir : Crée un nouveau répertoire.
Exemple : mkdir NouveauDossier (Crée un dossier nommé "NouveauDossier" dans le répertoire courant)
echo : Cette commande permet d'afficher du texte à l'écran.
Exemple : echo Bonjour, monde
copy : Copier des fichiers.
Exemple : copy fichier1.txt DossierDestination (Copie "fichier1.txt" dans "DossierDestination")
move : Déplacer des fichiers ou des répertoires vers un autre emplacement.
Exemple : move fichier.txt DossierDestination (Déplace "fichier.txt" dans "DossierDestination")
del ou erase : Supprime un fichier.
Exemple : del fichier.txt (Supprime le fichier "fichier.txt")
rmdir : Supprime un répertoire vide.
Exemple : rmdir DossierVide (Supprime le répertoire "DossierVide")
ipconfig : Affiche les informations de configuration réseau de votre système.
Exemple : ipconfig
tasklist : Liste les processus en cours d'exécution.
Exemple : tasklist
taskkill : Met fin à un processus en cours d'exécution. Vous aurez besoin de spécifier le nom ou l'ID du processus.
Exemple : taskkill /IM nomDuProcessus.exe (Remplacez "nomDuProcessus.exe" par le nom du processus que vous souhaitez arrêter)
systeminfo : Affiche des informations détaillées sur votre système, y compris la version de Windows, la mémoire RAM, etc.
Exemple : systeminfo
shutdown : Éteindre ou redémarrer l'ordinateur.
Exemple : shutdown /s (Éteindra l'ordinateur)
sfc /scannow : Exécute une analyse du système pour rechercher et réparer les fichiers système corrompus.
Exemple : sfc /scannow
gpupdate /force : Force la mise à jour des stratégies de groupe.
Exemple : gpupdate /force
net : Gérer divers aspects du réseau et des utilisateurs, tels que "net user" pour gérer les comptes d'utilisateurs.
Exemple : net user (Affichera la liste des comptes d'utilisateurs)
chkdsk : Vérifie et répare les erreurs sur un lecteur de disque.
Exemple : chkdsk C: (Vérifiera le lecteur C:)
wmic : Permet d'accéder à une grande variété d'informations système et de les manipuler.
Exemple : wmic os get Caption (Affichera le nom du système d'exploitation)
cls : Efface le contenu de l'écran de la console pour le rendre plus propre.
Exemple : clsCes commandes sont très utiles pour effectuer diverses tâches de gestion et de dépannage sous Windows en utilisant l'invite de commandes ou PowerShell. Vous pouvez taper help suivi du nom d'une commande pour obtenir de l'aide détaillée sur son utilisation.
2. Différences entre Systèmes d'Exploitation Libres et Propriétaires
Les systèmes d'exploitation libres, tels que Linux, offrent les avantages suivants :
Ils sont généralement gratuits.
Ils sont open source, ce qui signifie que leur code source est disponible pour être examiné, modifié et distribué.
Ils sont souvent plus stables et sécurisés en raison de la collaboration communautaire.Les systèmes d'exploitation propriétaires, tels que Windows, ont des avantages tels que :
Un support commercial disponible.
Une compatibilité avec un large éventail de logiciels et de matériel.
Une interface utilisateur plus conviviale pour les débutants.Cependant, ils peuvent être coûteux et moins personnalisables que les systèmes libres.
3. Gérer les droits et les permissions d'accès aux fichiers
Gérer les droits et les permissions d'accès aux fichiers est une partie essentielle de l'administration d'un système d'exploitation, que ce soit sous Windows ou Linux. Les droits et les permissions permettent de contrôler qui peut accéder aux fichiers, qui peut les modifier, et qui peut les exécuter. Voici comment cela fonctionne en détail pour les deux systèmes d'exploitation :
Sous Linux :
Linux utilise un système de gestion des droits et des permissions basé sur des utilisateurs et des groupes. Chaque fichier et répertoire est associé à un propriétaire et à un groupe, et il existe trois types de permissions : lecture (r), écriture (w), et exécution (x). Voici comment gérer les droits et les permissions sous Linux :
Changer de propriétaire et de groupe : La commande chown permet de changer le propriétaire et le groupe d'un fichier ou d'un répertoire. Par exemple, pour changer le propriétaire d'un fichier en "nouveau_proprietaire" et le groupe en "nouveau_groupe", vous pouvez utiliser : chown nouveau_proprietaire:nouveau_groupe fichier.txt.
Modifier les permissions : La commande chmod est utilisée pour modifier les permissions d'un fichier ou d'un répertoire. Par exemple, chmod u+rwx fichier.txt accorde au propriétaire les droits de lecture, écriture et exécution sur "fichier.txt".
Gérer les groupes : Vous pouvez ajouter un utilisateur à un groupe en utilisant la commande usermod. Par exemple, pour ajouter un utilisateur à un groupe "mon_groupe", vous pouvez faire : usermod -aG mon_groupe utilisateur.
Lister les permissions : Utilisez la commande ls -l pour afficher les permissions de fichiers et de répertoires dans un format lisible. Vous verrez une sortie similaire à ceci : -rw-r--r-- 1 utilisateur groupe 1000 oct. 30 10:00 fichier.txt
Utiliser sudo : Pour effectuer des opérations de gestion de fichiers qui nécessitent des privilèges d'administration, utilisez la commande sudo pour exécuter des commandes en tant que superutilisateur.Sous Windows :
Windows utilise un modèle de contrôle d'accès basé sur des listes de contrôle d'accès (ACL) pour gérer les droits et les permissions. Voici comment gérer les droits et les permissions sous Windows :
Changer de propriétaire : Cliquez avec le bouton droit sur un fichier ou un répertoire, sélectionnez "Propriétés," allez dans l'onglet "Sécurité," puis cliquez sur "Avancé." Vous pouvez changer le propriétaire sous l'onglet "Propriétaire."
Modifier les autorisations : Dans l'onglet "Sécurité" des propriétés du fichier, cliquez sur "Modifier" pour ajuster les autorisations. Vous pouvez ajouter, supprimer ou modifier les autorisations pour les utilisateurs et les groupes.
Groupes d'utilisateurs : Windows utilise des groupes d'utilisateurs pour simplifier la gestion des autorisations. Vous pouvez ajouter des utilisateurs à des groupes spécifiques pour définir des autorisations en bloc.
Héritage des autorisations : Par défaut, les sous-répertoires et fichiers héritent des autorisations du répertoire parent. Vous pouvez désactiver l'héritage et spécifier des autorisations spécifiques pour chaque fichier ou répertoire.
Contrôle d'accès aux objets système (SACL) : Vous pouvez surveiller et auditer les accès aux fichiers en configurant des SACL, ce qui est utile pour la sécurité et la conformité.En résumé, la gestion des droits et des permissions d'accès aux fichiers sous Windows et Linux est essentielle pour garantir la sécurité, la confidentialité et la gestion efficace des fichiers et des répertoires. Les commandes et les méthodes varient entre les deux systèmes, mais le principe fondamental est de définir qui peut faire quoi avec un fichier ou un répertoire.
5.5 - Périphériques ✔
Architectures matérielles et systèmes d’exploitation
Périphériques d’entrée et de sortie, Interface Homme-Machine (IHM)
Capacités Attendue :
- Identifier le rôle des capteurs et actionneurs.
- Réaliser par programmation une IHM répondant à un cahier des charges donné.
Commentaires :
Les activités peuvent être développées sur des objets connectés, des systèmes embarqués ou robots.
1. Périphériques d'entrée et de sortie :
Les périphériques d'entrée sont des dispositifs qui permettent aux utilisateurs d'envoyer des informations à un système informatique. Les exemples courants incluent le clavier, la souris, le microphone, le scanner, etc. Ces dispositifs sont essentiels pour entrer des données dans un ordinateur.
Les périphériques de sortie, quant à eux, sont des dispositifs qui permettent au système informatique de transmettre des informations à l'utilisateur. Les exemples courants incluent l'écran, l'imprimante, les haut-parleurs, etc. Ils sont responsables de l'affichage ou de la restitution des résultats ou des données traitées par l'ordinateur.
Interface Homme-Machine (IHM) : L'IHM est la zone de communication entre un utilisateur et un système informatique. Elle vise à rendre cette interaction aussi conviviale que possible. Les éléments clés d'une IHM incluent les fenêtres, les boutons, les icônes, les menus déroulants, etc. Une bonne IHM devrait être intuitive, facile à comprendre et à utiliser.
2. Rôle des capteurs et actionneurs :
-
Capteurs : Les capteurs sont des dispositifs qui mesurent des grandeurs physiques, telles que la température, la pression, la lumière, le mouvement, etc. Ils convertissent ces grandeurs en signaux électriques ou numériques que l'ordinateur peut comprendre. Les capteurs sont utilisés pour collecter des données de l'environnement.
-
Actionneurs : Les actionneurs sont des dispositifs qui agissent en réponse aux commandes de l'ordinateur. Ils transforment les signaux électriques ou numériques en actions physiques. Par exemple, un moteur est un actionneur qui peut tourner ou déplacer quelque chose en réponse à une commande.
3. Réalisation d'une IHM par programmation :
Pour créer une IHM répondant à un cahier des charges donné, vous pouvez utiliser des langages de programmation adaptés à cet objectif, tels que Python avec des bibliothèques graphiques comme Tkinter ou PyQt. Voici les étapes générales à suivre :
-
Conception de l'IHM : Identifiez les besoins de votre cahier des charges et concevez l'interface utilisateur en plaçant les éléments nécessaires (boutons, zones de texte, etc.) à l'aide de la bibliothèque graphique choisie.
-
Programmation : Écrivez le code pour créer les éléments de l'IHM et définissez leurs comportements en réponse aux actions de l'utilisateur. Par exemple, vous pouvez définir ce qui se passe lorsque l'utilisateur clique sur un bouton.
-
Intégration avec Capteurs/Actionneurs : Si votre projet nécessite l'utilisation de capteurs et d'actionneurs, assurez-vous que votre programme peut interagir avec eux. Vous devrez peut-être utiliser des bibliothèques spécifiques pour cela.
-
Test et Validation : Testez votre IHM pour vous assurer qu'elle répond aux spécifications du cahier des charges. Effectuez des ajustements si nécessaire.
-
Documentation : Documentez votre code et votre IHM pour faciliter la maintenance future.
-
Déploiement : Une fois que tout fonctionne comme prévu, déployez votre IHM sur l'appareil ou le système cible.
N'oubliez pas de consulter la documentation de la bibliothèque graphique que vous utilisez, car elle fournira des instructions spécifiques pour créer des IHMs avec le langage de programmation choisi.
Voici un exemple de code pour une calculatrice basique en utilisant la bibliothèque Tkinter en Python :
import tkinter as tk
# Fonction pour ajouter un chiffre ou un opérateur à l'entrée
def append_text(value):
entry.insert(tk.END, value)
# Fonction pour effacer l'entrée
def clear():
entry.delete(0, tk.END)
# Fonction pour évaluer l'expression et afficher le résultat
def calculate():
try:
result = eval(entry.get())
entry.delete(0, tk.END)
entry.insert(tk.END, str(result))
except:
entry.delete(0, tk.END)
entry.insert(tk.END, "Erreur")
# Création de la fenêtre principale
root = tk.Tk()
root.title("Calculatrice Simple")
# Création de la zone de texte d'entrée
entry = tk.Entry(root, width=20)
entry.grid(row=0, column=0, columnspan=4)
# Création des boutons pour les chiffres et opérateurs
buttons = [
'7', '8', '9', '/',
'4', '5', '6', '*',
'1', '2', '3', '-',
'0', '.', '=', '+'
]
row_val = 1
col_val = 0
for button in buttons:
tk.Button(root, text=button, padx=20, pady=20, command=lambda b=button: append_text(b) if b != '=' else calculate()).grid(row=row_val, column=col_val)
col_val += 1
if col_val > 3:
col_val = 0
row_val += 1
# Bouton pour effacer l'entrée
tk.Button(root, text='C', padx=20, pady=20, command=clear).grid(row=row_val, column=col_val)
# Lancement de la boucle principale
root.mainloop()6.0 - Elémentaires ✔
Exercices : NSI - Première - Construction élémentaires
Capacités attendues : Mettre en évidence un corpus de constructions élémentaires.
Commentaires : Séquences, affectation,conditionnelles, boucles bornées,boucles non bornées, appels de fonction.
De variables à conditions
Exercice 1 :
Ecrire un programme qui demande votre prénom et affiche "Bonjour Arthur", si la réponse est Arthur
Exercice 2 :
Ecrire un programme qui demande 2 nombres entiers et affiche leur somme et leur produit avec une phrase du genre le produit de 3 et 5 est 15, leur somme est 8.
Exercice 3 :
idem que l'exercice 2, mais avec des nombres décimaux.
Exercice 4 :
Ecrire un programme qui demande deux nombres et qui dit "la somme est bien 100" ou "la somme ne fait pas 100".
Exercice 5:
Ecrire un programme qui demande un prénom et qui dit "Bonjour Paul" ou "Bonjour, je croyais que c'était Paul".
Exercice 6:
Convertir une note scolaire N quelconque, entrée par l’utilisateur sous forme de points (par exemple 27 sur 85), en une note standardisée suivant le code ci-dessous : Note N Appréciation N >= 80 % A 80 % > N >= 60 % B 60 % > N >= 50 % C 50 % > N >= 40 % D N < 40 % E
Boucles bornées
Exercice 7:
Ecrire un programme qui affiche les carrés des entiers de 1 à 7 ?
Exercice 8:
Écrire les nombres pairs jusqu'à 20.
Exercice 9:
Écrire un programme qui affiche les 20 premiers produits de la table de multiplication de 7.
Exercice 10:
Écrire un programme qui affiche une suite de 12 nombres dont chaque terme soit égal au double du terme précédent.
Exercice 11:
Écrire un programme qui affiche les 20 premiers termes de la table de multiplication par 7, en signalant au passage (a l’aide d’une astérisque) ceux qui sont des multiples de 3.
Exercice 11:
Écrire un programme qui calcule les 50 premiers termes de la table de multiplication par 13, mais n’affiche que ceux qui sont des multiples de 7.
Exercice 12:
Ecrire un programme qui affiche la somme des premiers entiers jusqu'à 30.
Boucles non bornées
Exercice 13:
Ecrire un programme qui demande un prénom. Si ce prénom est Paul, le programme affiche "enfin c'est toi", sinon le programme redemande un nouveau prénom car ce n'est pas la personne qu'il attend.
Exercice 14:
Ecrire un programme qui additionne tous les nombres que vous entrez (tour à tour) et qui s'arrête lorsque vous tapez 0.
Exercice 15:
Ecrire un programme qui additionne tous les nombres que vous entrez (tour à tour) et qui s'arrête lorsque la somme dépasse 100.
Fonctions
Exercice 16:
Écrire une fonction qui calcule le volume d’un parallélépipède rectangle dont sont fournis au départ la largeur, la hauteur et la profondeur. Testez votre fonction.
Exercice 17:
Déterminer si une année (dont le millésime est introduit par l’utilisateur) est bissextile ou non. Une année A est bissextile si A est divisible par 4. Elle ne l’est cependant pas si A est un multiple de 100, a moins que A ne soit multiple de 400. Tout cela dans une fonction.
Exercice 18:
Demander à l’utilisateur d’entrer trois longueurs a, b, c.
A l’aide de ces trois longueurs, déterminer s’il est possible de construire un triangle.
Déterminer ensuite si ce triangle est rectangle, isocèle, équilatéral ou quelconque.
Attention : un triangle rectangle peut être isocèle.
Créer et utiliser des fonctions.
6.1 - Elémentaires (Correction) ✔
Exercices : NSI - Première - Construction élémentaires
Capacités attendues : Mettre en évidence un corpus de constructions élémentaires. Commentaires : Séquences, affectation,conditionnelles, boucles bornées,boucles non bornées, appels de fonction.
De variables à conditions
Exercice 1 :
Ecrire un programme qui demande votre prénom et affiche "Bonjour Arthur", si la réponse est Arthur
prenom = input("Quel est votre prénom ? ")
if prenom == "Arthur":
print("Bonjour Arthur")Quel est votre prénom ?Arthur Bonjour Arthur
Exercice 2 :
Ecrire un programme qui demande 2 nombres entiers et affiche leur somme et leur produit avec une phrase du genre le produit de 3 et 5 est 15, leur somme est 8.
nombre1 = int(input("Entrez le premier nombre entier : "))
nombre2 = int(input("Entrez le deuxième nombre entier : "))
somme = nombre1 + nombre2
produit = nombre1 * nombre2
print("Le produit de ",nombre1," et ",nombre2," est ",produit,", et leur somme est", somme,".")Entrez le premier nombre entier: 2 Entrez le deuxième nombre entier: 3 Le produit de 2 et 3 est 6 , et leur somme est 5 .
Exercice 3 :
idem que l'exercice 2, mais avec des nombres décimaux.
nombre1 = float(input("Entrez le premier nombre décimal : "))
nombre2 = float(input("Entrez le deuxième nombre entier : "))
somme = nombre1 + nombre2
produit = nombre1 * nombre2
print("Le produit de ",nombre1," et ",nombre2," est ",produit,", et leur somme est", somme,".")Entrez le premier nombre décimal : 1.2 Entrez le deuxième nombre entier : 3.5 Le produit de 1.2 et 3.5 est 4.2 , et leur somme est 4.7 .
Exercice 4 :
Ecrire un programme qui demande deux nombres et qui dit "la somme est bien 100" ou "la somme ne fait pas 100".
nombre1, nombre2 = float(input("1er nombre: ")), float(input("2ème nombre: "))
if nombre1 + nombre2 == 100:
print("La somme est bien 100.")
else:
print("La somme ne fait pas 100.")1er nombre: 23 2ème nombre: 77 La somme est bien 100.
Exercice 5:
Ecrire un programme qui demande un prénom et qui dit "Bonjour Paul" ou "Bonjour, je croyais que c'était Paul".
prenom = input("Quel est votre prénom? ")
if prenom == "Paul":
print("Bonjour Paul !")
else:
print("Bonjour, je croyais que c'était Paul.")Quel est votre prénom? Paul Bonjour Paul !
Exercice 6:
Convertir une note scolaire N quelconque, entrée par l’utilisateur sous forme de points (par exemple 27 sur 85), en une note standardisée suivant le code ci-dessous : Note N Appréciation N >= 80 % A 80 % > N >= 60 % B 60 % > N >= 50 % C 50 % > N >= 40 % D N < 40 % E
score = float(input("Entrez votre note: "))
total = float(input("Entrez la note maximale: "))
pourcentage = (score / total) * 100
if pourcentage >= 80:
note = "A"
elif pourcentage >= 60:
note = "B"
elif pourcentage >= 50:
note = "C"
elif pourcentage >= 40:
note = "D"
else:
note = "E"
print("Votre appréciation est : ", note,".")Entrez votre note: 27 Entrez la note maximale: 85 Votre appréciation est : E .
Boucles bornées
Exercice 7:
Ecrire un programme qui affiche les carrés des entiers de 1 à 7 ?
for i in range(1, 8):
carre = i**2
print("Le carré de ",i," est ",carre,".")Le carré de 1 est 1 . Le carré de 2 est 4 . Le carré de 3 est 9 . Le carré de 4 est 16 . Le carré de 5 est 25 . Le carré de 6 est 36 . Le carré de 7 est 49 .
Exercice 8:
Écrire les nombres pairs jusqu'à 20.
for i in range(0, 21, 2):
print(i)0 2 4 6 8 10 12 14 16 18 20
Exercice 9:
Écrire un programme qui affiche les 20 premiers produits de la table de multiplication de 7.
for i in range(1, 21):
produit = 7 * i
print(f"7 x {i} = {produit}")7 x 1 = 7 7 x 2 = 14 7 x 3 = 21 7 x 4 = 28 7 x 5 = 35 7 x 6 = 42 7 x 7 = 49 7 x 8 = 56 7 x 9 = 63 7 x 10 = 70 7 x 11 = 77 7 x 12 = 84 7 x 13 = 91 7 x 14 = 98 7 x 15 = 105 7 x 16 = 112 7 x 17 = 119 7 x 18 = 126 7 x 19 = 133 7 x 20 = 140
Exercice 10:
Écrire un programme qui affiche une suite de 12 nombres dont chaque terme soit égal au double du terme précédent.
terme = 1 # Valeur initiale du premier terme
for i in range(12):
print(terme)
terme *= 21 2 4 8 16 32 64 128 256 512 1024 2048
Exercice 11:
Écrire un programme qui affiche les 20 premiers termes de la table de multiplication par 7, en signalant au passage (a l’aide d’une astérisque) ceux qui sont des multiples de 3.
for i in range(1, 21):
produit = 7 * i
if produit % 3 == 0:
print(f"7 x {i} = {produit} *") # Marqué avec une astérisque si c'est un multiple de 3
else:
print(f"7 x {i} = {produit}")7 x 1 = 7 7 x 2 = 14 7 x 3 = 21 * 7 x 4 = 28 7 x 5 = 35 7 x 6 = 42 * 7 x 7 = 49 7 x 8 = 56 7 x 9 = 63 * 7 x 10 = 70 7 x 11 = 77 7 x 12 = 84 * 7 x 13 = 91 7 x 14 = 98 7 x 15 = 105 * 7 x 16 = 112 7 x 17 = 119 7 x 18 = 126 * 7 x 19 = 133 7 x 20 = 140
Exercice 11:
Écrire un programme qui calcule les 50 premiers termes de la table de multiplication par 13, mais n’affiche que ceux qui sont des multiples de 7.
for i in range(1, 51):
produit = 13 * i
if produit % 7 == 0:
print(f"13 x {i} = {produit}")13 x 7 = 91 13 x 14 = 182 13 x 21 = 273 13 x 28 = 364 13 x 35 = 455 13 x 42 = 546 13 x 49 = 637
Exercice 12:
Ecrire un programme qui affiche la somme des premiers entiers jusqu'à 30.
somme = 0
for i in range(1, 31):
somme += i
print(f"La somme des premiers entiers jusqu'à 30 est {somme}.")La somme des premiers entiers jusqu'à 30 est 465.
Boucles non bornées
Exercice 13:
Ecrire un programme qui demande un prénom. Si ce prénom est Paul, le programme affiche "enfin c'est toi", sinon le programme redemande un nouveau prénom car ce n'est pas la personne qu'il attend.
prenom = ""
while prenom != "Paul":
prenom = input("Quel est votre prénom? ")
if prenom != "Paul":
print("Ce n'est pas la personne que j'attends.")
print("Enfin c'est toi!")Quel est votre prénom? William Ce n'est pas la personne que j'attends. Quel est votre prénom? Julie Ce n'est pas la personne que j'attends. Quel est votre prénom? Paul Enfin c'est toi!
Exercice 14:
Ecrire un programme qui additionne tous les nombres que vous entrez (tour à tour) et qui s'arrête lorsque vous tapez 0.
somme = 0
while True:
try:
nombre = float(input("Entrez un nombre (tapez 0 pour arrêter) : "))
if nombre == 0:
break
somme += nombre
except ValueError:
print("Ce n'est pas un nombre valide. Essayez encore.")
print(f"La somme des nombres entrés est {somme}.")Entrez un nombre (tapez 0 pour arrêter) : 1 Entrez un nombre (tapez 0 pour arrêter) : 2 Entrez un nombre (tapez 0 pour arrêter) : 5 Entrez un nombre (tapez 0 pour arrêter) : 0 La somme des nombres entrés est 8.0.
Exercice 15:
Ecrire un programme qui additionne tous les nombres que vous entrez (tour à tour) et qui s'arrête lorsque la somme dépasse 100.
somme = 0
while somme <= 100:
try:
nombre = float(input("Entrez un nombre: "))
somme += nombre
except ValueError:
print("Ce n'est pas un nombre valide. Essayez encore.")
print(f"La somme a dépassé 100 et est maintenant de {somme}.")Entrez un nombre: 10 Entrez un nombre: 77 Entrez un nombre: 23 La somme a dépassé 100 et est maintenant de 110.0.
Fonctions
Exercice 16:
Écrire une fonction qui calcule le volume d’un parallélépipède rectangle dont sont fournis au départ la largeur, la hauteur et la profondeur. Testez votre fonction.
def volume_parallelepipede(longueur, largeur, hauteur):
return longueur * largeur * hauteur
# Test de la fonction
longueur = float(input("Entrez la longueur du parallélépipède rectangle: "))
largeur = float(input("Entrez la largeur du parallélépipède rectangle: "))
hauteur = float(input("Entrez la hauteur du parallélépipède rectangle: "))
volume = volume_parallelepipede(longueur, largeur, hauteur)
print(f"Le volume du parallélépipède rectangle est: {volume} unités cube.")Entrez la longueur du parallélépipède rectangle: 2 Entrez la largeur du parallélépipède rectangle: 1 Entrez la hauteur du parallélépipède rectangle: 3 Le volume du parallélépipède rectangle est: 6.0 unités cube.
Exercice 17:
Déterminer si une année (dont le millésime est introduit par l’utilisateur) est bissextile ou non. Une année A est bissextile si A est divisible par 4. Elle ne l’est cependant pas si A est un multiple de 100, a moins que A ne soit multiple de 400. Tout cela dans une fonction.
def est_bissextile(annee):
if (annee % 4 == 0 and annee % 100 != 0) or annee % 400 == 0:
return True
return False
# Utilisation de la fonction
annee = int(input("Entrez un millésime: "))
if est_bissextile(annee):
print(f"L'année {annee} est bissextile.")
else:
print(f"L'année {annee} n'est pas bissextile.")Entrez un millésime: 2000 L'année 2000 est bissextile.
Exercice 18:
Demander à l’utilisateur d’entrer trois longueurs a, b, c.
A l’aide de ces trois longueurs, déterminer s’il est possible de construire un triangle.
Déterminer ensuite si ce triangle est rectangle, isocèle, équilatéral ou quelconque.
Attention : un triangle rectangle peut être isocèle.
Créer et utiliser des fonctions.
def peut_former_triangle(a, b, c):
return a + b > c and a + c > b and b + c > a
def est_rectangle(a, b, c):
# Nous trions les côtés pour que c soit le plus grand
a, b, c = sorted([a, b, c])
return a**2 + b**2 == c**2
def est_isocèle(a, b, c):
return a == b or a == c or b == c
def est_equilatéral(a, b, c):
return a == b == c
# Demander les longueurs à l'utilisateur
a = float(input("Entrez la longueur a: "))
b = float(input("Entrez la longueur b: "))
c = float(input("Entrez la longueur c: "))
if peut_former_triangle(a, b, c):
if est_equilatéral(a, b, c):
print("Le triangle est équilatéral.")
elif est_rectangle(a, b, c) and est_isocèle(a, b, c):
print("Le triangle est rectangle et isocèle.")
elif est_rectangle(a, b, c):
print("Le triangle est rectangle.")
elif est_isocèle(a, b, c):
print("Le triangle est isocèle.")
else:
print("Le triangle est quelconque.")
else:
print("Il n'est pas possible de former un triangle avec ces longueurs.")
Entrez la longueur a: 3 Entrez la longueur b: 4 Entrez la longueur c: 5 Le triangle est rectangle.
6.2 - Langages ✔
Langages et programmation
Diversité et unité des langages de programmation
Capacités Attendue :
Repérer, dans un nouveau langage de programmation, les traits communs et les traits particuliers à ce langage.
Commentaires :
Les manières dont un même programme simple s’écrit dans différents langages sont comparées.
Un langage de programmation est un ensemble de règles et de conventions utilisées pour écrire des programmes informatiques.
Il permet aux développeurs de spécifier des actions que l'ordinateur doit exécuter.
1. Diversité des Langages
Les langages de programmation sont diversifiés, et cette diversité est principalement due à des besoins spécifiques, des domaines d'application et des préférences des développeurs. Voici quelques exemples de langages de programmation populaires:
-
Python: Connu pour sa simplicité et sa lisibilité, Python est largement utilisé dans le développement web, la science des données et l'automatisation.
-
JavaScript: Utilisé pour le développement web, JavaScript est un langage de script côté client qui permet d'interagir avec les pages web.
-
C++: Un langage de programmation orienté objet utilisé pour le développement de logiciels système, de jeux et d'applications hautes performances.
-
Java: Connu pour sa portabilité, Java est utilisé pour le développement d'applications Android, de logiciels d'entreprise et de systèmes embarqués.
-
PHP est un langage de programmation très populaire pour le développement web côté serveur. Il est principalement utilisé pour créer des pages web dynamiques en générant du contenu HTML.
Au fil des années, de nouveaux langages ont vu le jour, chacun apportant ses propres innovations et approches. Parmi les dates clés:
1972: Apparition du langage Pascal.
1983: Introduction du langage C++, ainsi que de l'Objective-C.
1987: Création du langage Perl (PERL).
1990: Développement du langage HTML.
1991: Naissance de Python, un langage orienté objet et multiplateforme.
1994: Apparition de PHP, un langage utilisé pour les sites web côté serveur.
1995: Introduction de Java et de JavaScript, deux langages distincts. Java est multiplateforme, tandis que JavaScript s'exécute côté client sur les pages web.
2011: Émergence du langage Ruby, un langage orienté objet et multi-paradigme.
Certains langages sont compilés avant l'execution. Cela signifie qu'ils sont traduit avant d'être executés. Le C est un langage compilé en assembleur, une fois compilé, le programme est donc directement compris par la machine et est donc plus rapide. Le java est compilé en bytecode et ce bytecode est ensuite interprété gràce à une machine virtuelle (JVM) dépendante du système d'exploitation. Lors des procédures de compilation, un certains nombres d'erreurs sont détectées et signalés. Le programme doit être corrigé.
Python est classé dans les langages interprétés car il ne produit pas de fichier compilé contrairement à java. Un langage interprété est lu et converti en assembleur au fur et à mesure de son execution. Ce qui rend le programme plus lent et qui oblige parfois à re-compiler des parties déjà utilisées. Un programme interpréteur permet d’exécuter le code Python sur n’importe quel ordinateur. Les langages interprétés ont pour avantage de voir rapidement les résultats d’un changement dans le code. Python est toutefois plus complexe et est dans les faits Python compile en bytecode dans le fichier .py
2. Traits Communs et Traits Particuliers
Chaque langage de programmation a ses propres caractéristiques, mais il existe des concepts communs qui se retrouvent dans la plupart d'entre eux:
- Variables: Les variables sont utilisées pour stocker des données temporaires.
- Structures de Contrôle: Les structures de contrôle, telles que les boucles et les conditions, permettent de prendre des décisions dans un programme.
- Fonctions: Les fonctions sont des blocs de code réutilisables qui effectuent une tâche spécifique.
- Types de Données: Les langages de programmation ont différents types de données (entiers, chaînes de caractères, etc.) pour représenter différentes informations.
Cependant, chaque langage a également ses caractéristiques particulières. Par exemple, Python est connu pour son indentation significative, tandis que C++ offre un contrôle plus précis sur la mémoire.
Certains langage obligent la déclaration de variables avant leur utilisation. C'est le cas de Java, javascript, aseba. Il faut en plus de la déclaration de l'existance de la variable, parfois donner son type comme en java.
En php toutes les variables sont précédées d'un $
Pour reconnaitre le début d'un bloc crée par un if, for, while etc, Python utilise l'indentation, mais de nombreux langages utilisent les accolades de début et fin.
De nombreux langages signalent la fin d'une ligne de programme par un point virgule
Enfin les commandes ne sont pas les mêmes mais on retrouve tout de même les mêmes mots clés pour les commandes de base.
3. Comparaison de Programmes Simples
Pour illustrer la diversité des langages de programmation, nous pouvons examiner un programme simple dans différents langages. Ces exemples définissent une fonction nommée sommeDe1A100() qui calcule la somme des nombres de 1 à 100 et affiche le résultat.
Python :
def sommeDe1A100():
somme = 0
for i in range(1, 101):
somme += i
return somme
resultat = sommeDe1A100()
print("La somme des nombres de 1 à 100 est :", resultat)La somme des nombres de 1 à 100 est : 5050
JavaScript :
function sommeDe1A100() {
let somme = 0;
for (let i = 1; i <= 100; i++) {
somme += i;
}
return somme;
}
let resultat = sommeDe1A100();
console.log("La somme des nombres de 1 à 100 est :", resultat);php :
function sommeDe1A100() {
$somme = 0;
for ($i = 1; $i <= 100; $i++) {
$somme += $i;
}
return $somme;
}
$resultat = sommeDe1A100();
echo "La somme des nombres de 1 à 100 est : " . $resultat;
C++:
#include <iostream>
using namespace std;
int sommeDe1A100() {
int somme = 0;
for (int i = 1; i <= 100; i++) {
somme += i;
}
return somme;
}
int main() {
int resultat = sommeDe1A100();
cout << "La somme des nombres de 1 à 100 est : " << resultat << endl;
return 0;
}Java :
public class SommeDe1A100 {
public static int sommeDe1A100() {
int somme = 0;
for (int i = 1; i <= 100; i++) {
somme += i;
}
return somme;
}
public static void main(String[] args) {
int resultat = sommeDe1A100();
System.out.println("La somme des nombres de 1 à 100 est : " + resultat);
}
}6.3 - Spécification
Langages et programmation
Spécification
Capacités Attendue :
- Prototyper une fonction.
- Décrire les préconditions sur les arguments.
- Décrire des postconditions sur les résultats.
Commentaires :
Des assertions peuvent être utilisées pour garantir des préconditions ou des postconditions.
1. Spécification :
La spécification d'une fonction décrit ce que la fonction est censée faire sans dire comment elle le fait. Elle sert à définir le comportement attendu de la fonction.
Dans la pratique, la spécification est souvent écrite sous forme de documentation externe ou de commentaires dans le code, plutôt que d'être intégrée directement dans le programme. La spécification sert de guide pour les développeurs qui utiliseront ou modifieront la fonction à l'avenir.
def convertir_temperature(temperature: float, unite_origine: str, unite_cible: str) -> float:
"""
Convertit une température d'une unité à une autre.
Arguments:
- temperature (float): La valeur de la température à convertir.
- unite_origine (str): L'unité de la température d'origine. Les valeurs acceptables sont "Celsius", "Fahrenheit" et "Kelvin".
- unite_cible (str): L'unité dans laquelle la température doit être convertie. Les valeurs acceptables sont les mêmes que pour unite_origine.
Retour:
- float: La température convertie.
Erreurs/Exceptions:
- ValueError: Si unite_origine ou unite_cible n'est pas l'une des unités acceptables.
- ValueError: Si la conversion n'est pas possible (par exemple, une température en Kelvin inférieure à zéro).
"""
if unite_origine == "Celsius":
if unite_cible == "Fahrenheit":
return (temperature * 9/5) + 32
elif unite_cible == "Kelvin":
return temperature + 273.15
elif unite_origine == "Fahrenheit":
if unite_cible == "Celsius":
return (temperature - 32) * 5/9
elif unite_cible == "Kelvin":
return (temperature - 32) * 5/9 + 273.15
elif unite_origine == "Kelvin":
if unite_cible == "Celsius":
return temperature - 273.15
elif unite_cible == "Fahrenheit":
return (temperature - 273.15) * 9/5 + 32
else:
raise ValueError("Unité non reconnue")help(convertir_temperature)Help on function convertir_temperature in module __main__:
convertir_temperature(temperature: float, unite_origine: str, unite_cible: str) -> float
Convertit une température d'une unité à une autre.
Arguments:
- temperature (float): La valeur de la température à convertir.
- unite_origine (str): L'unité de la température d'origine. Les valeurs acceptables sont "Celsius", "Fahrenheit" et "Kelvin".
- unite_cible (str): L'unité dans laquelle la température doit être convertie. Les valeurs acceptables sont les mêmes que pour unite_origine.
Retour:
- float: La température convertie.
Erreurs/Exceptions:
- ValueError: Si unite_origine ou unite_cible n'est pas l'une des unités acceptables.
- ValueError: Si la conversion n'est pas possible (par exemple, une température en Kelvin inférieure à zéro).
convertir_temperature(20,"Celsius", "Fahrenheit")2. Le Prototypage :
Le prototypage d'une fonction se réfère à la définition de sa structure de base, c'est-à-dire la manière dont elle sera appelée, les arguments qu'elle acceptera et le type de données qu'elle renverra. C'est en quelque sorte la "signature" de la fonction.
Avantages du prototypage :
- Clarté: Il permet aux développeurs de comprendre rapidement comment utiliser une fonction sans avoir à plonger dans sa logique interne.
- Détection précoce des erreurs: En définissant les types d'arguments et les valeurs de retour, les erreurs peuvent être détectées tôt lors de la compilation ou de l'interprétation.
- Documentation: Le prototype sert de documentation intégrée au code, indiquant comment la fonction doit être utilisée.
Exemples :
def saluer(nom: str) -> str:
return f"Bonjour, {nom}!"
message = saluer("Alice")
print(message)Bonjour, Alice!
⚠
Dans def saluer(nom: str) -> str: , le -> str est juste un annotation.
Elle n'affecte pas la manière dont le code s'exécute
import math
def aire_cercle(rayon: float) -> float:
return math.pi * rayon * rayon
a = aire_cercle(5)
print(f"L'aire du cercle de rayon 5 est {a:.2f} .")L'aire du cercle de rayon 5 est 78.54 .
def inverser_mots(phrase: str) -> str:
mots = phrase.split()
mots_inverses = mots[::-1]
return ' '.join(mots_inverses)
phrase = "parfois simple , souvent compliqué"
phrase_inversee = inverser_mots(phrase)
print(phrase_inversee)compliqué souvent , simple Parfois
def diviser_et_reste(a: int, b: int) -> (int, int):
if b == 0:
raise ValueError("Le dénominateur ne peut pas être zéro.")
quotient = a // b
reste = a % b
return (quotient, reste)
quotient, reste = diviser_et_reste(10, 3)
print(f"Quotient: {quotient}, Reste: {reste}")
Quotient: 3, Reste: 1
def afficher_greeting(message: str, majuscule: bool = False):
if majuscule:
print(message.upper())
else:
print(message)
afficher_greeting("Bonjour tout le monde!")
afficher_greeting("Bonjour tout le monde!", True) Bonjour tout le monde! BONJOUR TOUT LE MONDE!
3. Préconditions :
Les préconditions sont des conditions ou des exigences qui doivent être remplies avant qu'une fonction ne soit appelée. Elles définissent ce qui est attendu des arguments ou de l'état du programme avant l'exécution de la fonction. Si les préconditions ne sont pas satisfaites, la fonction peut ne pas se comporter comme prévu, produire des résultats incorrects ou même provoquer des erreurs.
Exemples :
def racine_carree(x: float) -> float:
assert x >= 0, "L'argument doit être positif ou nul"
return x ** 0.5
racine_carree(-1)assert est utilisé pour signaler des erreurs en Python :
- Vérifie si quelque chose est vrai.
- Si ce n'est pas vrai, le programme s'arrête et montre une erreur.
- Utilisé surtout pendant le développement pour détecter des bugs.
En résumé, les préconditions sont essentielles pour garantir que les fonctions fonctionnent correctement et produisent les résultats attendus. Elles définissent les "règles du jeu" pour l'utilisation d'une fonction et aident à prévenir des erreurs courantes.
4. Postconditions :
Les postconditions décrivent ce qui est garanti après l'exécution de la fonction, c'est-à-dire l'état dans lequel la fonction laissera le système ou les garanties sur les valeurs retournées. Par exemple, après avoir trié une liste, une postcondition pourrait être que la liste est en ordre croissant.
Exemple :
def tri_liste(liste: list) -> list:
liste_triee = sorted(liste)
# Vérification des postconditions
assert len(liste) == len(liste_triee), "Les listes doivent avoir la même taille"
for item in liste:
assert item in liste_triee, f"{item} doit être dans la liste triée"
for i in range(len(liste_triee) - 1):
assert liste_triee[i] <= liste_triee[i+1], "La liste n'est pas en ordre croissant"
return liste_triee
liste_a_trier = [23, 1, 45, 6, 12, 89, 4, 28]
tri_liste(liste_a_trier)En résumé, la spécification et le prototypage aident à comprendre et à définir le comportement attendu d'une fonction. Les préconditions, postconditions et assertions aident à s'assurer que la fonction fonctionne comme prévu.
6.4 - Mise au point de programmes ✔
Langages et programmation
Mise au point de programmes
Capacités Attendue :
Utiliser des jeux de tests.
Commentaires :
- L’importance de la qualité et du nombre des tests est mise en évidence.
- Le succès d’un jeu de tests ne garantit pas la correction d’un programme.
La mise au point d'un programme fait référence à l'ensemble des activités visant à déterminer la présence de défauts dans un programme et à les corriger. L'une des méthodes les plus courantes pour cela est l'utilisation de jeux de tests.
Un jeu de tests est un ensemble spécifique de données d'entrée préparées pour tester la validité d'un programme. Il est conçu pour tester si un programme fonctionne comme prévu, identifie les erreurs et les problèmes potentiels.
Exemple 1 : Fonction d'Addition
def addition(a, b):
return a + bJeu de tests pour cette fonction :
assert addition(1, 1) == 2
assert addition(2, 3) == 5
assert addition(-1, 1) == 0Exemple 2 :
def trouver_max(liste):
return max(liste)assert trouver_max([1, 2, 3, 4, 5]) == 5
assert trouver_max([-5, -4, -3, -2, -1]) == -1Exemple 3 : inverse une chaîne de caractères
def inverser(chaine):
return chaine[::-1]assert inverser("abc") == "cba"
assert inverser("Python") == "nohtyP"Le Succès d'un Jeu de Tests ne Garantit pas la Correction d'un Programme.
Pour anticiper les erreurs, il est essentiel de créer des jeux de tests complets qui couvrent divers scénarios d'utilisation du programme.
Retour à l'exemple 1 : Fonction d'Addition
assert addition(0.1, 0.2) == 0.3Exemple 4 : Division
def diviser(a, b):
return a / bassert diviser(4, 2) == 2
assert diviser(9, 3) == 3Mais si vous n'avez pas de test pour la division par zéro, vous pourriez manquer une erreur potentielle.
diviser(1, 0)Exemple 5 : Multiplier un entier par un décimal
def multiplier(a, b):
"""
Cette fonction multiplie deux nombres.
:param a: Premier nombre entier
:param b: Deuxième nombre entier ou décimal
:return: Le produit de a et b
"""
assert isinstance(a, int), "a doit être un nombre entier"
assert isinstance(b, (int, float)), "b doit être un nombre entier ou décimal"
return a * b
# Jeu de tests
assert multiplier(1, 2) == 2
assert multiplier(-1, 1) == -1
assert multiplier(0.1, 0) == 0
6.5 - Bibliothèques ✔
Langages et programmation
Utilisation de bibliothèques
Capacités Attendue :
Utiliser la documentation d’une bibliothèque.
Commentaires :
Aucune connaissance exhaustive d’une bibliothèque particulière n’est exigible.
Une bibliothèque en programmation est une collection de fonctions et de méthodes prédéfinies que vous pouvez utiliser pour effectuer des tâches spécifiques, évitant ainsi d'avoir à écrire le code à partir de zéro.
1. Comment utiliser une bibliothèque - Exemple avec la bibliothèque math
- Installation : La première étape consiste à installer la bibliothèque. Par exemple, en Python, vous pouvez utiliser pip pour installer des bibliothèques.
pip install math- Importation: Une fois installée, la bibliothèque doit être importée dans votre code.
import math- Utilisation: Après l'importation, vous pouvez utiliser les fonctions et les méthodes fournies par la bibliothèque.
math.sqrt(2)2. Les modules Python
Pour vraiment maîtriser l'utilisation des bibliothèques en Python, il est essentiel de savoir comment accéder aux informations sur ce qu'ils contiennent et comment ils fonctionnent.
Liste des fonctions et classes d'un module:
Après avoir importé une bibliothèque, vous pouvez utiliser la fonction dir() pour lister tous ses attributs, fonctions, et classes:
import math
print(dir(math))['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'cbrt', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'exp2', 'expm1', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
Cela vous donne une liste de toutes les fonctions et constantes disponibles dans le module math.
Utiliser l'aide:
La fonction help() est intégrée à Python et permet d'afficher la documentation d'une fonction, classe ou module:
help(math.sqrt)Help on built-in function sqrt in module math:
sqrt(x, /)
Return the square root of x.
Cela affiche une explication sur la fonction sqrt() du module math.
Accéder à la documentation (docstrings):
La plupart des fonctions, classes, et modules en Python contiennent des chaînes de documentation, ou docstrings, qui fournissent une explication concise de leur utilité et de leur utilisation. Vous pouvez y accéder en utilisant l'attribut doc:
print(math.cos.__doc__)Return the cosine of x (measured in radians).
Cela affichera la docstring pour la fonction cos().
Lorsque vous travaillez avec des packages tiers (ceux que vous installez via pip, par exemple), la documentation officielle ou la page GitHub du package est souvent le meilleur endroit pour trouver des informations. Les grands packages tels que NumPy, pandas ou Flask ont des documentations complètes disponibles en ligne.
Des environnements de développement intégrés (IDE) comme PyCharm, Visual Studio Code (avec l'extension Python), et autres offrent souvent des fonctionnalités d'introspection qui permettent de voir rapidement la documentation ou la signature d'une fonction en passant simplement la souris dessus ou en appuyant sur une combinaison de touches.
Si vous avez besoin d'une compréhension plus profonde de la manière dont un module ou une fonction fonctionne, et que la documentation ne suffit pas, vous pouvez souvent consulter directement le code source. Pour les modules de la bibliothèque standard ou les packages installés via pip, vous pouvez généralement trouver le code source sur GitHub ou d'autres plateformes de gestion de code source.
3. Les déclarations import en Python
Les déclarations import en Python sont utilisées pour accéder aux fonctions, classes, variables et autres éléments d'un module. Je vais décomposer chaque forme d'importation.
3.1 import
La déclaration import est utilisée pour importer un module entier.
Après avoir exécuté l'instruction ci-dessous, vous pouvez accéder à toutes les fonctions et variables définies dans le module math en utilisant la notation pointée. Par exemple, math.sqrt(2) renverrait 1.4142135623730951.
import math
math.sqrt(2)3.2 from ... import ...
La déclaration from ... import ... est utilisée pour importer des éléments spécifiques (comme des fonctions, des classes ou des variables) d'un module.
Avec cette forme d'importation, vous n'avez plus besoin d'utiliser la notation pointée pour accéder à la fonction sqrt. Vous pouvez simplement écrire sqrt(2).
from math import sqrt
sqrt(2)3.3 from ... import *
La déclaration from ... import * importe tous les éléments d'un module directement dans l'espace de noms courant. Cela signifie que vous n'aurez pas à utiliser la notation pointée pour accéder à ces éléments. Après cette instruction, vous pouvez directement utiliser des fonctions comme sqrt, sin, cos, etc., sans préfixe.
from math import *
sqrt(2)⚠ : Bien que cette méthode d'importation puisse sembler pratique, elle est généralement déconseillée car elle peut rendre le code moins lisible (il devient plus difficile de déterminer d'où proviennent certaines fonctions ou variables) et peut causer des conflits si deux modules importés ont des fonctions ou des variables avec le même nom.
3.4 from module_name import element_name as alias
Vous pouvez également attribuer un alias à des éléments spécifiques lors de leur importation.
from math import sqrt as racine_carree
racine_carree(2)3.5 import module_name as alias
Lorsque vous importez un module entier, vous pouvez lui attribuer un alias pour rendre votre code plus concis ou pour éviter des conflits de noms.
import numpy
A = numpy.array([[1, 2], [3, 4]])
print(A)[[1 2] [3 4]]
import numpy as np
A = np.array([[1, 2], [3, 4]])
print(A)[[1 2] [3 4]]
7.1 - Parcours séquentiel ✔
Algorithmique
Parcours séquentiel d’un tableau
Capacités attendues :
- Écrire un algorithme de recherche d’une occurrence sur des valeurs de type quelconque.
- Écrire un algorithme de recherche d’un extremum, de calcul d’une moyenne.
Commentaires : On montre que le coût est linéaire.
Recherche d'une Occurrence
Pour rechercher une valeur dans un tableau, vous pouvez utiliser une boucle for qui passe en revue chaque élément :
def recherche_occurrence(tableau, valeur):
for i in range(len(tableau)):
if tableau[i] == valeur:
return i # Retourne l'index si la valeur est trouvée
return -1 # Retourne -1 si la valeur n'est pas trouvée
print("Exemple d'utilisation 1")
tableau = [1, 2, 3, 4, 5]
index = recherche_occurrence(tableau, 3)
print("Index :", index)
print("Exemple d'utilisation 2")
tableau = ['Paul', 'Pierre', 'Jacque', 'Louis', 'Marc']
index = recherche_occurrence(tableau, 'Louis')
print("Index :", index)Exemple d'utilisation 1 Index : 2 Exemple d'utilisation 2 Index : 3
Recherche d'un Extremum
def recherche_extremum(tableau):
minimum = tableau[0]
maximum = tableau[0]
for element in tableau:
if element < minimum:
minimum = element
if element > maximum:
maximum = element
return minimum, maximum
# Exemple d'utilisation
tableau = [x**3 -3*x**2 + 2 for x in range(-1,11,1)]
min_val, max_val = recherche_extremum(tableau)
print("Minimum:", min_val)
print("Maximum:", max_val)
Minimum: -2 Maximum: 702
Calcul de la moyenne simple
def calcul_moyenne(tableau):
somme = 0
for element in tableau:
somme += element
moyenne = somme / len(tableau)
return moyenne
# Exemple d'utilisation
tableau = [11, 20, 13, 14, 15]
moyenne = calcul_moyenne(tableau)
print("Moyenne :", moyenne)
Moyenne : 14.6
Coût Linéaire
La notation O(f(n)) est une généralisation de la notion de complexité d'un algorithme, où f(n) est une fonction positive de $n$, la taille de l'entrée de l'algorithme. La notation O(f(n))indique que la croissance du temps d'exécution de l'algorithme est "limitée supérieurement" par une constante multiple de f(n) lorsque n tend vers l'infini.
En d'autres termes, si un algorithme a une complexité O(f(n)), alors le temps d'exécution T(n) est au plus une constante C multipliée par f(n) pour de grandes valeurs de n:
$T(n)≤C×f(n)$ pour n suffisamment grand et une constante C.
Cela vous donne une "limite supérieure" sur le temps d'exécution de l'algorithme, ce qui vous permet de comprendre comment l'efficacité de l'algorithme change à mesure que la taille de l'entrée nn augmente.
Par exemple, si un algorithme a une complexité O($n^2$), cela signifie qu'en pire cas, le temps d'exécution augmentera quadratiquement en fonction de la taille de l'entrée. Cela ne vous donne pas le temps d'exécution exact, mais cela vous donne une idée de la manière dont le temps d'exécution évoluera lorsque la taille de l'entrée augmentera.
Exemples : Voici quelques exemples courants :
-
O(1) : Constant. Le temps d'exécution de l'algorithme est indépendant de la taille de l'entrée.
-
O(logn) : Logarithmique. Le temps d'exécution augmente logarithmiquement à mesure que la taille de l'entrée augmente. Un exemple est l'algorithme de recherche binaire.
-
O(n) : Linéaire. Le temps d'exécution augmente linéairement à mesure que la taille de l'entrée augmente. Les boucles simples qui parcourent un ensemble d'éléments ont souvent un temps O(n)O(n).
-
O(nlogn) : Linéarithmique. C'est souvent le cas pour des algorithmes qui divisent la donnée en sous-parties, comme le tri fusion (merge sort).
-
O($n2$), O(^$n3$), O($n^k$): Polynomial. Le temps d'exécution augmente selon une puissance de la taille de l'entrée. Les boucles imbriquées sur l'ensemble des données entrent souvent dans cette catégorie.
-
O($2^n$) : Exponentiel. Le temps d'exécution double avec chaque élément supplémentaire dans l'entrée. Ces algorithmes peuvent devenir très lents très rapidement.
-
O(n!): Factoriel. Le temps d'exécution augmente de manière factorielle, ce qui est encore pire que exponentiel. Un exemple est l'algorithme du voyageur de commerce via une approche "brute force".
Les algorithmes de Recherche d'une Occurrence, de Recherche d'un Extremum, de Calcul de la moyenne simple ont un coût O(n), où n est la taille du tableau. Cela signifie que le temps d'exécution augmente de manière linéaire avec le nombre d'éléments dans le tableau.
Démonstration :
Pour la recherche d'une Occurrence, nous parcourons le tableau élément par élément pour trouver une valeur donnée. Dans le pire des cas, nous devrons parcourir tout le tableau, ce qui donne un temps d'exécution linéaire en fonction de la taille du tableau n.
Pour trouver le minimum ou le maximum, nous devons examiner chaque élément du tableau une fois. Le temps d'exécution est donc proportionnel à n.
Pour calculer la moyenne, nous additionnons tous les éléments puis divisons par le nombre total d'éléments. Encore une fois, nous devons parcourir tout le tableau, ce qui donne un temps d'exécution proportionnel à nn. Raisonnement Général
Chacun de ces algorithmes consiste en une boucle unique qui parcourt une seule fois chacun des n éléments du tableau au plus.
7.2 - Tri par insertion, par sélection ✔
Algorithmique
Tris par insertion, par sélection
Capacités attendues :
- Écrire un algorithme de tri.
- Décrire un invariant de boucle qui prouve la correction des tris par insertion, par sélection.
Commentaires :
- La terminaison de ces algorithmes est à justifier.
- On montre que leur coût est quadratique dans le pire cas.
Tri par insertion
lwh. Merci!Autre vidéo
L'idée principale du tri par insertion est de construire progressivement une sous-séquence triée au début du tableau. À chaque étape, on prend un élément de la partie non triée et on l'insère à sa place appropriée dans la partie triée.
Début : Au départ, seul le premier élément est considéré comme trié.
Processus :
- Sélectionnez l'élément suivant : Commencez par le deuxième élément, car le premier est déjà considéré comme trié.
- Trouvez la position correcte : Comparez cet élément avec ceux de la partie triée (à gauche de l'élément) et déplacez tous les éléments qui sont plus grands d'une position vers la droite. Cela crée un espace où l'élément sélectionné peut être inséré.
- Insérez l'élément : Placez l'élément à sa position correcte dans la partie triée.
- Répétez : Répétez ces étapes pour chaque élément jusqu'à ce que vous atteigniez la fin du tableau.
Fin : Le processus se termine lorsque tous les éléments ont été insérés dans la partie triée, ce qui signifie que le tableau est entièrement trié.
Exemple :
Prenons le tableau [4, 3, 5, 1] comme exemple.
Étape 1 : Le tableau commence avec [4 | 3, 5, 1]. 4 est considéré comme trié.
Étape 2 : Insérez 3. Le tableau devient [3, 4 | 5, 1].
Étape 3 : Insérez 5. Le tableau reste [3, 4, 5 | 1], car 5 est déjà plus grand que 4.
Étape 4 : Insérez 1. Le tableau devient [1, 3, 4, 5].def tri_insertion(tab):
n = len(tab)
for i in range(1, n):
valeur_insertion = tab[i]
j = i
while j > 0 and valeur_insertion < tab[j-1]:
tab[j] = tab[j-1]
j = j - 1
tab[j] = valeur_insertion
return tab
# Exemple d'utilisation
tab = [4, 3, 5, 1]
print("Tableau trié:",tri_insertion(tab) )Tableau trié: [1, 3, 4, 5]
Invariant de boucle :
À la fin de chaque itération de la boucle externe, les éléments dans le sous-tableau tableau[0,...,i-1] sont triés.
Terminaison :
Le tri par insertion termine car la boucle externe itère de 1 à n, ce qui est une séquence finie.
De plus, la boucle interne se termine dès que j devient négatif ou dès que tableau[j] <= clé.
Tri par sélection
lwh. Merci!Autre vidéo
Le tri par sélection est une méthode de tri qui divise le tableau en deux parties : une partie triée et une partie non triée.
À chaque étape, il trouve le plus petit élément de la partie non triée et l'échange avec le premier élément non trié.
Début : Considérez le tableau entier comme non trié.
Processus :
- Recherchez le plus petit élément : Trouvez le plus petit élément dans la partie non triée du tableau.
- Échangez-le avec le premier élément non trié : Échangez ce plus petit élément trouvé avec l'élément situé au début de la partie non triée.
- Considérez cet élément comme trié : Déplacez la frontière entre la partie triée et la partie non triée d'une position vers la droite.
- Répétez : Répétez ces étapes pour chaque élément dans la partie non triée du tableau.
Fin : Le processus se termine lorsque la partie non triée du tableau est vide, ce qui signifie que le tableau est entièrement trié.
Exemple :
Considérons le tableau [4, 3, 5, 1].
Étape 1 : Le plus petit élément dans la partie non triée [4, 3, 5, 1] est 1.
Échangez 1 avec 4.
Le tableau devient [1 | 3, 5, 4].
Étape 2 : Le plus petit élément dans la partie non triée [3, 5, 4] est 3.
Il est déjà en première position, donc pas d'échange nécessaire.
Le tableau reste [1, 3 | 5, 4].
Étape 3 : Le plus petit élément dans [5, 4] est 4.
Échangez 4 avec 5.
Le tableau devient [1, 3, 4 | 5].
Étape 4 : 5 est le seul élément restant dans la partie non triée.
Il est déjà en position correcte.Le tableau final est [1, 3, 4, 5].
def tri_selection(arr):
for i in range(len(arr)):
min_idx = i
for j in range(i+1, len(arr)):
if arr[min_idx] > arr[j]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
# Exemple d'utilisation
arr = [12, 11, 13, 5, 6]
tri_selection(arr)
print("Tableau trié:", arr)Tableau trié: [5, 6, 11, 12, 13]
Invariant de boucle :
À la fin de chaque itération de la boucle externe, les éléments dans le sous-tableau tableau[0,...,i] sont les i+1 plus petits éléments du tableau, et ils sont triés.
Terminaison :
Le tri par sélection termine car la boucle externe itère de 0 à len(arr)-1, ce qui est une séquence finie. La boucle interne est également finie, car elle itère de i+1 à len(arr)-1.
Coût des lgorithmes de tris par insertion, par sélection
Les algorithmes de tris par insertion, par sélection ont un coût O($n^2$), où $n$ est la taille du tableau.
Cela signifie que le temps d'exécution augmente de manière quadratrique avec le nombre d'éléments dans le tableau.
Démonstration :
Comme chaque boucle interne peut prendre jusqu'à $n$ itérations et il y a $n$ boucles externes, cela donne un total de $n×n=n^2$ opérations dans le pire cas.
7.3 - k plus proches voisins ✔
Algorithmique
Algorithme des k plus proches voisins
Capacités attendues :
Écrire un algorithme qui prédit la classe d’un élément en fonction de la classe majoritaire de ses k plus proches voisins.
Commentaires :
Il s’agit d’un exemple d’algorithme d’apprentissage.
L'idée principale derrière l'algorithme k-NN (k Nearest Neighbors) est qu'un élément peut être classifié en fonction des éléments qui lui sont le plus proches dans l'espace des caractéristiques. Ainsi, pour prédire la classe d'un élément donné, on regarde les k éléments les plus proches de cet élément (où "k" est un nombre entier positif), et on attribue à cet élément la classe majoritaire parmi ces voisins.
Étapes :
- Choisissez la valeur de k (nombre de voisins à considérer). Pour un élément donné que vous souhaitez classer :
- Calculez la distance entre cet élément et tous les autres éléments de l'ensemble d'apprentissage.
- Sélectionnez les k éléments ayant la plus faible distance par rapport à l'élément donné.
- Comptez le nombre d'occurrences de chaque classe parmi ces k voisins.
- Attribuez à l'élément la classe qui est la plus fréquente parmi ces k voisins.
Distances couramment utilisées :
- Distance euclidienne
- Distance de Manhattan
- Distance de Minkowski
- Et d'autres...
Inconvénients :
- Coûteux en temps de calcul, surtout lorsque la taille de l'ensemble de données est grande.
- Sensible aux variables non pertinentes.
- La performance peut être affectée par la valeur de k choisie.
Exemple : Classification de fruits en fonction de leur poids et de leur texture
Contexte : Supposons que nous ayons un ensemble de données de fruits, principalement des pommes et des oranges. Nous voulons classer un fruit inconnu en fonction de son poids (en grammes) et de sa texture (mesurée sur une échelle de 1 à 10, où 1 est très rugueux et 10 est très lisse).
Ensemble d'apprentissage :
- Pomme : 150g, texture 4
- Pomme : 170g, texture 5
- Orange : 160g, texture 7
- Orange : 140g, texture 8
- Pomme : 130g, texture 3
- Orange : 155g, texture 9
Fruit à classifier : ? : 145g, texture 6
Résultats :
- Distance entre le fruit inconnu et la 1ère pomme = $\sqrt{(150-145)^2+(4-6)^2} = \sqrt{29} \approx 5.39$
- Distance entre le fruit inconnu et la 2ème pomme $\approx$ 25.02
- Distance entre le fruit inconnu et la 1ère orange $\approx$ 15.03
- Distance entre le fruit inconnu et la 2ème orange $\approx$ 5.39
- Distance entre le fruit inconnu et la 3ème pomme $\approx$ 15.3
- Distance entre le fruit inconnu et la 2ème orange $\approx$ 10.44
Les 3 plus proches voisins sont donc la 2ème orange, la 1ère orange et la 2ème pomme. Parmi eux, nous avons 2 oranges et 1 pomme.
Conclusion : La classe majoritaire parmi les 3 plus proches voisins est "Orange". Par conséquent, nous classifions le fruit inconnu comme une "Orange".
Exercice de Classification : Détection du Diabète
Contexte : Le diabète est une maladie caractérisée par une augmentation chronique du taux de glucose dans le sang. Un test courant pour diagnostiquer le diabète est le test de glycémie à jeun. Un résultat supérieur à 126 mg/dL est généralement considéré comme indicatif du diabète.
Données : Vous disposez des résultats de glycémie à jeun pour un groupe de patients :
Patient A: 130 mg/dL
Patient B: 110 mg/dL
Patient C: 140 mg/dL
Patient D: 125 mg/dL
Patient E: 135 mg/dLQuestions :
-
En utilisant la valeur seuil de 126 mg/dL, classez chaque patient comme "Diabétique" ou "Non diabétique".
-
Si vous deviez utiliser l'algorithme des k plus proches voisins (k-NN) avec k=3 pour déterminer la classification d'un nouveau patient avec une glycémie de 128 mg/dL, comment le classeriez-vous ? (Considérez que la distance est simplement la différence absolue entre les valeurs de glycémie.)
-
Quels sont les avantages et les inconvénients de l'utilisation d'une valeur seuil fixe par rapport à l'utilisation de l'algorithme k-NN pour ce type de classification ?
Réponse :
- En utilisant la valeur seuil de 126 mg/dL, classez chaque patient comme "Diabétique" ou "Non diabétique".
- Patient A: 130 mg/dL -> Diabétique
- Patient B: 110 mg/dL -> Non diabétique
- Patient C: 140 mg/dL -> Diabétique
- Patient D: 125 mg/dL -> Non diabétique
- Patient E: 135 mg/dL -> Diabétique
- Si vous deviez utiliser l'algorithme des k plus proches voisins (k-NN) avec k=3k=3 pour déterminer la classification d'un nouveau patient avec une glycémie de 128 mg/dL, comment le classeriez-vous ?
Pour cela, nous allons calculer la distance (différence absolue) entre le nouveau patient et chaque patient existant :
- Distance avec A: |130 - 128| = 2
- Distance avec B: |110 - 128| = 18
- Distance avec C: |140 - 128| = 12
- Distance avec D: |125 - 128| = 3
- Distance avec E: |135 - 128| = 7
Les trois plus petites distances sont pour les patients A, D et E.
Parmi ces trois patients, deux sont diabétiques (A et E) et un est non diabétique (D). Ainsi, la majorité est "Diabétique".
donc Le nouveau patient serait classé comme "Diabétique" en utilisant k-NN avec k=3.
- Quels sont les avantages et les inconvénients de l'utilisation d'une valeur seuil fixe par rapport à l'utilisation de l'algorithme k-NN pour ce type de classification ?
Avantages de la valeur seuil :
Simple à comprendre et à implémenter.
Pas besoin de stocker tout l'ensemble de données pour les nouvelles classifications.
Rapide pour classer de nouvelles données.Inconvénients de la valeur seuil :
Peut ne pas être précis si la limite n'est pas clairement définie.
Ne prend pas en compte la distribution globale des données.Avantages de k-NN :
Prend en compte la distribution globale des données.
Flexible et peut être adapté en changeant la valeur de k.
Pas besoin d'un modèle formel, utilise directement les données pour la classification.Inconvénients de k-NN :
Nécessite de stocker tout l'ensemble de données, ce qui peut être coûteux en termes de mémoire.
Plus lent pour classer de nouvelles données car il faut calculer la distance avec chaque point de l'ensemble de données.import math
# Données d'entraînement
ensemble_apprentissage = [
{"fruit": "Pomme", "poids": 150, "texture": 4},
{"fruit": "Pomme", "poids": 170, "texture": 5},
{"fruit": "Orange", "poids": 160, "texture": 7},
{"fruit": "Orange", "poids": 140, "texture": 8},
{"fruit": "Pomme", "poids": 130, "texture": 3},
{"fruit": "Orange", "poids": 155, "texture": 9},
]
# Fruit à classer
fruit_inconnu = {"poids": 145, "texture": 6}
def distance_euclidienne(a, b):
return math.sqrt((a["poids"] - b["poids"])**2 + (a["texture"] - b["texture"])**2)
def kNN(ensemble, point, k):
distances = []
for élément in ensemble:
d = distance_euclidienne(élément, point)
distances.append((d, élément["fruit"]))
# Tri simplifié des distances
distances.sort()
print(distances)
# Sélection des k plus proches voisins
k_voisins = [item[1] for item in distances[:k]]
print(k_voisins)
# Détermination de la classe majoritaire sans Counter
classes = {}
for v in k_voisins:
if v in classes:
classes[v] += 1
else:
classes[v] = 1
print(classes)
# Détermination de la classe majoritaire
classe_majoritaire = None
max_count = 0
for fruit, count in classes.items():
if count > max_count:
max_count = count
classe_majoritaire = fruit
return classe_majoritaire
# Test
k = 3
classe_predite = kNN(ensemble_apprentissage, fruit_inconnu, k)
print(f"Le fruit inconnu est classé comme une {classe_predite}.")
[(5.385164807134504, 'Orange'), (5.385164807134504, 'Pomme'), (10.44030650891055, 'Orange'), (15.033296378372908, 'Orange'), (15.297058540778355, 'Pomme'), (25.019992006393608, 'Pomme')]
['Orange', 'Pomme', 'Orange']
{'Orange': 2, 'Pomme': 1}
Le fruit inconnu est classé comme une Orange.
7.4 - Dichotomique tableau trié ✔
Algorithmique
Recherche dichotomique dans un tableau trié
Capacités Attendue :
Montrer la terminaison de la recherche dichotomique à l’aide d’un variant de boucle.
Commentaires :
- Des assertions peuvent être utilisées.
- La preuve de la correction peut être présentée par le professeur.
1. Méthode naïve : recherche par balayage
Le but est de rechercher l'indice d'un élément spécifique dans un tableau trié.
Considérons donc le tableau suivante : [2, 3, 6, 7, 11, 14, 18, 19, 24]
def trouve(lst,val) :
for k in range(len(lst)) :
if lst[k] == val:
return k
return "non trouvé"
lst = [2, 3, 6, 7, 11, 14, 18, 19, 24]
val = 19
trouve(lst,val)Remarques :
- Dans le cas d'une recherche naïve, le nombre maximal d'opérations nécessaires est proportionnel à la taille de la liste à étudier. Si on appelle n la longueur de la liste, on dit que cet algorithme est d'ordre n , ou linéaire, ou en O(n).
- La méthode naïve n'utilise pas le fait que la liste est triée, on aurait pu aussi bien l'utiliser sur une liste non triée.
2. Recherche dichotomique
Comme dans le jeu pour faire deviner un nombre a quelqu'un, la meilleure stratégie est de couper en deux à chaque fois l'intervalle d'étude. C'est ce que l'on appelle une rechercher dichotomique.
Explication :
Recherdre de 19
- [2, 3, 6, 7, 11, 14, 18, 19, 24] et 11 < 19
- [14, 18, 19, 24] et 18 < 19
- [19, 24]
- [19]
Méthode : Recherche dichotomique
- on se place au milieu de la liste.
- on regarde si la valeur sur laquelle on est placée est inférieure ou supérieure à la valeur cherchée.
- on ne considère maintenant que la bonne moitié de la liste qui nous intéresse.
- on continue jusqu'à trouver la valeur cherchée (ou pas)
def recherche_dichotomique(lst,val):
indice_debut = 0
indice_fin = len(lst) - 1
while indice_debut <= indice_fin:
milieu = (indice_debut + indice_fin) // 2
if lst[milieu] == val:
return milieu # L'élément a été trouvé
elif lst[milieu] < val:
indice_debut = milieu + 1 # Recherche dans la moitié droite
else:
indice_fin = milieu - 1 # Recherche dans la moitié gauche
return None # L'élément n'a pas été trouvé
lst = [2, 3, 6, 7, 11, 14, 18, 19, 24]
val = 19
indice = recherche_dichotomique(lst,val)
print(indice)
assert lst[indice] == val
assert lst[0] <= lst[indice] <= lst[-1]
7
Terminaison :
A chaque étape : indice_debut = milieu + 1 ou indice_fin = milieu - 1 ou l'indice est trouvé. Donc où l'indince est trouvé, et le programme s'arrête ou il va arriver à un moment indice_fin > indice_debut, et le programme s'arrête aussi en sortant de la boule while.
Complexité :
Définissons maintenant le nombre d'itérations nécessaires pour trouver l'élément comme étant T(n), où n est la taille du tableau initial.
- Au premier tour de boucle, la taille du tableau est inférieur à $\frac{n}{2}$.
- Au deuxième tour de boucle, la taille du tableau est inférieur à $\frac{n}{4}$.
- Au troisième tour de boucle, la taille du tableau est inférieur à $\frac{n}{8}$.
- Et ainsi de suite...
Donc la taille du tableau est inférieur à chaque itération à $\frac{n}{2^k}$, où $k$ est le nombre d'itérations.
L'algorithme se termine lorsque la taille du tableau est de 1, c'est-à-dire $\frac{n}{2^k}\leq1$.
$\frac{n}{2^k}\leq 1 <=> n \leq 2^k <=> log_2(n) \leq k$
Donc, le nombre maximum d'itérations, T(n), est limité par $log_2(n) + 1$.
Formellement, on peut écrire : $T(n) \leq log_2(n) +1$.
Donc la complexité de l'algorithme de Recherche dichotomique est $O(log_2(n))$.
On dit que la recherche dichotomique a avec une complexité logarithmique.
Cette complexité est bien meilleure qu'une complexité linéaire. Ce qui en fait un algorithme très efficace.
Remarque :
Il ne faut toutefois pas oublier que la méthode dichotomique, bien plus rapide, nécessite que la liste ait été auparavant triée.
Ce qui rajoute du temps de calcul ! (Voir tri par insertion ou tri par sélection )
7.5 - Algorithmes gloutons ✔
Algorithmique
Algorithmes gloutons
Capacités attendues :
- Résoudre un problème grâce à un algorithme glouton.
Commentaires :
- Exemples : problèmes du sac à dos ou du rendu de monnaie.
- Les algorithmes gloutons constituent une méthode algorithmique parmi d’autres qui seront vues en terminale.
Un algorithme glouton est une méthode algorithmique qui suit le principe de prendre la meilleure solution locale à chaque étape dans l'espoir de trouver une solution globale optimale. En d'autres termes, à chaque étape du processus, l'algorithme fait un choix qui semble être le meilleur à ce moment-là, sans considérer les conséquences futures de ce choix. Ce type d'algorithme vise à résoudre un problème en prenant la décision la plus avantageuse à chaque étape sans revenir en arrière.
Avantages :
- Simplicité : Les algorithmes gloutons sont souvent plus simples à concevoir et à implémenter.
- Rapidité : Ils sont généralement plus rapides car ils ne considèrent pas de multiples solutions possibles.
Inconvénient :
- Pas toujours optimal : Pour de nombreux problèmes, l'approche gloutonne ne donne pas la solution optimale.
Problème du rendu de monnaie
Vous êtes caissier et vous devez rendre la monnaie sur un achat.
Les dénominations de monnaie disponibles sont :
1 centime, 2 centimes, 5 centimes, 10 centimes, 20 centimes, 50 centimes, 1 euro, et 2 euros.
Vous devez rendre 5,44€ à un client.
Comment pouvez-vous lui rendre la monnaie en utilisant le moins de pièces et billets possible ?
def rendre_monnaie(montant_a_rendre):
denominations_en_centimes = [200, 100, 50, 20, 10, 5, 2, 1]
montant_a_rendre_centimes = int(montant_a_rendre * 100)
resultat = []
for valeur in denominations_en_centimes:
nb_de_denomination = montant_a_rendre_centimes // valeur
if nb_de_denomination > 0:
resultat.append((nb_de_denomination,valeur))
montant_a_rendre_centimes = montant_a_rendre_centimes - valeur * nb_de_denomination
return resultat
# Exemple d'utilisation
montant_a_rendre = 5.44 # 3 euros et 76 centimes
for nb_de_denomination,valeur in rendre_monnaie(montant_a_rendre):
print(f"{nb_de_denomination} pièce(s) de {valeur/100:.2f} euro(s)")2 pièce(s) de 2.00 euro(s) 1 pièce(s) de 1.00 euro(s) 2 pièce(s) de 0.20 euro(s) 2 pièce(s) de 0.02 euro(s)
Problème du sac à dos 0/1 :
wikipedia - Super intéressant !
Vous êtes un aventurier qui prépare son sac à dos pour le retour de son expédition.
Vous avez des objets précieux, chacun avec un poids et une valeur spécifiques.
Cependant, le sac à dos que vous comptez utiliser a une capacité de charge limitée.
Vous devez donc choisir soigneusement quels objets emporter pour maximiser la valeur totale sans dépasser la capacité de poids du sac.
Capacité du sac à dos : 22 kg.
Objets disponibles :
- Objet 1: 60€, poids 6kg
- Objet 2: 63€, poids 7kg
- Objet 3: 66€, poids 8kg
- Objet 4: 69€, poids 9kg
- Objet 5: 70€, poids 7kg
def sac_a_dos_0_1_glouton(capacite, objets):
objets_tries = sorted(objets, key=lambda x: x[0], reverse=True)
valeur_totale = 0
composition_sac = []
poids_actuel = 0
for valeur, poids in objets_tries:
if poids_actuel + poids <= capacite:
composition_sac.append((valeur, poids))
valeur_totale = valeur_totale + valeur
poids_actuel = poids_actuel + poids
print(f"Capacité: {capacite}kg | Solution méthode gloutonne :")
print(f" Valeur max: {valeur_totale}€ | ", end="")
print("Composition sac: ", end ="")
for valeur, poids in composition_sac:
print(f"({valeur}€,{poids}kg), ",end="")
print(f"| Poids: {poids_actuel}kg")
def sac_a_dos_0_1_binaire(capacite, objets):
max_len = len(bin(2**len(objets) - 1)[2:])
meilleure_valeur = 0
solutions = [] # Pour stocker toutes les combinaisons optimales et leurs poids totaux
for i in range(2**len(objets)):
binary = format(i, f'0{max_len}b')
valeur_totale, poids_total = 0, 0
composition_temp = []
for j in range(len(objets)):
if binary[j] == '1':
valeur, poids = objets[j]
poids_total += poids
if poids_total > capacite:
break # Cette combinaison dépasse la capacité
valeur_totale += valeur
composition_temp.append((valeur, poids))
composition_temp.sort(key=lambda x: x[0], reverse=True) # Trier la composition temporaire par valeur décroissante
if poids_total <= capacite and valeur_totale > meilleure_valeur:
meilleure_valeur = valeur_totale
solutions = [(composition_temp, poids_total)] # Stocker également le poids total
elif poids_total <= capacite and valeur_totale == meilleure_valeur:
solutions.append((composition_temp, poids_total))
print(f"Capacité: {capacite}kg | Solution(s) méthode binaire :")
for solution, poids_total in solutions:
print(f" Valeur max: {meilleure_valeur}€ | ", end ="")
print("Composition sac: ", end="")
for valeur, poids in solution:
print(f"({valeur}€,{poids}kg), ", end="")
print(f"| Poids: {poids_total}kg")
# Exemple d'utilisation
objets = [(60, 6), (63, 7), (66, 8), (69, 9), (70,7)]
capacite = 22
sac_a_dos_0_1_glouton(capacite, objets)
sac_a_dos_0_1_binaire(capacite, objets)
print()
# Performance méthode binaire
capacite = 29
sac_a_dos_0_1_glouton(capacite, objets)
sac_a_dos_0_1_binaire(capacite, objets)Capacité: 22kg | Solution méthode gloutonne : Valeur max: 199€ | Composition sac: (70€,7kg), (69€,9kg), (60€,6kg), | Poids: 22kg Capacité: 22kg | Solution(s) méthode binaire : Valeur max: 199€ | Composition sac: (70€,7kg), (66€,8kg), (63€,7kg), | Poids: 22kg Valeur max: 199€ | Composition sac: (70€,7kg), (69€,9kg), (60€,6kg), | Poids: 22kg Capacité: 29kg | Solution méthode gloutonne : Valeur max: 205€ | Composition sac: (70€,7kg), (69€,9kg), (66€,8kg), | Poids: 24kg Capacité: 29kg | Solution(s) méthode binaire : Valeur max: 262€ | Composition sac: (70€,7kg), (69€,9kg), (63€,7kg), (60€,6kg), | Poids: 29kg
- Approche gloutonne :
- complexité spatiale est $O(n)$,
- complexité temporelle de $O(n.log(n))$.
- Approche Binaire :
- complexité spatiale est $O(n.2^n)$,
- complexité temporelle de $O(n.2^n)$.
L'approche gloutonne est beaucoup plus efficace en termes de temps d'exécution par rapport à l'approche binaire. Cependant, l'approche binaire garantit de trouver la solution optimale, tandis que l'approche gloutonne peut ne pas trouver la solution optimale mais offre une bonne solution approchée en un temps nettement plus court.
Programmation dynamique pour le problème du sac à dos 0/1
Le cœur de l'algorithme est le suivant :
-
Initialisation de la matrice K :
K est une matrice de dimensions (n+1) x (capacité+1), où n est le nombre d'objets disponibles.
Chaque élément K[i][w] représente la valeur maximale que l'on peut obtenir avec les i premiers objets et une capacité maximale de w.
La matrice est initialisée avec des zéros. -
Remplissage de la matrice K :
Pour chaque objet i et chaque capacité w, on décide si l'objet i doit être inclus dans le sac à dos ou non.
Si l'objet i peut être inclus (c'est-à-dire, si son poids est inférieur ou égal à la capacité restante w) :
On compare la valeur obtenue en incluant l'objet (objets[i-1][0] + K[i-1][w-objets[i-1][1]]) avec la valeur obtenue sans inclure l'objet (K[i-1][w]).- objets[i-1][0] représente la valeur de l'objet i.
- objets[i-1][1] représente le poids de l'objet i.
- K[i-1][w-objets[i-1][1]] représente la valeur maximale que l'on peut obtenir avec les objets précédents et une capacité restante de w-objets[i-1][1] (capacité restante après avoir inclus l'objet i).
On choisit la valeur maximale des deux pour K[i][w].
- objets[i-1][0] représente la valeur de l'objet i.
-
Trouver la solution :
Après avoir rempli la matrice, la valeur maximale que l'on peut obtenir est stockée dans K[n][capacité].
Pour retrouver les objets qui composent cette solution optimale, on parcourt la matrice à partir de K[n][capacité], en remontant jusqu'à K[0][0], et on identifie les objets qui ont été inclus. -
Retour de la fonction :
La fonction retourne la liste des solutions (dans ce cas, une seule solution est calculée), la valeur maximale obtenue, et la matrice K.
L'expression K[i][w] = max(objets[i-1][0] + K[i-1][w-objets[i-1][1]], K[i-1][w]) est le cœur de l'algorithme de programmation dynamique utilisé pour résoudre le problème. Elle décide si inclure l'objet i dans le sac en comparant la valeur obtenue en l'incluant avec la valeur obtenue sans l'inclure, pour une capacité restante de w. Cela permet de construire progressivement la solution optimale en prenant des décisions locales optimales à chaque étape.
import pandas as pd
def knapsack(capacite, objets):
n = len(objets)
K = [[0 for x in range(capacite + 1)] for x in range(n + 1)]
for i in range(n + 1):
for w in range(capacite + 1):
if i == 0 or w == 0:
K[i][w] = 0
elif objets[i-1][1] <= w:
K[i][w] = max(objets[i-1][0] + K[i-1][w-objets[i-1][1]], K[i-1][w])
else:
K[i][w] = K[i-1][w]
meilleure_valeur = K[n][capacite]
solutions = []
w = capacite
solution_actuelle = []
poids_total_solution = 0
for i in range(n, 0, -1):
if meilleure_valeur <= 0:
break
if meilleure_valeur != K[i-1][w]:
solution_actuelle.append(objets[i-1])
poids_total_solution += objets[i-1][1]
meilleure_valeur -= objets[i-1][0]
w -= objets[i-1][1]
solutions.append((solution_actuelle, poids_total_solution))
meilleure_valeur = K[n][capacite]
return solutions, meilleure_valeur, K
# Exemple d'utilisation
objets = [(60, 6), (63, 7), (66, 8), (69, 9), (70, 7)]
capacite = 29
# Appel de la fonction knapsack
solutions, meilleure_valeur, K = knapsack(capacite, objets)
# Configuration pour augmenter le nombre de lignes et de colonnes affichées
pd.set_option('display.max_rows', None) # Aucune limite pour le nombre de lignes
pd.set_option('display.max_columns', None) # Aucune limite pour le nombre de colonnes
pd.set_option('display.width', None) # Ajuste la largeur pour éviter le retour à la ligne automatique
pd.set_option('display.max_colwidth', None) # Aucune limite pour la largeur de chaque colonne
# Création du DataFrame après l'exécution de knapsack pour éviter les erreurs de dimension
df = pd.DataFrame(K)
df.columns = [f"{w}kg" for w in range(capacite + 1)]
df.index = [f"Objet {i}" for i in range(len(objets) + 1)]
# Affichage du DataFrame complet
print("objets :", objets,'\n')
print(df)
print(f"\nCapacité: {capacite}kg | Solution(s) :")
for solution, poids_total in solutions:
print(f" Valeur max: {meilleure_valeur}€ | ", end="")
print("Composition sac: ", end="")
for valeur, poids in solution:
print(f"({valeur}€,{poids}kg), ", end="")
print(f"| Poids: {poids_total}kg")objets : [(60, 6), (63, 7), (66, 8), (69, 9), (70, 7)]
0kg 1kg 2kg 3kg 4kg 5kg 6kg 7kg 8kg 9kg 10kg 11kg 12kg \
Objet 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Objet 1 0 0 0 0 0 0 60 60 60 60 60 60 60
Objet 2 0 0 0 0 0 0 60 63 63 63 63 63 63
Objet 3 0 0 0 0 0 0 60 63 66 66 66 66 66
Objet 4 0 0 0 0 0 0 60 63 66 69 69 69 69
Objet 5 0 0 0 0 0 0 60 70 70 70 70 70 70
13kg 14kg 15kg 16kg 17kg 18kg 19kg 20kg 21kg 22kg 23kg \
Objet 0 0 0 0 0 0 0 0 0 0 0 0
Objet 1 60 60 60 60 60 60 60 60 60 60 60
Objet 2 123 123 123 123 123 123 123 123 123 123 123
Objet 3 123 126 129 129 129 129 129 129 189 189 189
Objet 4 123 126 129 132 135 135 135 135 189 192 195
Objet 5 130 133 136 139 139 139 139 193 196 199 202
24kg 25kg 26kg 27kg 28kg 29kg
Objet 0 0 0 0 0 0 0
Objet 1 60 60 60 60 60 60
Objet 2 123 123 123 123 123 123
Objet 3 189 189 189 189 189 189
Objet 4 198 198 198 198 198 198
Objet 5 205 205 205 205 259 262
Capacité: 29kg | Solution(s) :
Valeur max: 262€ | Composition sac: (70€,7kg), (69€,9kg), (63€,7kg), (60€,6kg), | Poids: 29kg
L'algorithme knapsack du sac à dos a une complexité temporelle et spatiale de $O(n.capacite)$.
Programmation recursive pour le problème du sac à dos 0/1
def sac_a_dos_0_1_recursive_simple(capacite, objets):
if capacite == 0 or not objets:
return 0
else:
valeur, poids = objets[0] # Considère le premier objet de la liste
if poids > capacite:
# Si l'objet actuel est trop lourd, passe au suivant sans l'ajouter
return sac_a_dos_0_1_recursive_simple(capacite, objets[1:])
else:
# Compare la valeur de l'inclusion de l'objet actuel avec celle de son exclusion
return max(valeur + sac_a_dos_0_1_recursive_simple(capacite - poids, objets[1:]), sac_a_dos_0_1_recursive_simple(capacite, objets[1:]))
# Exemple d'utilisation
objets = [(60, 6), (63, 7), (66, 8), (69, 9), (70, 7)]
capacite = 22
print(f"Capacité: {capacite}kg | {sac_a_dos_0_1_recursive_simple(capacite, objets)} €")
capacite = 29
print(f"Capacité: {capacite}kg | {sac_a_dos_0_1_recursive_simple(capacite, objets)} €")Capacité: 22kg | 199 € Capacité: 29kg | 262 €
L'algorithme récursif du sac à dos a une complexité temporelle $O(2^n)$ et une complexité spatiale de $O(n)$.
# Récursivité avec affichage de toutes les solutions
def sac_a_dos_0_1_recursive(capacite, objets, solution_actuelle=[]):
if capacite <= 0 or not objets:
return 0, [solution_actuelle]
else:
premier_objet = objets[0]
exclure_valeur, exclure_solutions = sac_a_dos_0_1_recursive(capacite, objets[1:], solution_actuelle)
if premier_objet[1] > capacite:
return exclure_valeur, exclure_solutions
else:
inclure_valeur, inclure_solutions = sac_a_dos_0_1_recursive(capacite - premier_objet[1], objets[1:], solution_actuelle + [premier_objet])
inclure_valeur += premier_objet[0]
if inclure_valeur > exclure_valeur:
return inclure_valeur, inclure_solutions
elif inclure_valeur < exclure_valeur:
return exclure_valeur, exclure_solutions
else:
return inclure_valeur, inclure_solutions + exclure_solutions
def afficher_solutions(capacite, objets):
valeur_max, solutions = sac_a_dos_0_1_recursive(capacite, objets)
solutions_uniques = [list(t) for t in {tuple(s) for s in solutions}] # Enlever les doublons
print(f"Capacité: {capacite}kg | Solution(s) optimale(s) :")
for solution in solutions_uniques:
poids_total = sum(poids for _, poids in solution)
print(f" Valeur max: {valeur_max}€ | Composition sac: ", end="")
for valeur, poids in solution:
print(f"({valeur}€,{poids}kg), ", end="")
print(f"| Poids: {poids_total}kg")
print()
# Exemple d'utilisation
objets = [(60, 6), (63, 7), (66, 8), (69, 9), (70, 7)]
capacite = 22
afficher_solutions(capacite, objets)
capacite = 29
afficher_solutions(capacite, objets)
Capacité: 22kg | Solution(s) optimale(s) : Valeur max: 199€ | Composition sac: (63€,7kg), (66€,8kg), (70€,7kg), | Poids: 22kg Valeur max: 199€ | Composition sac: (60€,6kg), (69€,9kg), (70€,7kg), | Poids: 22kg Capacité: 29kg | Solution(s) optimale(s) : Valeur max: 262€ | Composition sac: (60€,6kg), (63€,7kg), (69€,9kg), (70€,7kg), | Poids: 29kg