 Sommaire : Terminale_ipynb
Sommaire : Terminale_ipynb
1.2 - Piles, Files, Listes
1.3 - Dictionnaires
1.4 - Arbres
1.5 - Graphes
2.1 - SQL Modèle relationnel ✔
2.2 - SQL Requêtes ✔
3.1 - Système sur puce
3.2 - Processus, système
3.3 - Routage
3.4 - Congruences
3.5 - RSA
4.1 - Programme en tant que donnée
4.2 - Récursivité ✔
4.3 - Modularité
4.4 - Paradigmes de programmation
4.5 - Gestion des bugs
5.1 - Algorithme Graphes
5.2 - Diviser pour régner ✔
5.3 - Programmation dynamique
5.4 - Recherche textuelle
01 - Hanoï ✔
02 - Hanoï (Correction) ✔
03 - Jeu 1 ✔
03 - Jeu 2 ✔
01 - POO, Piles, Files, Listes, Dictionnaires
02 - Arbre
03 - Graphe
04 - SQL
05 - Routage
06 - Récursivité et Diviser pour régner
07 - Système sur Puce et Processus Système
08 - Modularité
09 - Tri par insertion, tri par selection
10 - Les congruences
1.1 - Implémentation, POO ✔
Structures de données
Structures de données, interface et implémentation - Vocabulaire de la programmation objet : classes, attributs, méthodes, objets.
Compétences attendues :
Spécifier une structure de données par son interface.
Distinguer interface et implémentation.
Écrire plusieurs implémentations d’une même structure de données.
Écrire la définition d’une classe.
Accéder aux attributs et méthodes d’une classe.
Commentaires:
L’abstraction des structures de données est introduite après plusieurs implémentations d’une structure simple comme la file
(avec un tableau ou avec deux piles)
On n’aborde pas ici tous les aspects de la programmation objet comme le polymorphisme et l’héritage.
1. Qu'est-ce qu'une structure de données ?
Une structure de données est un moyen d'organiser, de stocker et de manipuler des données dans un ordinateur de manière efficace.
Les structures de données permettent de gérer de grandes quantités de données, d'effectuer des opérations complexes et d'optimiser la vitesse et la mémoire utilisée.
Exemple :
Imaginez une bibliothèque. Sans un système organisé, il serait très difficile de trouver un livre. Les structures de données sont comme ces systèmes qui permettent de classer et de trouver rapidement des livres.
2. Interface vs Implémentation
Interface: C'est ce que vous voyez et utilisez comme utilisateur de la structure de données. L'interface définit les opérations que l'on peut effectuer sur la structure sans spécifier comment elles sont réalisées. Par exemple, pour une liste, l'interface pourrait inclure des fonctions comme "ajouter", "supprimer" ou "trouver", mais elle ne dirait pas comment ces fonctions sont implémentées.
Exemple:
Imaginons une machine à café. Les boutons pour choisir le type de café (expresso, cappuccino) et la taille de la tasse constituent l'interface. Vous n'avez pas besoin de savoir comment la machine produit le café, vous devez juste appuyer sur le bouton désiré.
Implémentation: C'est la manière concrète dont la structure de données est réalisée ou codée. Il peut y avoir plusieurs implémentations pour une même interface. Par exemple, une liste peut être implémentée comme un tableau ou comme une liste chaînée, mais pour l'utilisateur de cette liste, l'implémentation est souvent transparente.
Exemple:
Dans la machine à café, l'implémentation serait le mécanisme interne qui moud les grains, fait chauffer l'eau, et infuse le café selon votre sélection.
3. Pourquoi faire la distinction ?
Séparer l'interface de l'implémentation offre plusieurs avantages:
Modularité: Les développeurs peuvent changer l'implémentation d'une structure de données sans affecter les utilisateurs de cette structure, tant que l'interface reste la même.
Exemple :
Si le mécanisme interne de la machine à café tombe en panne, on peut le remplacer sans changer les boutons que les utilisateurs utilisent.
Abstraction: Les utilisateurs n'ont pas besoin de connaître les détails de l'implémentation pour utiliser la structure. Cela rend le code plus propre et plus facile à comprendre.
Exemple :
En tant qu'utilisateur, vous n'avez pas besoin de comprendre comment le café est préparé, vous appuyez simplement sur un bouton. C'est le principe d'abstraction.
Flexibilité: Si une implémentation particulière présente des problèmes de performance ou d'autres problèmes dans un contexte spécifique, elle peut être remplacée par une autre implémentation sans que les utilisateurs de la structure aient à changer leur code.
Exemple :
Si le propriétaire de la machine à café veut changer la marque des grains de café ou la méthode de chauffage de l'eau, il peut le faire sans que l'utilisateur ne le remarque.
4. Exemples courants de structures de données
-
Tableaux (Arrays): Une collection d'éléments identifiés par des indices ou des clés.
Exemple :Pensez à une étagère de livres où chaque livre est identifié par son numéro de position.
-
Listes chaînées (Linked Lists): Une collection d'éléments, où chaque élément pointe vers le suivant dans la liste.
Exemple :Imaginez une chasse au trésor où chaque indice vous conduit au suivant.

Piles (Stacks): Une collection d'éléments avec une politique de dernier entré, premier sorti (LIFO).
Exemple : Imaginez une pile d'assiettes; la dernière assiette que vous placez est la première que vous retirez.

-
Files (Queues): Une collection d'éléments avec une politique de premier entré, premier sorti (FIFO).
Exemple : Pensez à une file d'attente à la caisse d'un supermarché. Le premier client en ligne sera le premier servi.
-
Arbres (Trees): Une structure hiérarchique d'éléments avec un élément racine et des sous-éléments.
Exemple : Imaginez l'organigramme d'une entreprise. Le PDG est à la racine, et les employés sont organisés en niveaux hiérarchiques.
-
Graphes (Graphs): Un ensemble d'éléments connectés par des arêtes.
Exemple : Pensez à un réseau social où chaque personne est un point, et les liens d'amitié sont les connexions entre ces points.
Chaque structure a sa propre interface et peut avoir de nombreuses implémentations différentes.
L'essentiel est de comprendre que les structures de données, à travers leurs interfaces, nous permettent d'interagir avec des informations et des données sans nécessairement savoir comment elles sont stockées ou manipulées à l'arrière-plan (l'implémentation).
5. Programmation Orientée Objet
POO" est l'acronyme de "Programmation Orientée Objet" (en anglais : "OOP" pour "Object-Oriented Programming").
La POO est un paradigme de programmation qui utilise des "objets" et des classes pour organiser le code. Elle se base sur plusieurs concepts clés :
-
Objets : Un
objetest une entité qui regroupe desdonnéeset desfonctionsqui opèrent sur ces données. Chaque objet est uneinstance d'une classe. -
Classes : Une
classeest un modèle duquel les objets sont créés. Elle définit desattributs (données)et desméthodes (fonctions). -
Encapsulation : L'
encapsulationest leregroupement des données et des méthodes qui opèrent sur ces données en une seule unité (l'objet). Elle permet aussi de restreindre l'accès direct à certains composants de l'objet. -
Abstraction : L'
abstractionpermet decacher la complexité en ne montrant que les fonctionnalités essentiellesd'un objet. Cela aide à réduire la complexité et à augmenter l'efficacité.
La POO offre de nombreux avantages, tels que la modularité, la réutilisabilité du code et une structure claire, ce qui facilite la maintenance et l'évolution du code.
Exemple : Voici comment nous pourriez implémenter une file (queue) avec un tableau (list en Python)
class FileAvecTableau: # Classe structure qui permet de définir des objets qui encapsulent des données et des fonctions.
def __init__(self): # __init__: constructeur appelée lors de la création d'une nouvelle instance d'une classe.
# self est un paramètre qui fait référence à l'instance actuelle
self.queue = [] # attribut interne de l'objet ou de l'instance
def enfile(self, item): # Méthode
self.queue.append(item)
def defile(self): # Méthode
if not self.est_vide():
return self.queue.pop(0)
else:
raise IndexError("Defile d'une file vide.")
def est_vide(self): # Méthode
return len(self.queue) == 0
def taille(self):
return len(self.queue)
def __str__(self): #__str__: Méthode appelée par print() ou str() pour obtenir une représentation de l'objet.
return str(self.queue)
ma_file = FileAvecTableau() # Créez une instance de la classe.
ma_file.enfile("Pierre")
ma_file.enfile("Paul")
ma_file.enfile("jacque")
print(ma_file.taille())
print(ma_file)
print(ma_file.defile())
print(ma_file)
print(ma_file.taille())
print(ma_file.est_vide())3 ['Pierre', 'Paul', 'jacque'] Pierre ['Paul', 'jacque'] 2 False
ma_valise = FileAvecTableau() # Création d'une autre instance avec la même classe.
ma_valise.enfile("Chemise")
ma_valise.enfile("Pullover")
ma_valise.enfile("Chaussettes")
ma_valise.enfile("Tee-shirt")
ma_valise.enfile("maillot")
print(ma_valise.taille())
print(ma_valise)
print(ma_valise.defile())
print(ma_valise)
print(ma_valise.taille())
print(ma_valise.est_vide())5 ['Chemise', 'Pullover', 'Chaussettes', 'Tee-shirt', 'maillot'] Chemise ['Pullover', 'Chaussettes', 'Tee-shirt', 'maillot'] 4 False
Vidéo : Le paramètre self
Exemple : Voici comment faire la même implémentetion d'une file (queue) avec avec 2 piles
class FileAvecDeuxPiles:
def __init__(self):
self.pile1 = [] # Pile pour l'enfilage
self.pile2 = [] # Pile pour le défilage
def enfile(self, item):
self.pile1.append(item)
def defile(self):
if not self.pile2: # Si la pile2 est vide
while self.pile1: # Renverser la pile1 dans pile2
self.pile2.append(self.pile1.pop())
if not self.pile2: # Si la pile2 est toujours vide après le renversement
raise IndexError("Defile d'une file vide.")
return self.pile2.pop()
def est_vide(self):
return not self.pile1 and not self.pile2
def taille(self):
return len(self.pile1) + len(self.pile2)
def __str__(self):
return str(self.pile2[::-1] + self.pile1)
ma_file = FileAvecDeuxPiles() # Créez une instance de la classe.
ma_file.enfile("Pierre")
ma_file.enfile("Paul")
ma_file.enfile("jacque")
print(ma_file.taille())
print(ma_file)
print(ma_file.defile())
print(ma_file)
print(ma_file.taille())
print(ma_file.est_vide())3 ['Pierre', 'Paul', 'jacque'] Pierre ['Paul', 'jacque'] 2 False
Autres exemples :
Exemple 1 :
Créez une classe Personne qui a des attributs pour le nom, age et sexe de la personne. La classe doit également avoir une méthode se_presenter() qui affiche une brève introduction de la personne.
class Personne:
def __init__(self, nom, age, sexe):
self.nom = nom # Attribue externe
self.age = age
self.sexe = sexe
def se_presenter(self):
print(f"Bonjour, je m'appelle {self.nom}. J'ai {self.age} ans et je suis un {self.sexe}.")
# Test
p = Personne("Jean", 30, "homme")
p.se_presenter()Bonjour, je m'appelle Jean. J'ai 30 ans et je suis un homme.
Exemple 2 :
Créez une classe Cercle qui prend un rayon comme attribut et a deux méthodes, l'une pour calculer la surface (surface) et l'autre pour calculer le périmètre (perimetre).
import math
class Cercle:
def surface(self, rayon):
return math.pi * rayon ** 2
def perimetre(self, rayon):
return 2 * math.pi * rayon
# Test
c = Cercle()
print(f"Surface: {c.surface(5)}")
print(f"Périmètre: {c.perimetre(5)}")
Surface: 78.53981633974483 Périmètre: 31.41592653589793
import math
class Cercle:
def __init__(self, rayon):
self.rayon = rayon
def surface(self):
return math.pi * self.rayon ** 2
def perimetre(self):
return 2 * math.pi * self.rayon
# Test
c = Cercle(5)
print(f"Surface: {c.surface()}")
print(f"Périmètre: {c.perimetre()}")Surface: 78.53981633974483 Périmètre: 31.41592653589793
import math
class Cercle:
def __init__(self):
pass
def definir_rayon(self, rayon):
self.rayon = rayon
def surface(self):
if self.rayon is None:
raise ValueError("Rayon non défini")
return math.pi * self.rayon ** 2
def perimetre(self):
if self.rayon is None:
raise ValueError("Rayon non défini")
return 2 * math.pi * self.rayon
# Test
c = Cercle()
c.definir_rayon(5) # Définir le rayon avant d'appeler les méthodes
print(f"Surface: {c.surface()}")
print(f"Périmètre: {c.perimetre()}")
Surface: 78.53981633974483 Périmètre: 31.41592653589793
Exemple 3:
Créez une classe Voiture qui a des attributs pour la marque, modele, et kilometrage. Ajoutez une méthode afficher_details() pour afficher les détails de la voiture et une autre méthode conduire() pour augmenter le kilométrage.
class Voiture:
def __init__(self, marque, modele, kilometrage):
self.marque = marque
self.modele = modele
self.kilometrage = kilometrage
def afficher_details(self):
print(f"Voiture {self.marque} {self.modele}, {self.kilometrage} km parcourus.")
def conduire(self, km):
self.kilometrage += km
# Test
v = Voiture("Peugeot", "208", 10000)
v.afficher_details()
v.conduire(150)
v.afficher_details()
Voiture Peugeot 208, 10000 km parcourus. Voiture Peugeot 208, 10150 km parcourus.
Exercices :
Exercice 1 :
Créez une classe Rectangle qui prend la largeur et la hauteur comme attributs. Cette classe devrait avoir des méthodes pour calculer la surface (surface) et le périmètre (perimetre).
Exercice 2 :
Définissez une classe Points qui représente deux points dans un espace 2D : $A(x_1, y_1)$ et $B(x_2, y_2)$.
La classe doit avoir les méthodes suivantes :
vecteur(): Renvoie les coordonnées du vecteur $\vec{AB}$.milieu(): Renvoie les coordonnées du point milieu du segment $[AB]$.distance(): Calcule la distance entre $A$ et $B$.equation_reduite(): Renvoie l'équation réduite de la droite passant par $A$ et $B$.equation_cercle(): Renvoie l'équation du cercle dont $[AB]$ est le diamètre.
Pour tester votre solution, vous pouvez utiliser les points $A(0,0)$ et $B(2,2)$ avec p = Points(0, 0, 2, 2)
class Rectangle:
def __init__(self, largeur, hauteur):
self.largeur = largeur
self.hauteur = hauteur
def surface(self):
return self.largeur * self.hauteur
def perimetre(self):
return 2 * (self.largeur + self.hauteur)
# Test
r = Rectangle(4, 6)
print(f"Surface: {r.surface()}")
print(f"Périmètre: {r.perimetre()}")
Surface: 24 Périmètre: 20
from math import *
class Rectangle:
def __init__(self):
pass
def set_longueur(self, longueur):
self.longueur = longueur
def set_largeur(self, largeur):
self.largeur = largeur
def surface(self):
return self.largeur * self.longueur
def perimetre(self):
return (2 * self.largeur) + (2* self.longueur)
# Test
r = Rectangle()
r.set_longueur(2)
r.set_largeur(1)
print(f"Surface: {r.surface()}")
print(f"Périmètre: {r.perimetre()}")Surface: 2 Périmètre: 6
import math
class Points:
def __init__(self, x1, y1, x2, y2):
self.x1 = x1
self.y1 = y1
self.x2 = x2
self.y2 = y2
def vecteur(self):
return (self.x2 - self.x1, self.y2 - self.y1)
def milieu(self):
return ((self.x1 + self.x2) / 2, (self.y1 + self.y2) / 2)
def distance(self):
return math.sqrt((self.x2 - self.x1)**2 + (self.y2 - self.y1)**2)
def equation_reduite(self):
if self.x2 - self.x1 == 0:
return f"x = {self.x1}"
m = (self.y2 - self.y1) / (self.x2 - self.x1)
p = self.y1 - m * self.x1
return f"y = {m:.2f}x + {p:.2f}"
def equation_cercle(self):
h, k = self.milieu()
r = self.distance() / 2
return f"(x - {h:.2f})^2 + (y - {k:.2f})^2 = {r**2:.2f}"
# Test
p = Points(0, 0, 2, 2)
print("Vecteur AB:", p.vecteur())
print("Milieu de [AB]:", p.milieu())
print(f"Distance AB: {p.distance():.2f}")
print("Equation réduite de la droite (AB):", p.equation_reduite())
print("Equation du cercle de diamètre [AB]:", p.equation_cercle())
Vecteur AB: (2, 2) Milieu de [AB]: (1.0, 1.0) Distance AB: 2.83 Equation réduite de la droite (AB): y = 1.00x + 0.00 Equation du cercle de diamètre [AB]: (x - 1.00)^2 + (y - 1.00)^2 = 2.00
1.2 - Piles, Files, Listes
Structures de données
Listes, piles, files : structures linéaires.
compétences attendues :
Distinguer des structures par le jeu des méthodes qui les caractérisent.
Choisir une structure de données adaptée à la situation à modéliser.
commentaires :
On distingue les modes FIFO (first in first out) et LIFO (last in first out) des piles et des files.
1) Introduction
De nombreux algorithmes "classiques" manipulent des structures de données plus complexes que des simples nombres. Nous allons ici voir quelques structures de données. Nous allons commencer par des types de structures relativement simples : les listes, les piles et les files. Ces trois types de structures sont qualifiés de linéaires.
2) Les piles
On retrouve dans les piles une partie des propriétés vues sur les listes. Dans les piles, il est uniquement possible de manipuler le dernier élément introduit dans la pile. On prend souvent l'analogie avec une pile d'assiettes : dans une pile d'assiettes la seule assiette directement accessible et la dernière assiette qui a été déposée sur la pile.

Les piles sont basées sur le principe LIFO (Last In First Out : le dernier rentré sera le premier à sortir).
On retrouve souvent ce principe LIFO en informatique.
Voici les opérations que l'on peut réaliser sur une pile :
- savoir si une pile est vide (estVide)
- empiler un nouvel élément sur la pile (empiler en français, push en anglais)
- récupérer l'élément au sommet de la pile tout en le supprimant. On dit que l'on dépile (dépiler en français, pop en anglais)
- connaitre le nombre d'éléments présents dans la pile (taille)
Exemples :
Soit une pile P composée des éléments suivants :
22 (le sommet de la pile est 22)
19
7
8
14
12dépile(P) renvoie 22 et la pile P est maintenant composée des éléments suivants :
19
7
8
14
12taille(P) renvoie 5 empiler(42) la pile P est maintenant composée des éléments suivants :
42
19
7
8
14
12si on applique dépiler(P) 6 fois de suite, estVide(P) renvoie vrai
Implémentation d'une pile
-
On utilise ici le paradigme de la programmation objet, mais ce n'est pas la seule façon de faire.
-
L'implémentation se fait aisément à l'aide du type
listde python, en particulier avec les méthodes suivantes :- La méthode
append()qui ajoute un élément en fin de liste. - La méthode
pop()qui supprime le dernier élément d'une liste, en le renvoyant. - la méthode
len()qui renvoie la longueur d'une liste c'est à dire son nombre d'éléments.
- La méthode
-
Quelques rappels :
- L'indice
-1permet d'accéder au dernier élément d'une liste. []est la liste vide.
- L'indice
class Pile:
def __init__(self):
self.items = []
def estvide(self):
return len(self.items) == 0
def empiler(self, item):
self.items.append(item)
def depiler(self):
if self.estvide():
print("La pile est vide!")
else:
element_depile = self.items.pop()
#print(f"Élément dépilé : {element_depile}")
#print()
return element_depile
def sommet(self):
if self.estvide():
print("La pile est vide!")
else:
return self.items[-1]
def taille(self):
print(f"Taille : {len(self.items)}")
print()
return len(self.items)
def afficher(self):
for item in reversed(self.items):
print(f"{item:2}")
print()
# Exemple d'utilisation
p = Pile()
p.empiler(12)
p.empiler(14)
p.empiler(8)
p.empiler(7)
p.empiler(19)
p.empiler(22)
p.afficher()
p.depiler()
p.afficher()
p.taille()
p.empiler(42)
p.afficher()
p.depiler()
p.depiler()
p.depiler()
p.depiler()
p.depiler()
p.depiler()
p.estvide()
22 19 7 8 14 12 19 7 8 14 12 Taille : 5 42 19 7 8 14 12
3) les files
Comme les piles, les files ont des points communs avec les listes.
Différences majeures : dans une file on ajoute des éléments à une extrémité de la file et on supprime des éléments à l'autre extrémité.
On prend souvent l'analogie de la file d'attente devant un magasin pour décrire une file de données.

Les files sont basées sur le principe FIFO (First In First Out : le premier qui est rentré sera le premier à sortir. Ici aussi, on retrouve souvent ce principe FIFO en informatique.
Voici les opérations que l'on peut réaliser sur une file :
- savoir si une file est vide (estVide)
- ajouter un nouvel élément à la file (enfiler en français, enqueue en anglais)
- récupérer l'élément situé en bout de file tout en le supprimant (défiler en français, dequeue en anglais)
- connaitre le nombre d'éléments présents dans la file (taille)
Exemples :
Soit une file F composée des éléments suivants : 12 → 14 → 8 → 7 → 19 → 22
(le premier élément rentré dans la file est 22 ; le dernier élément rentré dans la file est 12)
12 → 14 → 8 → 7 → 19 → 22
enfiler(42) : la file F est maintenant 42 → 12 → 14 → 8 → 7 → 19 → 22
taille(F) renvoie 6
défiler(F) renvoie 22 ,la file F est maintenant : 42 → 12 → 14 → 8 → 7 → 19
défiler(F) 6 fois de suite
estVide(F) renvoie vrai
class File:
def __init__(self):
self.elements = []
def estVide(self):
return len(self.elements) == 0
def enfiler(self, element):
self.elements.append(element)
def defiler(self):
if self.estVide():
print("La file est vide !")
return None
else:
return self.elements.pop(0)
def taille(self):
return len(self.elements)
def afficher(self):
for i, elem in enumerate(reversed(self.elements)):
if i == len(self.elements) - 1:
print(elem, end="")
else:
print(f"{elem} -> ", end="")
print()# Test
F = File()
F.enfiler(22)
F.enfiler(19)
F.enfiler(7)
F.enfiler(8)
F.enfiler(14)
F.enfiler(12)
F.afficher() # Doit afficher 12 → 14 → 8 → 7 → 19 → 22
print(F.taille()) # Doit afficher : 6
F.enfiler(42)
F.afficher() # Doit afficher 42 → 12 → 14 → 8 → 7 → 19 → 22
print(F.defiler()) #Doit afficher 22
F.afficher() # Doit afficher 42 → 12 → 14 → 8 → 7 → 19
# Appliquer défile(F) 6 fois
for _ in range(6):
F.defiler()
print(F.estVide()) # Doit afficher : True12 -> 14 -> 8 -> 7 -> 19 -> 22 6 42 -> 12 -> 14 -> 8 -> 7 -> 19 -> 22 22 42 -> 12 -> 14 -> 8 -> 7 -> 19 True
4) Les listes
Une liste est une structure de données permettant de regrouper des données. Une liste L est composée de 2 parties :
- sa tête (souvent noté car), qui correspond au dernier élément ajouté à la liste,
- et sa queue (souvent noté cdr) qui correspond au reste de la liste. queue → ... → tête ou cdr → ... → car
Le langage de programmation Lisp, inventé par John McCarthy en 1958, a été un des premiers langages de programmation à introduire cette notion de liste. Lisp signifie "list processing".
Voici les opérations qui peuvent être effectuées sur une liste :
- tester si une liste est vide
- ajoute un nouvel élément en tête
- obtenir le dernier élément ajouté à la liste
- supprime le dernier élément ajouté
queue → ... → tête
class Liste:
def __init__(self):
self.elements = []
def estVide(self):
return len(self.elements) == 0
def ajouter(self, element):
self.elements.append(element)
def dernier_element(self):
if self.estVide():
print("La liste est vide !")
return None
else:
return self.elements[-1]
def retirer(self):
if self.estVide():
print("La liste est vide !")
return None
else:
return self.elements.pop(-1)
def taille(self):
return len(self.elements)
def __str__(self):
if not self.elements:
return "nil"
else:
result = str(self.elements[0])
for elem in self.elements[1:]:
result += " → " + str(elem)
return resultl = Liste()
print(l.estVide()) # Affiche: True
l.ajouter(12)
print(l) # Affiche 12
print(l.estVide()) # Affiche: False
l.ajouter(15) # Ajoute 15 en tête
print(l) # Affiche 12 → 15
l.ajouter(11)
l.ajouter(1)
print(l) # Affiche 12 → 15 → 11 → 1
print(l.dernier_element()) # Affiche 1 mais ne le retire pas de la liste
l.retirer() # Retire 1
print(l) # Affiche 12 → 15 → 11
print(l.taille()) # # Affiche 3True 12 False 12 → 15 12 → 15 → 11 → 1 1 12 → 15 → 11 3
5) Types abstraits et représentation concrète des données
Nous avons évoqué ci-dessus la manipulation des types de données (liste, pile et file) par des algorithmes, mais, au-delà de la beauté intellectuelle de réfléchir sur ces algorithmes, le but de l'opération est souvent, à un moment ou un autre, de "traduire" ces algorithmes dans un langage compréhensible pour un ordinateur (Python, Java, C,...).
On dit alors que l'on implémente un algorithme.
Il est donc aussi nécessaire d'implémenter les types de données comme les listes, les piles ou les files afin qu'ils soient utilisables par les ordinateurs.
Les listes, les piles ou les files sont des "vues de l'esprit" présentes uniquement dans la tête des informaticiens, on dit que ce sont des types abstraits de données (ou plus simplement des types abstraits).
L'implémentation de ces types abstraits, afin qu'ils soient utilisables par une machine, est loin d'être une chose triviale. L'implémentation d'un type de données dépend du langage de programmation. Il faut, quel que soit le langage utilisé, que le programmeur retrouve les fonctions qui ont été définies pour le type abstrait (pour les listes, les piles et les files cela correspond aux fonctions définies ci-dessus). Certains types abstraits ne sont pas forcément implémentés dans un langage donné, si le programmeur veut utiliser ce type abstrait, il faudra qu'il le programme par lui-même en utilisant les "outils" fournis par son langage de programmation.
Pour implémenter les listes (ou les piles et les files), beaucoup de langages de programmation utilisent 2 structures : les tableaux et les listes chaînées.
Un tableau est une suite contiguë de cases mémoires (les adresses des cases mémoire se suivent). Le système réserve une plage d'adresse mémoire afin de stocker des éléments.
La taille d'un tableau est fixe : une fois que l'on a défini le nombre d'éléments que le tableau peut accueillir, il n'est pas possible modifier sa taille. Si l'on veut insérer une donnée, on doit créer un nouveau tableau plus grand et déplacer les éléments du premier tableau vers le second tout en ajoutant la donnée au bon endroit !
Dans certains langages de programmation, on trouve une version "évoluée" des tableaux : les tableaux dynamiques. Les tableaux dynamiques ont une taille qui peut varier. Il est donc relativement simple d'insérer des éléments dans le tableau. Ce type de tableaux permet d'implémenter facilement le type abstrait liste (de même pour les piles et les files).
À noter que les "listes Python" (listes Python) sont des tableaux dynamiques. Attention de ne pas confondre avec le type abstrait liste défini ci-dessus, ce sont de "faux amis".
6) Choisir une structure de données adaptée à la situation à modéliser.
Exemple 1 : Utilisation de la classe Pile pour la vérification d'équilibre de parenthèses.
pile = Pile()
def check_parentheses(expr):
for char in expr:
if char == "(":
pile.empiler(char)
elif char == ")":
if pile.estvide():
return False
pile.depiler()
return pile.estvide()
expr = "((1 + 2) * (3 + 4)*2)"
result = check_parentheses(expr)
print(f"Les parenthèses sont équilibrées: {result}")
Les parenthèses sont équilibrées: True
Exemple 2 : Utilisation de la classe File pour la gestion d'une file d'attente pour un guichet de banque.
file = File()
def serve_clients():
while not file.estVide():
client = file.defiler()
print(f"Serving client {client}")
# Ajout de clients dans la file
file.enfiler("Alice")
file.enfiler("Bob")
file.enfiler("Charlie")
# Servir les clients
serve_clients()
Serving client Alice Serving client Bob Serving client Charlie
Exemple 3 : Utilisation de la classe Liste pour trouver le dernier élément ajouté à la liste.
liste = Liste()
# Ajout d'éléments
liste.ajouter(5)
liste.ajouter(10)
liste.ajouter(15)
# Trouver le dernier élément ajouté
dernier = liste.dernier_element()
print(f"Le dernier élément ajouté est {dernier}")
# Afficher la liste
print("La liste actuelle est:", liste)
Le dernier élément ajouté est 15 La liste actuelle est: 5 → 10 → 15
Exemple 4 : Distibution d'un jeu de carte à 2 joueus
from random import shuffle
# Jeu de 32 cartes
cartes = [i + j for i in ['7', '8', '9', '10', 'V', 'D', 'R', 'A'] for j in ["♠", "♥", "♦", "♣"]]
shuffle(cartes)
# Initialisation du jeu complet
jeu = Pile()
for carte in cartes:
jeu.empiler(carte)
# Afficher le jeu complet
print('Jeu complet :')
jeu.afficher()
print()
# Distribution des cartes (piles)
jeu1 = Pile()
jeu2 = Pile()
while not jeu.estvide():
carte = jeu.depiler()
if carte:
jeu1.empiler(carte)
carte = jeu.depiler()
if carte:
jeu2.empiler(carte)
# Afficher les deux jeux de cartes après distribution
print("Jeu du joueur 1:")
jeu1.afficher()
print("\nJeu du joueur 2:")
jeu2.afficher()
Jeu complet 7♠ R♦ D♥ 10♣ 7♦ 7♣ 9♥ 9♣ 7♥ V♣ 8♠ D♣ 8♦ V♦ D♦ R♠ R♣ 10♥ 10♦ A♠ 8♣ A♣ 9♦ A♥ 8♥ 9♠ D♠ 10♠ R♥ V♥ V♠ A♦ Jeu du joueur 1: V♠ R♥ D♠ 8♥ 9♦ 8♣ 10♦ R♣ D♦ 8♦ 8♠ 7♥ 9♥ 7♦ D♥ 7♠ Jeu du joueur 2: A♦ V♥ 10♠ 9♠ A♥ A♣ A♠ 10♥ R♠ V♦ D♣ V♣ 9♣ 7♣ 10♣ R♦
1.3 - Dictionnaires
Structures de données
Dictionnaires, index et clé
Capacités attendus :
Distinguer la recherche d’une valeur dans une liste et dans un dictionnaire.
Entrainement
1) Dictionnaires
Un dictionnaire est une structure de données qui stocke des paires clé-valeur.
Chaque clé est unique et chaque clé est associée à une valeur.
Voici comment vous pouvez créer un dictionnaire en Python :
mon_dictionnaire = {
"nom": "Alice",
"age": 30,
"email": "alice@email.com"
}
print(mon_dictionnaire){'nom': 'Alice', 'age': 30, 'email': 'alice@email.com'}
un_autre_dictionnaire = dict(nom='Bob', age=40, email='bob@email.com')
print(un_autre_dictionnaire){'nom': 'Bob', 'age': 40, 'email': 'bob@email.com'}
Pour accéder aux valeurs en utilisant leurs clés correspondantes :
print(mon_dictionnaire["nom"])
print(mon_dictionnaire["age"]) Alice 30
Pour modifier les valeurs associées aux clés :
mon_dictionnaire["age"] = 31
print(mon_dictionnaire["age"]) 31
Pour ajouter de nouvelles paires clé-valeur au dictionnaire :
mon_dictionnaire["adresse"] = "123 rue du Paradis"
print(mon_dictionnaire){'nom': 'Alice', 'age': 31, 'email': 'alice@email.com', 'adresse': '123 rue du Paradis'}
Pour supprimer une paire clé-valeur, utilisez le mot-clé del :
del mon_dictionnaire["adresse"]
print(mon_dictionnaire){'nom': 'Alice', 'age': 31, 'email': 'alice@email.com'}
Pour afficher la taille d'un dictionnaire :
print(len(mon_dictionnaire))3
Itérer sur les clés
for cle in mon_dictionnaire:
print(cle)nom age email
autre méthode :
cles = mon_dictionnaire.keys()
print(cles)
# Pour convertir en liste
liste_cles = list(cles)
print(liste_cles) dict_keys(['nom', 'age', 'email']) ['nom', 'age', 'email']
Itérer sur les valeurs
for valeur in mon_dictionnaire.values():
print(valeur)Alice 31 alice@email.com
autre méthode :
valeurs = mon_dictionnaire.values()
print(valeurs)
# Pour convertir en liste
liste_valeurs = list(valeurs)
print(liste_valeurs) dict_values(['Alice', 31, 'alice@email.com']) ['Alice', 31, 'alice@email.com']
Itérer sur les clés et les valeurs
for cle, valeur in mon_dictionnaire.items():
print(f"{cle} : {valeur}")nom : Alice age : 30 email : alice@email.com
Pour rechercher une valeur dans un dictionnaire en Python
"Alice" in mon_dictionnaire.values()valeur_recherchée = "Alice"
for valeur in mon_dictionnaire.values():
if valeur == valeur_recherchée:
print(f"La valeur '{valeur_recherchée}' a été trouvée dans le dictionnaire.")
breakLa valeur 'Alice' a été trouvée dans le dictionnaire.
autre méthode :valeur_recherchée = "Alice"
for cle, valeur in mon_dictionnaire.items():
if valeur == valeur_recherchée:
print(f"La valeur '{valeur_recherchée}' a été trouvée dans le dictionnaire avec la clé '{cle}'.")
break
La valeur 'Alice' a été trouvée dans le dictionnaire avec la clé 'nom'.
2) Index
L'index est un autre concept en programmation, généralement associé aux tableaux ou aux listes.
Une liste est une collection ordonnée d'éléments, qui peut contenir des données de types différents.
Contrairement aux dictionnaires, les éléments d'un tableau sont accessibles par leur position, ou index, qui commence généralement par 0.
ma_liste = ['Alice', 31, 'alice@email.com', 'adresse']
print(ma_liste[0])
print(ma_liste[1])
print(ma_liste[-1])
print(ma_liste[-2])
print(ma_liste[1:]) # Afficher la liste à partir de l'indice 1
print(ma_liste[1:3]) # Afficher la liste à partir de l'indice 1 à 2 !!!
print(ma_liste[:-1]) # Afficher la liste sauf le dernierAlice 31 adresse alice@email.com [31, 'alice@email.com', 'adresse'] [31, 'alice@email.com'] ['Alice', 31, 'alice@email.com']
Pour changer une valeur dans la liste, assignez une nouvelle valeur à l'index correspondant.
ma_liste[0] = 10
print(ma_liste)[10, 31, 'alice@email.com', 'adresse']
Pour afficher la taille d'une liste :
print(len(mon_liste))Pour rechercher une valeur dans une liste en Python
'alice@email.com' in ma_listeautre méthode :
valeur_recherchée = 'alice@email.com'
for i, valeur in enumerate(ma_liste):
if valeur == valeur_recherchée:
print(f"La valeur {valeur_recherchée} est trouvée à l'indice {i}.")
breakLa valeur alice@email.com est trouvée à l'indice 2.
3) Différence entre clés et index
La principale différence entre les clés d'un dictionnaire et les index d'une liste est que les clés sont généralement des chaînes de caractères qui représentent le sens sémantique des valeurs, tandis que les index sont des entiers qui représentent la position des valeurs dans la liste.
4) P-uplets nommés
En Python, les p-uplets nommés peuvent être implémentés par des dictionnaires ou par collections.namedtuple.
personnes = {
'Alice': {'age': 30, 'email': 'alice@email.com'},
'Bob': {'age': 40, 'email': 'bob@email.com'},
'Charlie': {'age': 50, 'email': 'charlie@email.com'}
}
print(personnes['Alice'])
print(personnes['Alice']['age']){'age': 30, 'email': 'alice@email.com'}
30
from collections import namedtuple
# Définition du p-uplet nommé
Personne = namedtuple('Personne', ['nom', 'age', 'email'])
# Création d'une instance du p-uplet nommé
alice = Personne(nom='Alice', age=30, email='alice@email.com')
bob = Personne(nom='Bob', age=40, email='bob@email.com')
charlie = Personne(nom='Charlie', age=50, email='charlie@email.com')
print(alice)
print(alice.nom)
print(alice.age)Personne(nom='Alice', age=30, email='alice@email.com') Alice 30
Les données EXIF d'une image
Les données EXIF (Exchangeable Image File Format) d'une image peuvent être représentées sous forme de dictionnaire.
Par exemple, pour lire les données EXIF d'une image, on utilise la bibliothèque PIL.

Télécharger l'image ci-dessus est collée importe là dans ce fichier basthon
from PIL import Image
image = Image.open("Pieds_du_femme_dans_le_metro.jpg")
exif_data = image._getexif()
print(exif_data){34853: {0: b'\x02\x02\x00\x00', 1: 'N', 2: (41.0, 24.0, 9.66), 3: 'E', 4: (2.0, 9.0, 9.9), 18: 'WGS-84'}, 296: 2, 34665: 202, 271: 'Sony', 272: 'G8441', 305: '47.1.A.16.20_0_a600', 274: 1, 306: '2018:10:25 09:07:03', 282: 72.0, 283: 72.0, 36864: b'0231', 37121: b'\x01\x02\x03\x00', 37377: 5.64, 36867: '2018:10:25 09:07:03', 36868: '2018:10:25 09:07:03', 37380: 0.0, 40960: b'0100', 37383: 5, 37384: 0, 37385: 16, 37386: 4.4, 40961: 1, 40962: 1024, 41988: 1.0, 41990: 0, 41996: 0, 37520: '991195', 37521: '991195', 37522: '991195', 40963: 576, 33434: 0.02, 33437: 2.0, 41985: 0, 34855: 500, 41986: 0, 41987: 0}
for cle, valeur in exif_data.items():
print(f"{cle} : {valeur}")34853 : {0: b'\x02\x02\x00\x00', 1: 'N', 2: (41.0, 24.0, 9.66), 3: 'E', 4: (2.0, 9.0, 9.9), 18: 'WGS-84'}
296 : 2
34665 : 202
271 : Sony
272 : G8441
305 : 47.1.A.16.20_0_a600
274 : 1
306 : 2018:10:25 09:07:03
282 : 72.0
283 : 72.0
36864 : b'0231'
37121 : b'\x01\x02\x03\x00'
37377 : 5.64
36867 : 2018:10:25 09:07:03
36868 : 2018:10:25 09:07:03
37380 : 0.0
40960 : b'0100'
37383 : 5
37384 : 0
37385 : 16
37386 : 4.4
40961 : 1
40962 : 1024
41988 : 1.0
41990 : 0
41996 : 0
37520 : 991195
37521 : 991195
37522 : 991195
40963 : 576
33434 : 0.02
33437 : 2.0
41985 : 0
34855 : 500
41986 : 0
41987 : 0
exif_data[34853]exif_data[34853][1],exif_data[34853][2],exif_data[34853][3],exif_data[34853][4]1.4 - Arbres
Structures de données
Arbres : structures hiérarchiques.
Arbres binaires : nœuds, racines,feuilles,sous-arbres gauches,sous-arbres droits.
Capacités Attendue :
- Identifier des situations nécessitant une structure de données arborescente.
- Évaluer quelques mesures des arbres binaires (taille,encadrement de la hauteur, etc...).
Commentaires :
On fait le lien avec la rubrique « algorithmique »
Algorithmes sur les arbres binaires et sur les arbres binaires de recherche.
Capacités Attendue :
- Calculer la taille et la hauteur d’un arbre.
- Parcourir un arbre de différentes façons (ordres infixe, préfixe ou suffixe ; ordre en largeur d’abord).
- Rechercher une clé dans un arbre de recherche, insérer une clé.
Commentaires :
- Une structure de données récursive adaptée est utilisée.
- L’exemple des arbres permet d’illustrer la programmation par classe.
- La recherche dans un arbre de recherche équilibré est de coût logarithmique.
Les arbres en informatique sont des structures de données qui représentent une hiérarchie sous forme d'une collection de nœuds reliés par des arêtes.
Ces structures évoquent l'image d'un arbre vu à l'envers, où la racine se situe en haut et les branches s'étendent vers le bas. Chaque nœud a un parent (à l'exception de la racine) et zéro ou plusieurs enfants.
La nature hiérarchique des arbres les rend extrêmement utiles pour représenter des structures de données organisées de manière non linéaire.
Par exemples :
- les systèmes de fichiers d'un ordinateur sont souvent organisés comme un arbre, avec un dossier racine contenant des sous-dossiers, qui eux-mêmes peuvent contenir d'autres sous-dossiers, et ainsi de suite.
- les pages web peuvent être analysées en utilisant un arbre pour représenter la structure du Document Object Model (DOM). - les arbres sont aussi couramment utilisés pour les algorithmes de recherche et de tri, comme les arbres binaires de recherche ( BTS ou Binary Search Tree , les arbres AVL, ou encore les arbres B.
Leur structure hiérarchique permet d'effectuer des opérations de recherche, d'insertion et de suppression de manière très efficace, souvent en temps logarithmique.
Les arbres sont donc une pierre angulaire de l'organisation et du traitement des données en informatique.
1. Arbres binaires : nœuds, racines,feuilles,sous-arbres gauches,sous-arbres droits.
Définition :
Un arbre binaire est une structure de données hiérarchique dans laquelle :
-
Chaque
nœudaau plus deux enfants, souvent désignés comme lesous-arbre gaucheet lesous-arbre droit. -
Chaque
nœudcontient unevaleuret deux pointeurs vers ses enfants gauche et droit. -
Le nœud de départ de l'arbre. Il n'a pas de parent, s'appelle la
Racine. -
Un nœud qui n'a pas d'enfants, s'appelle
Feuille.
Un arbre binaire de recherche est une structure de données hiérarchique dans laquelle on a aussi :
Tous les éléments à gauche d'un nœud donné sont plus petits que la valeur du nœud.Tous les éléments à droite d'un nœud donné sont plus grands que la valeur du nœud.
Un arbre binaire est dit complet si tous ses niveaux, à l'exception peut-être du dernier, sont entièrement remplis, et tous les nœuds du dernier niveau sont aussi à gauche que possible.
class Noeud:
def __init__(self, valeur, gauche=None, droit=None):
self.valeur = valeur
self.gauche = gauche
self.droit = droit
racine = Noeud(40)
n20 = Noeud(20)
n60 = Noeud(60)
n10 = Noeud(10)
n30 = Noeud(30)
n50 = Noeud(50)
n70 = Noeud(76)
n5 = Noeud(5)
n15 = Noeud(15)
n25 = Noeud(25)
n35 = Noeud(35)
n45 = Noeud(45)
n75 = Noeud(75)
n80 = Noeud(80)
# Assemblage de l'arbre
racine.gauche = n20
racine.droit = n60
n20.gauche = n10
n20.droit = n30
n60.gauche = n50
n60.droit = n70
n10.gauche = n5
n10.droit = n15
n30.gauche = n25
n30.droit = n35
n50.gauche = n45
n70.gauche = n75
n70.droit = n80
def est_arbre_binaire(noeud, gauche=None, droite=None):
if noeud is None:
return True
if gauche and noeud.valeur <= gauche.valeur:
print(f"Problème : {noeud.valeur} <= {gauche.valeur} !!!")
return False
if droite and noeud.valeur >= droite.valeur:
print(f"Problème : {noeud.valeur} => {droite.valeur} !!!")
return False
return (est_arbre_binaire(noeud.gauche, gauche, noeud) and
est_arbre_binaire(noeud.droit, noeud, droite))
def verifier(racine):
if not est_arbre_binaire(racine):
print("L'arbre n'est pas un arbre binaire de recherche valide.")
else:
print("L'arbre est un arbre binaire de recherche valide.")
verifier(racine)
# Dessin de l'arbre
from graphviz import Digraph
from IPython.display import display, SVG
def dessiner_arbre(noeud, graph=None):
if graph is None:
graph = Digraph()
if noeud is not None:
graph.node(str(noeud.valeur))
if noeud.gauche:
graph.node(str(noeud.gauche.valeur))
graph.edge(str(noeud.valeur), str(noeud.gauche.valeur))
dessiner_arbre(noeud.gauche, graph)
if noeud.droit:
graph.node(str(noeud.droit.valeur))
graph.edge(str(noeud.valeur), str(noeud.droit.valeur))
dessiner_arbre(noeud.droit, graph)
return graph
def arbre_visuel(racine) :
graph = dessiner_arbre(racine)
raw_data = graph.pipe(format='svg')
raw_text = raw_data.decode('utf-8')
display(SVG(data=raw_text))
arbre_visuel(racine)Définitions Métriques :
- La taille de l'arbre est le nombre total de nœuds.
- La hauteur de l'arbre est le nombre d'arêtes de la racine au nœud le plus profond .
- La profondeur d'un nœud est le nombre d'arêtes de la racine à ce nœud.
Exemple : Dans notre arbre ci-dessus :
- La taille est 14.
- La hauteur est 3.
# Fonction pour calculer la taille de l'arbre
def taille_arbre(noeud):
if noeud is None:
return 0
return 1 + taille_arbre(noeud.gauche) + taille_arbre(noeud.droit)
# Fonction pour calculer la hauteur de l'arbre
def hauteur_arbre(noeud):
if noeud is None:
return -1 # On commence à -1 pour que le nœud racine n'ajoute pas 1 à la hauteur totale
return 1 + max(hauteur_arbre(noeud.gauche), hauteur_arbre(noeud.droit))
# Calcul de la taille et de la hauteur
taille = taille_arbre(racine)
hauteur = hauteur_arbre(racine)
# Affichage
print(f"La taille de l'arbre est de {taille} nœuds.")
print(f"La hauteur de l'arbre est de {hauteur}.")Rappel : Pour tout $x>0$, on a : $log_2(x)=\frac{ln(x)}{ln(2)}$
Formules :
- La hauteur maximale pour un arbre avec $n$ nœuds : $n−1$ .
- La hauteur minimale pour un arbre avec $n$ nœuds : $log_2(n)$.(Ordre de grandeur !!!)
Démonstration :
- Hauteur maximale :
Dans le pire des cas, chaque nœud de l'arbre a seulement un enfant.
Cela donne une structure "en ligne", où chaque nouveau nœud ajoute une unité à la hauteur de l'arbre.
Par conséquent, si vous avez $n$ nœuds, la hauteur maximale de l'arbre serait $n-1$.
- Hauteur minimale :
Dans le meilleur des cas, l'arbre est parfaitement équilibré, c'est-à-dire un arbre binaire complet. Chaque niveau $k$ de l'arbre contient $2^k$ nœuds. Par conséquent, la hauteur minimale $h$ est déterminée par le nombre total de nœuds $n$ que l'on peut distribuer sur ces niveaux :
$\sum_{k=0}^{h} 2^k = n$
$\iff 1 + 2 + 2^2 + 2^3 + \cdots + 2^h = n$
$\iff \frac{2^{h+1} - 1}{2 - 1} = n$
$\iff 2^{h+1} - 1 = n$
$\iff 2^{h+1} = n + 1$
$\iff h+1 = \log_2(n + 1)$
$\iff h = \log_2(n + 1) - 1$
Le résultat n'est pas exactement $log_2(n)$, mais il est proche et donne un ordre de grandeur pour la hauteur minimale.
Défintion : Parcours en profondeur d'un arbre
Dans un parcours en profondeur (Depth-First Search ou DFS en anglais), vous partez de la racine de l'arbre et explorez aussi loin que possible le long de chaque branche avant de revenir en arrière. Il existe trois types de parcours en profondeur :
A
/ \
B C
/ \ / \
D E F G
/ \ / \ / \ / \
H I J K L M N O-
Préfixe (Préordre) (Root, Left, Right):
Vous visitez d'abord la racine, puis vous parcourez récursivement tous les sous-arbres gauches et enfin tous les sous-arbres droits.
Exemple Préordre : A, B, D, H, I, E, J, K, C, F, L, M, G, N, O -
Infixe (Inordre) (Left, Root, Right):
Vous parcourez d'abord récursivement tous les sous-arbres gauches, vous visitez la racine, puis vous parcourez récursivement tous les sous-arbres droits.
Exemple Inordre : H, D, I, B, J, E, K, A, L, F, M, C, N, G, O -
Suffixe (Postordre) (Left, Right, Root):
Vous parcourez d'abord récursivement tous les sous-arbres gauches, puis tous les sous-arbres droits, et enfin la racine.
Exemple Postordre : H, I, D, J, K, E, B, L, M, F, N, O, G, C, A
Définition : Parcours en largeur d'un arbre
Dans un parcours en largeur (Breadth-First Search ou BFS en anglais), vous visitez tous les nœuds d'un niveau donné avant de passer au niveau suivant. Cela commence généralement à la racine. Exemple Parcours en largeur : A, B, C, D, E, F, G, H, I, J, K, L, M, N, O
# Parcours en largeur
def parcours_en_largeur(racine):
file, result = [racine], []
while file:
noeud = file.pop(0)
result.append(noeud.valeur)
if noeud.gauche:
file.append(noeud.gauche)
if noeud.droit:
file.append(noeud.droit)
return "".join(result)
# Parcours en profondeur
def Préfixe(noeud):
if noeud is not None:
return str(noeud.valeur) + Préfixe(noeud.gauche) + Préfixe(noeud.droit)
else:
return ""
def Infixe(noeud):
if noeud is not None:
return Infixe(noeud.gauche) + str(noeud.valeur) + Infixe(noeud.droit)
else:
return ""
def Suffixe(noeud):
if noeud is not None:
return Suffixe(noeud.gauche) + Suffixe(noeud.droit) + str(noeud.valeur)
else:
return ""
racine_lettre = Noeud('A', Noeud('B', Noeud('D', Noeud('H'), Noeud('I')), Noeud('E', Noeud('J'), Noeud('K'))), Noeud('C', Noeud('F', Noeud('L'), Noeud('M')), Noeud('G', Noeud('N'), Noeud('O'))))
print("Parcours en largeur : ", parcours_en_largeur(racine_lettre))
print("Parcours en Préfixe : ", Préfixe(racine_lettre))
print("Parcours en Infixe : ", Infixe(racine_lettre))
print("Parcours en Suffixe : ", Suffixe(racine_lettre))
arbre_visuel(racine_lettre)Rechercher une clé dans un arbre de recherche
La recherche dans un arbre de recherche binaire commence à la racine et descend dans l'arbre en comparant la clé à celle dans le nœud actuel. Puis on se dirige soit vers le sous-arbre gauche, soit vers le sous-arbre droit selon que la clé est plus petite ou plus grande que celle du nœud actuel.
def recherche(noeud, cle):
if noeud is None:
print(f"Clé {cle} non trouvée dans l'arbre.")
return
if cle == noeud.valeur:
print(f"Clé {cle} trouvée dans l'arbre.")
return
elif cle < noeud.valeur:
return recherche(noeud.gauche, cle)
else:
return recherche(noeud.droit, cle)
arbre_visuel(racine)
recherche(racine, 76)Insérer une clé.
# Insérer un nœud dans l'arbre
n42 = Noeud(42)
n47 = Noeud(47)
n45.gauche = n42
n45.droit = n47
# Affichage des parcours
arbre_visuel(racine)
verifier(racine)La recherche dans un arbre de recherche équilibré est de coût logarithmique.
complexité $O(n)$ et complexité $O(log (n))$
La notation $O(n)$ et $O(log n)$ expriment comment la performance d'un algorithme évolue en fonction de la taille de l'entrée n.
La complexité $O(n)$ signifie que le temps d'exécution de votre algorithme est $T(n)$=a $n$+b, où T(n) est le temps d'exécution et a et b sont des constantes.
La complexité $O(log (n))$ signifie que le temps d'exécution de votre algorithme est $T(n)$=a $log(n)$+b, où T(n) est le temps d'exécution et a et b sont des constantes.
La notation $O(log (n))$ est un indicateur d'algorithmes très efficaces, plus que $O(n)$
La recherche dans un arbre binaire de recherche (ABR) équilibré est effectivement de coût logarithmique en termes de complexité temporelle. Plus précisément, cette complexité est de $O(log(n))$, où $n$ est le nombre de nœuds dans l'arbre.
L'équilibrage de l'arbre est crucial pour maintenir cette performance optimale. Si l'arbre est déséquilibré, la complexité de recherche peut se dégrader vers $O(n)$ dans le pire des cas, où $n$ est également le nombre de nœuds.
Il existe des variantes d'arbres binaires de recherche qui s'auto-équilibrent pour maintenir cette complexité logarithmique, tels que les arbres AVL et les arbres rouge-noir. Ces structures s'assurent que l'arbre reste équilibré après chaque insertion ou suppression, garantissant ainsi que les opérations de recherche, d'insertion et de suppression s'exécutent toutes en temps logarithmique.
L'arbre AVL (Adelson-Velsky et Landis) est un arbre binaire de recherche qui maintient l'équilibre en gardant la différence de hauteur entre les sous-arbres gauche et droit de chaque nœud à 1 ou 0.
# Création de nouvel arbre binaire de recherche
racine2 = Noeud(30)
n20 = Noeud(20)
n40 = Noeud(40)
n10 = Noeud(10)
n5 = Noeud(5)
racine2.gauche = n20
racine2.droit = n40
n20.gauche = n10
n10.gauche = n5
arbre_visuel(racine2)class Noeud:
def __init__(self, valeur):
self.valeur = valeur
self.hauteur = 1
self.gauche = None
self.droit = None
def get_hauteur(n):
if not n:
return 0
return n.hauteur
def get_balance(n):
if not n:
return 0
return get_hauteur(n.gauche) - get_hauteur(n.droit)
def rotation_droite(y):
x = y.gauche
T3 = x.droit
x.droit = y
y.gauche = T3
y.hauteur = max(get_hauteur(y.gauche), get_hauteur(y.droit)) + 1
x.hauteur = max(get_hauteur(x.gauche), get_hauteur(x.droit)) + 1
return x
def rotation_gauche(x):
y = x.droit
T2 = y.gauche
y.gauche = x
x.droit = T2
x.hauteur = max(get_hauteur(x.gauche), get_hauteur(x.droit)) + 1
y.hauteur = max(get_hauteur(y.gauche), get_hauteur(y.droit)) + 1
return y
def equilibrer_avl_auto(n):
if not n:
return None
n.gauche = equilibrer_avl_auto(n.gauche)
n.droit = equilibrer_avl_auto(n.droit)
n.hauteur = 1 + max(get_hauteur(n.gauche), get_hauteur(n.droit))
balance = get_balance(n)
if balance > 1:
if get_balance(n.gauche) >= 0:
return rotation_droite(n)
else:
n.gauche = rotation_gauche(n.gauche)
return rotation_droite(n)
if balance < -1:
if get_balance(n.droit) <= 0:
return rotation_gauche(n)
else:
n.droit = rotation_droite(n.droit)
return rotation_gauche(n)
return n
# Votre arbre initial
racine2 = Noeud(30)
n20 = Noeud(20)
n40 = Noeud(40)
n10 = Noeud(10)
n5 = Noeud(5)
racine2.gauche = n20
racine2.droit = n40
n20.gauche = n10
n10.gauche = n5
print("Arbre d'origine :")
arbre_visuel(racine2)
racine2 = equilibrer_avl_auto(racine2) # Équilibrage automatique de l'arbre
print("Arbre équilibré :")
arbre_visuel(racine2)
1.5 - Graphes
Structures de données
Graphes : structures relationnelles.
Sommets, arcs, arêtes, graphes orientés ou non orientés.
Capacités Attendue :
- Modéliser des situations sous forme de graphes.
- Écrire les implémentations correspondantes d’un graphe : matrice d’adjacence, liste de successeurs/de prédécesseurs.
- Passer d’une représentation à une autre.
Commentaires :
- On s’appuie sur des exemples comme le réseau routier, le réseau électrique, Internet, les réseaux sociaux.
- Le choix de la représentation dépend du traitement qu’on veut mettre en place : on fait le lien avec la rubrique « algorithmique ».
1. Notion de graphe et vocabulaire
Le concept de graphe permet de résoudre de nombreux problèmes en mathématiques comme en informatique. C'est un outil de représentation très courant, et nous l'avons déjà rencontré à plusieurs reprises, en particulier lors de l'étude de réseaux.
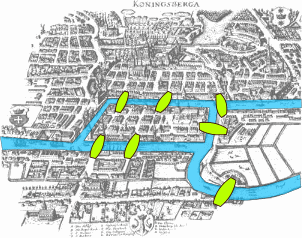
Le problème des sept ponts de Königsberg est connu pour être à l'origine de la topologie et de la théorie des graphes. Résolu par Leonhard Euler en 1735, ce problème mathématique se présente de la façon suivante :
 ➡
➡
 ➡
➡
La ville de Königsberg (aujourd'hui Kaliningrad) est construite autour de deux îles situées sur le Pregel et reliées entre elles par un pont. Six autres ponts relient les rives de la rivière à l'une ou l'autre des deux îles, comme représentés sur le plan ci-dessus. Le problème consiste à déterminer s'il existe ou non une promenade dans les rues de Königsberg permettant, à partir d'un point de départ au choix, de passer une et une seule fois par chaque pont, et de revenir à son point de départ, étant entendu qu'on ne peut traverser le Pregel qu'en passant sur les ponts.
1.1 Exemples de situations : Réseau informatique, Réseau de transport, Réseau social...

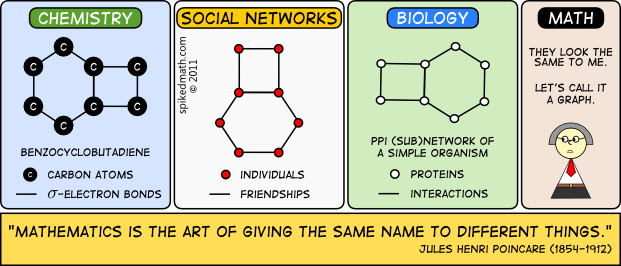
Une multitude de problèmes concrets d'origines très diverses peuvent donner lieu à des modélisations par des graphes : c'est donc une structure essentielle en sciences, qui requiert un formalisme mathématique particulier que nous allons découvrir.
L'étude de la théorie des graphes est un champ très vaste des mathématiques : nous allons surtout nous intéresser à l'implémentation en Python d'un graphe et à différents problèmes algorithmiques qui se posent dans les graphes.
1.2 Vocabulaire
En général, un graphe est un ensemble d'objets, appelés sommets ou nœuds (vertex or nodes en anglais) reliés par des arêtes ou arcs (edges en anglais). Un graphe peut être non-orienté ou orienté .
1.2.1 Graphe non-orienté
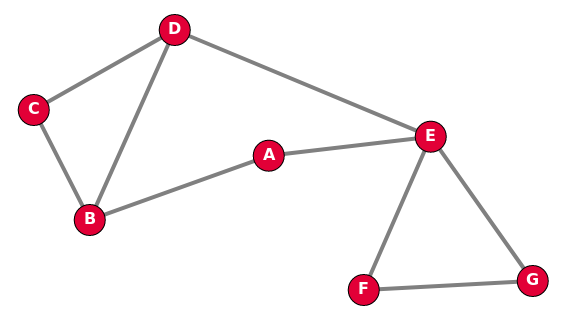
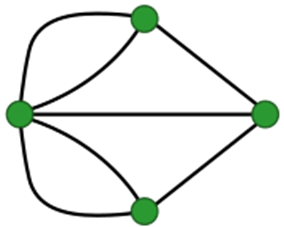
Dans un graphe non-orienté, les arêtes peuvent être empruntées dans les deux sens, et une chaîne est une suite de sommets reliés par des arêtes, comme C - B - A - E par exemple. La longueur de cette chaîne est alors 3, soit le nombre d'arêtes.
Les sommets B et E sont adjacents au sommet A, ce sont les voisins de A.
Exemple de graphe non-orienté : le graphe des relations d'un individu sur Facebook est non-orienté.
1.2.2 Graphe orienté
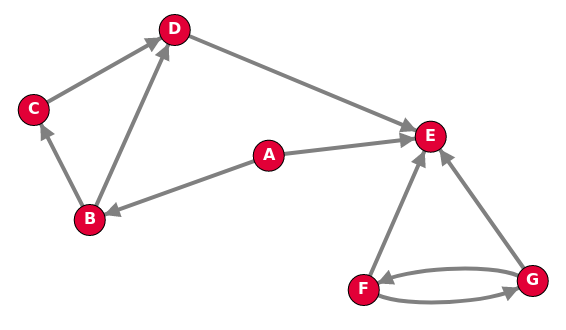
Dans un graphe orienté, les arrêtes ne peuvent être empruntés que dans le sens de la flèche, et un chemin est une suite de sommets reliés par des arcs, comme B → C → D → E par exemple.
Les sommets C et D sont adjacents au sommet B (mais pas A !), ce sont les voisins de B.
Exemple de graphe orienté : le graphe des relations d'un individu sur Twitter est orienté, car on peut suivre une personne sans que elle nous suive.
1.2.3 Graphe pondéré
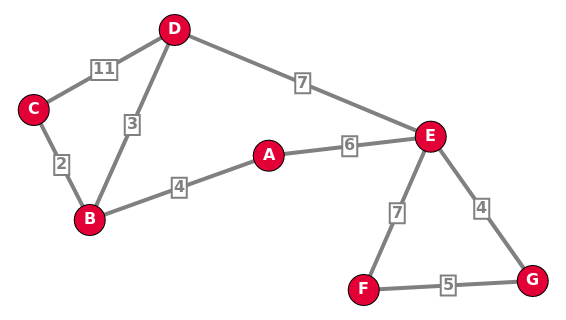
Un graphe est pondéré (ou valué) si on attribue à chaque arête une valeur numérique (la plupart du temps positive), qu'on appelle mesure, poids, coût ou valuation.
Par exemple:
- dans le protocole OSPF, on pondère les liaisons entre routeurs par le coût;
- dans un réseau routier entre plusieurs villes, on pondère par les distances.
1.2.4 Connexité
Un graphe est connexe si n'importe quelle paire de sommets peut toujours être reliée par une chaîne.
Par exemple, le graphe précédent est connexe.
Mais le suivant ne l'est pas: il n'existe pas de chaîne entre les sommets A et F par exemple.
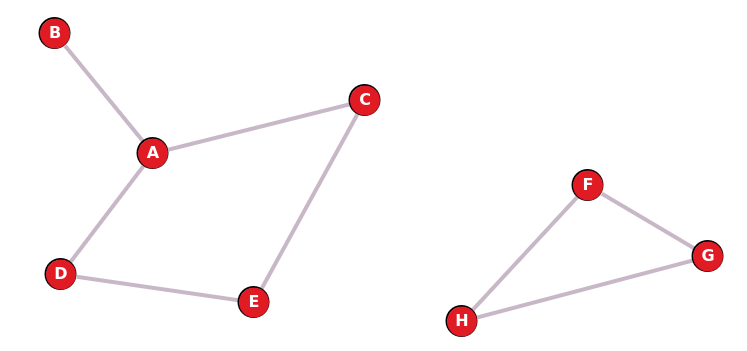 Il possède cependant deux composantes connexes : le sous-graphe composé des sommets A, B, C, D et E d'une part et le sous-graphe composé des sommets F, G et H.
Il possède cependant deux composantes connexes : le sous-graphe composé des sommets A, B, C, D et E d'une part et le sous-graphe composé des sommets F, G et H.2. Modélisations d'un graphe
2.1 Représentation par matrice d'adjacence
Principe : On représente les arêtes (ou les arcs) dans une matrice, c'est-à-dire un tableau à deux dimensions où on inscrit un 1 en ligne i et colonne j si les sommets de rang i et de rang j sont adjacents. Ce tableau s'appelle une matrice d'adjacence (on aurait très bien pu l'appeler aussi matrice de voisinage).
Graphe non orienté :

Graphe orienté :
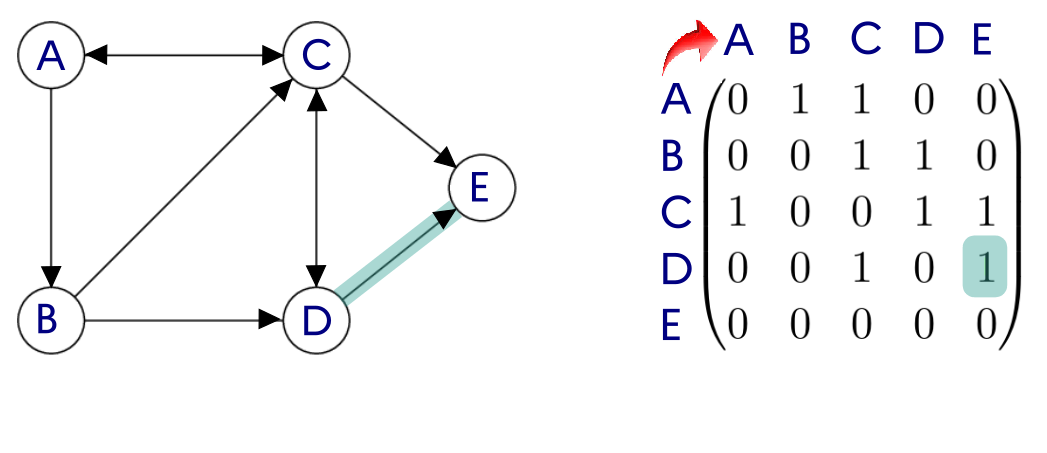
Graphe pondéré :
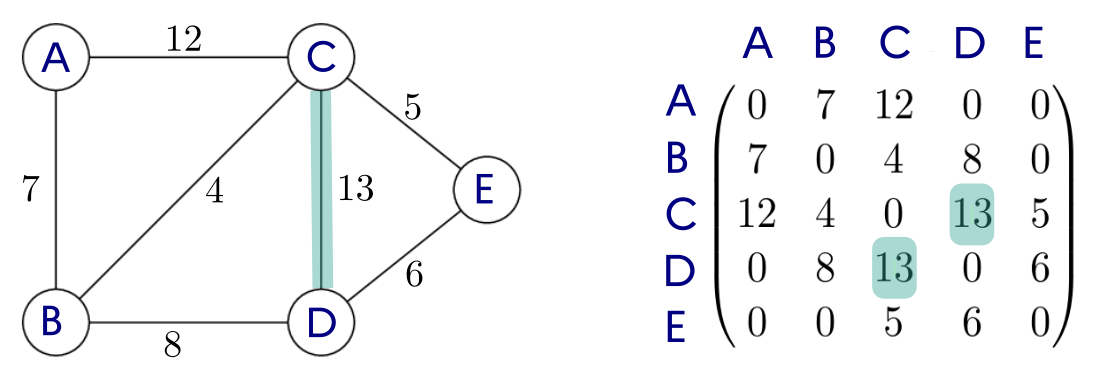
2.2 Liste de successeurs, liste de prédécesseurs
Dans un graphe :
- la
liste de successeursest une liste de tous les nœuds vers lesquels une arête sort de ce nœud donné.
- la
liste de prédécesseurspour un nœud donné est une liste de tous les nœuds qui ont une arête menant à ce nœud.
Exemple :

matrice_adjacence = [[0, 1, 0, 0, 0],
[0, 0, 1, 0, 1],
[0, 1, 0, 1, 0],
[0, 0, 0, 0, 0],
[1, 0, 0, 0, 0]]
noms_sommets = ['A', 'B', 'C', 'D' , 'E']
Liste des successeurs : {'A': ['B'], 'B': ['C', 'E'], 'C': ['B', 'D'], 'D': [], 'E': ['A']}
Liste des prédécesseurs : {'A': ['E'], 'B': ['A', 'C'], 'C': ['B'], 'D': ['C'], 'E': ['B']}A partir de la liste des successeurs, dessiner un graph possible. De même avec la liste des prédécesseurs.
3. Création d'une classe Graphe pour les graphes avec la matrice adjacente
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
class Graphe_Matrice_Adjacente:
def __init__(self, matrice_adjacence, noms_sommets):
self.matrice_adjacence = np.array(matrice_adjacence)
self.noms_sommets = noms_sommets
def liste_successeurs(self):
liste_succ = {}
n = len(self.matrice_adjacence)
for i in range(n):
successeurs = []
for j in range(n):
if self.matrice_adjacence[i][j]:
successeurs.append(self.noms_sommets[j])
liste_succ[self.noms_sommets[i]] = successeurs
return liste_succ
def liste_predecesseurs(self):
liste_pred = {}
n = len(self.matrice_adjacence)
for j in range(n):
predecesseurs = []
for i in range(n):
if self.matrice_adjacence[i][j]:
predecesseurs.append(self.noms_sommets[i])
liste_pred[self.noms_sommets[j]] = predecesseurs
return liste_pred
def afficher(self, figsize=(3, 3)):
plt.figure(figsize=figsize)
G = nx.DiGraph()
edge_labels = {}
for i, nom_sommet in enumerate(self.noms_sommets):
for j, poids in enumerate(self.matrice_adjacence[i]):
if poids != 0:
G.add_edge(nom_sommet, self.noms_sommets[j], weight=poids)
edge_labels[(nom_sommet, self.noms_sommets[j])] = poids
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, font_weight='bold', node_color='skyblue', font_size=12, node_size=500, arrows=True)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
plt.show()
# Création d'un graphe avec la matrice d'adjacence donnée
matrice_adjacence = [[0, 5, 8, 0],
[0, 0, 0, 0],
[0, 3, 0, 6],
[7, 0, 0, 0]]
noms_sommets = ['A', 'B', 'C', 'D']
# Instanciation de la classe Graphe_Matrice_Adjacente
graphe = Graphe_Matrice_Adjacente(matrice_adjacence, noms_sommets)
print("Liste des successeurs :",graphe.liste_successeurs())
print("Liste des prédécesseurs :",graphe.liste_predecesseurs())
graphe.afficher()Liste des successeurs : {'A': ['B', 'C'], 'B': [], 'C': ['B', 'D'], 'D': ['A']}
Liste des prédécesseurs : {'A': ['D'], 'B': ['A', 'C'], 'C': ['A'], 'D': ['C']}
4. Que raconte le cours de math de terminale

2.1 - SQL Modèle relationnel ✔
NSI - Terminale - Bases de données
Modèle relationnel :
relation, attribut, domaine, clef primaire, clef étrangère, schéma relationnel
Capacités attendues : Identifier les concepts définissant le modèle relationnel.
Commentaires : Ces concepts permettent d’exprimer les contraintes d’intégrité (domaine, relation et référence).
1) Introduction
Les bases de données permettent de stocker des données. Pour manipuler les données présentes dans une base de données (écrire, lire ou encore modifier), il est nécessaire d'utiliser un type de logiciel appelé "système de gestion de base de données" très souvent abrégé en SGBD.
- Les SGBD permettent de gérer la lecture, l'écriture ou la modification des informations contenues dans une base de données
- les SGBD permettent de gérer les autorisations d'accès à une base de données.
- les SGBD assurent la maintenance des différentes copies de la base de données (en cas de panne d’un ordinateur), on parle de redondance des données.
- les problèmes d'accès concurrent (plusieurs personnes connectées en même temps) sont gérés par les SGBD.
Par rapport à une base de données, le stockage de données dans un fichier de type CSV est beaucoup plus simple à mettre en place, mais aussi beaucoup plus limité : pas de contrôle d’accès, pas de redondance des données, pas de gestion des accès concurrents.
Il existe différents types de bases de données, par exemple, les bases de données hiérarchiques, les bases de données objet, les bases de données nosql ou bien encore les bases de données relationnelles. Les bases de données relationnelles sont le plus utilisées au monde, c'est ce type de base de données que nous allons étudier.
Les bases de données relationnelles ont été mises au point en 1970 par Edgar Franck Codd, informaticien britannique (1923-2003). Ces bases de données sont basées sur la théorie mathématique des ensembles.
2) Relation
La notion de relation est au coeur des bases de données relationnelles. Une relation peut être vue comme un tableau à 2 dimensions, composé d'un en-tête et d'un corps. Le corps est lui-même composé de t-uplets (lignes) et d'attributs (colonnes). L'en-tête contient les intitulés des attributs, le corps contient les données proprement dites. À noter que l'on emploie aussi le terme "table" à la place de "relation".
CREATE TABLE livres (
id INTEGER PRIMARY KEY,
titre TEXT,
auteur TEXT,
ann_publi INTEGER,
note INTEGER
)INSERT INTO livres (id, titre, auteur, ann_publi, note)
VALUES
(1, '1984', 'Orwell', 1949, 10),
(2, 'Dune', 'Herbert', 1965, 8),
(3, 'Fondation', 'Asimov', 1951, 9),
(4, 'Le meilleur des mondes', 'Huxley', 1931, 7),
(5, 'Fahrenheit 451', 'Bradbury', 1953, 7),
(6, 'Ubik', 'K.Dick', 1969, 9),
(7, 'Chroniques martiennes', 'Bradbury', 1950, 8),
(8, 'La nuit des temps', 'Barjavel', 1968, 7),
(9, 'Blade Runner', 'K.Dick', 1968, 8),
(10, 'Les Robots', 'Asimov', 1950, 9),
(11, 'La Planète des singes', 'Boulle', 1963, 8),
(12, 'Ravage', 'Barjavel', 1943, 8),
(13, 'Le Maître du Haut Château', 'K.Dick', 1962, 8),
(14, 'Le monde des Ā', 'Van Vogt', 1945, 7),
(15, 'La Fin de l’éternité', 'Asimov', 1955, 8),
(16, 'De la Terre à la Lune', 'Verne', 1865, 10)SELECT * FROM livresSe rappeler :
Relation :
Dans le contexte d'une base de données relationnelle, une relation est essentiellement une table qui stocke des données. Elle est composée d'un ensemble de tuples (lignes) ayant des attributs (colonnes) définis.
Attribut :
Un attribut est une propriété ou une caractéristique d'une entité, et il est représenté par une colonne dans une table. Par exemple, pour une table "Personne", "nom" et "prénom" pourraient être des attributs.
3) Domaine
Pour chaque attribut d'une relation, il est nécessaire de définir un domaine : Le domaine d'un attribut donné correspond à un ensemble fini ou infini de valeurs admissibles. Par exemple, le domaine de l'attribut "id" correspond à l'ensemble des entiers (noté INT) : la colonne "id" devra obligatoirement contenir des entiers. Autre exemple, le domaine de l'attribut "titre" correspond à l'ensemble des chaînes de caractères (noté TEXT). Dernier exemple, le domaine de l'attribut "note" correspond à l'ensemble des entiers positifs.
Au moment de la création d'une relation, il est nécessaire de renseigner le domaine de chaque attribut(voir ci-dessus). Le SGBD s'assure qu'un élément ajouté à une relation respecte bien le domaine de l'attribut correspondant : si par exemple vous essayez d'ajouter une note non entière (par exemple 8.5), le SGBD signalera cette erreur et n'autorisera pas l'écriture de cette nouvelle donnée.
4) Clef primaire
Autre contrainte très importante dans les bases de données relationnelles, une relation ou table ne peut pas contenir 2 t-uplets identiques. C'est-à-dire 2 lignes identiques.
Afin d'être sûr de respecter cette contrainte des t-uplets identiques, on définit la notion de "clef primaire".
Une clef primaire est un attribut dont la valeur permet d'identifier de manière unique un t-uplet de la relation. Autrement dit, si un attribut est considéré comme clé primaire, on ne doit pas trouver dans toute la relation 2 fois la même valeur pour cet attribut.
Si on se réfère à l'exemple de la relation ci-dessous :
SELECT * FROM livresL'attribut "note" peut-il jouer le rôle de clé primaire ? Non, car il est possible de trouver 2 fois la même note.
L'attribut "ann_publi" peut-il jouer le rôle de clé primaire ? Non, car il est possible de trouver 2 fois la même année.
L'attribut "auteur" peut-il jouer le rôle de clé primaire ? Non, car il est possible de trouver 2 fois le même auteur.
L'attribut "titre" peut-il jouer le rôle de clé primaire ? A priori oui, car l'attribut "titre" ne comporte pas 2 fois le même titre de roman. Mais, ce n'est pas forcément une bonne idée, car il est tout à fait possible d'avoir un même titre pour 2 romans différents.
Il nous reste donc l'attribut "id". En fait, l'attribut "id" ("id" comme "identifiant") a été placé là pour jouer le rôle de clé primaire. En effet, à chaque fois qu'un roman est ajouté à la relation, son "id" correspond à l'incrémentation de l'id (id du nouveau=id de l'ancien+1) du roman précédemment ajouté. Il est donc impossible d'avoir deux romans avec le même id. Ajouter un attribut "id" afin qu'il puisse jouer le rôle de clé primaire est une pratique courante (mais non obligatoire) dans les bases de données relationnelles. Dans le cas précis qui nous intéresse, il aurait été possible de ne pas utiliser d'attribut "id", car chaque livre édité possède un numéro qui lui est propre : l'ISBN, cet ISBN aurait donc pu jouer le rôle de clé primaire.
À noter qu'en toute rigueur, une clé primaire peut être constituée de plusieurs attributs, par exemple le couple "auteur" + "titre" pourrait jouer le rôle de clé primaire (à moins qu'un auteur écrive 2 romans différents, mais portant tous les deux le même titre), mais nous n'étudierons pas cet aspect des choses ici.
Se rappeler :
clef primaire :
Une clef primaire est un attribut dont la valeur permet d'identifier de manière unique un t-uplet de la relation. Autrement dit, si un attribut est considéré comme clé primaire, on ne doit pas trouver dans toute la relation 2 fois la même valeur pour cet attribut.
5) clef étrangère
a) Duplication des données
Supprimons la relation livres, et créons une plus complète.
DROP TABLE livres; CREATE TABLE livres (
id INT PRIMARY KEY,
titre VARCHAR(255),
nom_auteur VARCHAR(255),
prenom_auteur VARCHAR(255),
date_nai_auteur INT,
langue_ecriture_auteur VARCHAR(255),
ann_publi INT,
note INT
);
INSERT INTO livres (id, titre, nom_auteur, prenom_auteur, date_nai_auteur, langue_ecriture_auteur, ann_publi, note)
VALUES
(1, '1984', 'Orwell', 'George', 1903, 'anglais', 1949, 10),
(2, 'Dune', 'Herbert', 'Frank', 1920, 'anglais', 1965, 8),
(3, 'Fondation', 'Asimov', 'Isaac', 1920, 'anglais', 1951, 9),
(4, 'Le meilleur des mondes', 'Huxley', 'Aldous', 1894, 'anglais', 1931, 7),
(5, 'Fahrenheit 451', 'Bradbury', 'Ray', 1920, 'anglais', 1953, 7),
(6, 'Ubik', 'K.Dick', 'Philip', 1928, 'anglais', 1969, 9),
(7, 'Chroniques martiennes', 'Bradbury', 'Ray', 1920, 'anglais', 1950, 8),
(8, 'La nuit des temps', 'Barjavel', 'René', 1911, 'français', 1968, 7),
(9, 'Blade Runner', 'K.Dick', 'Philip', 1928, 'anglais', 1968, 8),
(10, 'Les Robots', 'Asimov', 'Isaac', 1920, 'anglais', 1950, 9),
(11, 'La Planète des singes', 'Boulle', 'Pierre', 1912, 'français', 1963, 8),
(12, 'Ravage', 'Barjavel', 'René', 1911, 'français', 1943, 8),
(13, 'Le Maître du Haut Château', 'K.Dick', 'Philip', 1928, 'anglais', 1962, 8),
(14, 'Le monde des Ā', 'Van Vogt', 'Alfred Elton', 1912, 'anglais', 1945, 7),
(15, 'La Fin de l’éternité', 'Asimov', 'Isaac', 1920, 'anglais', 1955, 8),
(16, 'De la Terre à la Lune', 'Verne', 'Jules', 1828, 'français', 1865, 10);
SELECT * FROM livresNous avons un peu enrichir la relation LIVRES en ajoutant des informations supplémentaires sur les auteurs. Nous avons ajouté 3 attributs ("prenom_auteur", "date_nai_auteur" et "langue_ecriture_auteur"). Nous avons aussi renommé l'attribut "auteur" en "nom_auteur".
Comme vous l'avez peut-être remarqué, il y a pas mal d'informations dupliquées, par exemple, on retrouve 3 fois "K.Dick Philip 1928 anglais", même chose pour "Asimov Isaac 1920 anglais"...Cette duplication est-elle indispensable ? Non ! Est-elle souhaitable ? Non plus ! En effet, dans une base de données, on évite autant que possible de dupliquer l'information (sauf à des fins de sauvegarde, mais ici c'est toute autre chose). Si nous dupliquons autant de données inutilement c'est que notre structure ne doit pas être la bonne ! Mais alors, comment faire pour avoir aussi des informations sur les auteurs des livres ?
b) Notion de clé étrangère
La solution est relativement simple : travailler avec 2 relations au lieu d'une seule et créer un "lien" entre ces 2 relations :
CREATE TABLE AUTEURS (
id INT PRIMARY KEY,
nom VARCHAR(255),
prenom VARCHAR(255),
ann_naissance INT,
langue_ecriture VARCHAR(255)
);INSERT INTO AUTEURS (id, nom, prenom, ann_naissance, langue_ecriture)
VALUES
(1, 'Orwell', 'George', 1903, 'anglais'),
(2, 'Herbert', 'Frank', 1920, 'anglais'),
(3, 'Asimov', 'Isaac', 1920, 'anglais'),
(4, 'Huxley', 'Aldous', 1894, 'anglais'),
(5, 'Bradbury', 'Ray', 1920, 'anglais'),
(6, 'K.Dick', 'Philip', 1928, 'anglais'),
(7, 'Barjavel', 'René', 1911, 'français'),
(8, 'Boulle', 'Pierre', 1912, 'français'),
(9, 'Van Vogt', 'Alfred Elton', 1912, 'anglais'),
(10, 'Verne', 'Jules', 1828, 'français');
SELECT * FROM AUTEURSSupprimons la relation livres
DROP TABLE livres; Créons une nouvelle relation LIVRES en remplacé l'attribut "auteur" par un attribut "id_auteur".
CREATE TABLE livres (
id INT PRIMARY KEY,
titre VARCHAR(255),
id_auteur INT,
ann_publi INT,
note INT,
FOREIGN KEY (id_auteur) REFERENCES AUTEURS(id)
);
INSERT INTO livres (id, titre, id_auteur, ann_publi, note)
VALUES
(1, '1984', 1, 1949, 10),
(2, 'Dune', 2, 1965, 8),
(3, 'Fondation', 3, 1951, 9),
(4, 'Le meilleur des mondes', 4, 1931, 7),
(5, 'Fahrenheit 451', 5, 1953, 7),
(6, 'Ubik', 6, 1969, 9),
(7, 'Chroniques martiennes', 5, 1950, 8),
(8, 'La nuit des temps', 7, 1968, 7),
(9, 'Blade Runner', 6, 1968, 8),
(10, 'Les Robots', 3, 1950, 9),
(11, 'La Planète des singes', 8, 1963, 8),
(12, 'Ravage', 7, 1943, 8),
(13, 'Le Maître du Haut Château', 6, 1962, 8),
(14, 'Le monde des Ā', 9, 1945, 7),
(15, 'La Fin de l’éternité', 3, 1955, 8),
(16, 'De la Terre à la Lune', 10, 1865, 10);
SELECT * FROM livresSELECT * FROM AUTEURSNous avons créé une relation AUTEURS et nous avons modifié la relation livres : nous avons remplacé l'attribut "auteur" par un attribut "id_auteur".
Comme vous l'avez sans doute remarqué, l'attribut "id_auteur" de la relation LIVRES permet de créer un lien avec la relation AUTEURS. "id_auteur" correspond à l'attribut "id" de la relation AUTEURS. L'introduction d'une relation AUTEURS et la mise en place de liens entre cette relation et la relation LIVRES permettent d'éviter la {redondance d'informations.
Pour établir un lien entre 2 relations livres et AUTEURS, on ajoute à livres un attribut x qui prendra les valeurs de la clé primaire de AUTEURS. Cet attribut x est appelé clef étrangère (l'attribut correspond à la clef primaire d'une autre table, d'où le nom).
Dans l'exemple ci-dessus, l'attribut "id_auteur" de la relation LIVRES permet bien d'établir un lien entre la relation livres et la relation AUTEURS, "id_auteur" correspond bien à la clé primaire de la relation AUTEURS,
conclusion : "id_auteur" est une clef étrangère.
Pour préserver l'intégrité d'une base de données, il est important de bien vérifier que toutes les valeurs de la clé étrangère correspondent bien à des valeurs présentes dans la clé primaire (nous aurions un problème d'intégrité de la base de données si une valeur de l'attribut "id_auteur" de la relation LIVRES ne correspondait à aucune valeur de la clé primaire de la relation AUTEURS). Certains SGBD ne vérifient pas cette contrainte (ne renvoient aucune erreur en cas de problème), ce qui peut provoquer des comportements erratiques.
6) schéma relationnel
Dernière définition, on appelle schéma relationnel l'ensemble des relations présentes dans une base de données. Quand on vous demande le schéma relationnel d'une base de données, il est nécessaire de fournir les informations suivantes :
- Les noms des différentes relations
- pour chaque relation, la liste des attributs avec leur domaine respectif
- pour chaque relation, la clé primaire et éventuellement les clés étrangères
Voici un exemple pour les relations LIVRES et AUTEURS :
AUTEURS(id : INT, nom : TEXT, prenom : TEXT, ann_naissance : INT, langue_ecriture : TEXT)
LIVRES(id : INT, titre : TEXT, #id_auteur : INT, ann_publi : INT, note : INT)
Les attributs soulignés sont des clés primaires, le # signifie que l'on a une clé étrangère.
2.2 - SQL Requêtes ✔
NSI - Terminale - Bases de données
Langage SQL : requêtes d’interrogation et de mise à jour d’une base de données
Capacités attendues :
- Identifier les composants d’une requête.
- Construire des requêtes d’interrogation à l’aide des clauses du langage SQL: SELECT, FROM, WHERE, JOIN.
- Construire des requêtes d’insertion et de mise à jour à l’aide de : UPDATE, INSERT, DELETE
Commentaires :
On peut utiliser DISTINCT, ORDER BY ou les fonctions d’agrégation sans utiliser les clauses GROUP BY et HAVING.
Entrainement
- BAC 2023 EX 1 SQL Sujet 12
- BAC 2023 EX 3 SQL Sujet 10
- BAC 2023 EX 3 SQL Sujet 9
1) introduction
Nous avons eu l'occasion d'étudier la structure d'une base de données relationnelle, nous allons maintenant apprendre à réaliser des requêtes, c'est-à-dire que nous allons apprendre à créer une base des données, créer des attributs, ajouter de données, modifier des données et enfin, nous allons surtout apprendre à interroger une base de données afin d'obtenir des informations.
Pour réaliser toutes ces requêtes, nous allons devoir apprendre un langage de requêtes : SQL (Structured Query Language). SQL est propre aux bases de données relationnelles, les autres types de bases de données utilisent d'autres langages pour effectuer des requêtes.
Dans ce cours nous allons travailler avec SQLite. SQLite est un système de gestion de base de données relationnelle très répandu. Noter qu'il existe d'autres systèmes de gestion de base de données relationnelle comme MySQL ou PostgreSQL. Dans tous les cas, le langage de requête utilisé est le SQL (même si parfois on peut noter quelques petites différences). Ce qui sera vu ici avec SQLite pourra, à quelques petites modifications près, être utilisé avec, par exemple, MySQL.
CREATE TABLE AUTEURS (
id INT PRIMARY KEY,
nom VARCHAR(255),
prenom VARCHAR(255),
ann_naissance INT,
langue_ecriture VARCHAR(255)
);INSERT INTO AUTEURS (id, nom, prenom, ann_naissance, langue_ecriture)
VALUES
(1, 'Orwell', 'George', 1903, 'anglais'),
(2, 'Herbert', 'Frank', 1920, 'anglais'),
(3, 'Asimov', 'Isaac', 1920, 'anglais'),
(4, 'Huxley', 'Aldous', 1894, 'anglais'),
(5, 'Bradbury', 'Ray', 1920, 'anglais'),
(6, 'K.Dick', 'Philip', 1928, 'anglais'),
(7, 'Barjavel', 'René', 1911, 'français'),
(8, 'Boulle', 'Pierre', 1912, 'français'),
(9, 'Van Vogt', 'Alfred Elton', 1912, 'anglais'),
(10, 'Verne', 'Jules', 1828, 'français');CREATE TABLE LIVRES (
id INT PRIMARY KEY,
titre VARCHAR(255),
id_auteur INT,
ann_publi INT,
note INT,
FOREIGN KEY (id_auteur) REFERENCES AUTEURS(id)
);INSERT INTO LIVRES (id, titre, id_auteur, ann_publi, note)
VALUES
(1, '1984', 1, 1949, 10),
(2, 'Dune', 2, 1965, 8),
(3, 'Fondation', 3, 1951, 9),
(4, 'Le meilleur des mondes', 4, 1931, 7),
(5, 'Fahrenheit 451', 5, 1953, 7),
(6, 'Ubik', 6, 1969, 9),
(7, 'Chroniques martiennes', 5, 1950, 8),
(8, 'La nuit des temps', 7, 1968, 7),
(9, 'Blade Runner', 6, 1968, 8),
(10, 'Les Robots', 3, 1950, 9),
(11, 'La Planète des singes', 8, 1963, 8),
(12, 'Ravage', 7, 1943, 8),
(13, 'Le Maître du Haut Château', 6, 1962, 8),
(14, 'Le monde des Ā', 9, 1945, 7),
(15, 'La Fin de l’éternité', 3, 1955, 8),
(16, 'De la Terre à la Lune', 10, 1865, 10);Nous allons travailler avec les 2 tables (relations) suivantes :AUTEURS et LIVRES
SELECT * FROM AUTEURSSELECT * FROM LIVRES2) Requêtes d'interrogation
a) Requêtes d'interrogation "simples"
Quand on désire extraire des informations d'une table, on effectue une requête d'interrogation à l'aide du mot clé SELECT. Voici un exemple de requête d'interrogation :
SELECT id, titre, id_auteur, ann_publi, note
FROM LIVRESIl est possible d'obtenir uniquement certains attributs. Par exemple :
SELECT nom, prenom
FROM AUTEURSb) sélectionner certaines lignes : la clause WHERE
Il est possible d'utiliser la clause WHERE afin d'imposer une (ou des) condition(s) permettant de sélectionner uniquement certaines lignes.
La condition doit suivre le mot-clé WHERE :
SELECT titre
FROM LIVRES
WHERE note > 9La requête ci-dessus permettra d'afficher uniquement les titres qui ont une note strictement supérieure à 9 (soit "1984" et "De la Terre à la Lune")
Il est possible de combiner les conditions à l'aide d'un OR ou d'un AND :
SELECT nom
FROM AUTEURS
WHERE langue_ecriture = 'français' AND ann_naissance > 1900Il est aussi possible d'utiliser le OR à la place du AND :
SELECT nom
FROM AUTEURS
WHERE langue_ecriture = 'français' OR ann_naissance > 1920c) mettre dans l'ordre les réponses : la clause ORDER BY
Il est possible de classer les résultats d'une requête par ordre croissant grâce à la clause ORDER BY :
SELECT nom, ann_naissance
FROM AUTEURS
WHERE langue_ecriture = 'français' ORDER BY ann_naissanceEn rajoutant DESC, on obtient l'ordre décroissant :
SELECT nom, ann_naissance
FROM AUTEURS
WHERE langue_ecriture = 'français' ORDER BY ann_naissance DESCÀ noter que si la clause ORDER BY porte sur une chaine de caractères, on obtient alors l'ordre alphabétique :
SELECT nom
FROM AUTEURS
WHERE langue_ecriture = 'français' ORDER BY nomd) La clause DISTINCT
Il est possible d'éviter les doublons dans une réponse grâce à la clause DISTINCT. Imaginons la table suivante :
CREATE TABLE MACHINES (
numero INT PRIMARY KEY,
type VARCHAR(10),
proprietaire VARCHAR(50)
);
INSERT INTO MACHINES (numero, type, proprietaire) VALUES
(1, 'X23', 'Marc'),
(2, 'Y43', 'Pierre'),
(3, 'Z24', 'Kevin'),
(4, 'Y44', 'Marc');SELECT * FROM MACHINESSELECT proprietaire
FROM MACHINESPour éviter ce doublon, nous pouvons écrire :
SELECT DISTINCT proprietaire
FROM MACHINESe) Les jointures
Nous avons 2 tables, grâce aux jointures nous allons pouvoir associer ces 2 tables dans une même requête.
En général, les jointures consistent à associer des lignes de 2 tables. Elles permettent d'établir un lien entre 2 tables. Qui dit lien entre 2 tables dit souvent clé étrangère et clé primaire.
Analysons la requête suivante :
SELECT *
FROM LIVRES
INNER JOIN AUTEURS ON LIVRES.id_auteur = AUTEURS.idLe FROM LIVRES INNER JOIN AUTEURS permet de créer une jointure entre les tables LIVRES et AUTEURS ("rassembler" les tables LIVRES et AUTEURS en une seule grande table). Le "ON LIVRES.id_auteur = AUTEURS.id" signifie qu'une ligne quelconque A de la table LIVRES devra être fusionnée avec la ligne B de la table AUTEURS à condition que l'attribut id_auteur de la ligne A soit égal à l'attribut id de la ligne B.
À noter que pour éviter toute confusion il est souvent judicieux d'ajouter le nom de la table juste devant le nom de l'attribut : on écrira AUTEURS.id au lieu de simplement id, en effet, si on écrivait seulement id, il n'y aurait aucun moyen de distinguer l'id de la table LIVRES et l'id de la table AUTEURS. Je vous conseille d'adopter cette écriture systématiquement en cas de jointure, même quand cela n'est pas obligatoire (par exemple on aurait pu écrire id_auteur à la place de LIVRES.id_auteur puisqu'il y a uniquement un id_auteur dans la table LIVRES), cela vous permettra d'éviter certains déboires.
Dans le cas d'une jointure, il est tout à fait possible de sélectionner certains attributs et pas d'autres (aucune obligation de sélectionner tous les attributs des 2 tables :
SELECT LIVRES.titre, AUTEURS.nom, AUTEURS.prenom
FROM AUTEURS
INNER JOIN LIVRES ON LIVRES.id_auteur = AUTEURS.idf) utilisation du WHERE dans les jointures
Suite à une jointure il est possible de sélectionner certaines lignes grâce à la clause WHERE :
SELECT LIVRES.titre,AUTEURS.nom, AUTEURS.prenom
FROM LIVRES
INNER JOIN AUTEURS ON LIVRES.id_auteur = AUTEURS.id
WHERE LIVRES.ann_publi>1965g) Les jointures plus complexes
Pour terminer avec les jointures, vous devez savoir que nous avons abordé la jointure la plus simple (INNER JOIN). Il existe des jointures plus complexes (CROSS JOIN, LEFT JOIN, RIGHT JOIN), ces autres jointures ne seront pas abordées dans ce cours.
3) requêtes d'insertion
Il est possible d'ajouter une entrée à une table grâce à une requête d'insertion :
INSERT INTO LIVRES
(id,titre,id_auteur,ann_publi,note)
VALUES
(17,'Hypérion',11,1989,8);On emploie les mots clés INSERT INTO suivi de la table concernée (ici LIVRES). Ensuite on indique les noms des attributs que l'on désire ajouter (ici (id,titre,auteur,ann_publi,note)), et enfin pour terminer les valeurs de chaque attribut (ici (17,'Hypérion','Simmons',1989,8), attention à bien respecter l'ordre : 17 correspond à id, Hypérion correspond au titre, 11 correspond à id_auteur, 1989 correspond à ann_publi et 8 correspond à note).
4) requêtes de mise à jour
"UPDATE" va permettre de modifier une ou des entrées. Nous utiliserons "WHERE", comme dans le cas d'un "SELECT", pour spécifier les entrées à modifier. Voici un exemple de modification :
UPDATE LIVRES
SET note=10
WHERE titre = 'Dune'Cette requête permet de modifier la note du(des) livre(s) ayant pour titre Dune.
SELECT * FROM LIVRES5) Requêtes de suppression
DELETE est utilisée pour effectuer la suppression d'une (ou de plusieurs) entrée(s). Ici aussi c'est le "WHERE" qui permettra de sélectionner les entrées à supprimer :
DELETE FROM LIVRES
WHERE titre='Dune'SELECT * FROM LIVRESDELETE FROM LIVRES Attention à l'utilisation de cette requête DELETE notamment si on oublie le WHERE. on supprimerait toutes les entrées de la table LIVRES :
SELECT * FROM LIVRESCe qu’il faut savoir
Pour consulter des données, ajouter une entrée, modifier une entrée ou supprimer une entrée dans une base de données relationnelle, il est nécessaire d’effectuer des “requêtes SQL” (utilisation du langage SQL)
Pour ajouter des entrées à une table, on utilisera “INSERT” (exemple : INSERT INTO LIVRES (id,titre,auteur,ann_publi,note) VALUES (1,'1984','Orwell',1949,10);)
Pour interroger une table, on utilisera “SELECT” (exemple : SELECT titre FROM LIVRES WHERE auteur='Asimov')
Pour modifier une entrée, on utilisera “UPDATE” (exemple : UPDATE LIVRES SET note=10 WHERE titre = 'Dune')
Pour supprimer une entrée, on utilisera “DELETE” (exemple : DELETE FROM LIVRES WHERE titre='Dune')
Pour réaliser une jointure, il est possible d’utiliser “INNER JOIN” (exemple : SELECT FROM LIVRES INNER JOIN AUTEURS ON LIVRES.id_auteur = AUTEURS.id)
Exercice :
Un ski-club utilise une base de données constituée de 2 tables :
- une table ADHERENTS
- une table STATIONS
Dans la table ADHERENTS on trouve un attribut “ref_station” qui permet de connaître les stations de ski préférées des adhérents.
Table ADHERENTS
| num_licence | nom | prenom | annee_naissance | ref_station |
|---|---|---|---|---|
| 12558 | Doe | John | 1988 | 5 |
| 13668 | Vect | Alice | 1974 | 6 |
| 1777 | Dect | Bob | 1967 | 3 |
| 13447 | Beau | Tristan | 1999 | 4 |
| 1141 | Pabeau | John | 1975 | 3 |
table STATIONS
| ref | nom | altitude_max |
|---|---|---|
| 3 | Le grand Bornand | 2050 |
| 4 | La clusaz | 2616 |
| 5 | Flaine | 2510 |
| 6 | Avoriaz | 2466 |
- Comment appelle-t-on l’attribut ref_station de la table ADHERENTS ?
- Écrire la requête SQL permettant d’obtenir le nom des stations ayant une altitude maxi strictement supérieure à 2500 m.
- Écrire une requête SQL permettant d’obtenir le numéro de licence des adhérents nés après 1980 et ayant pour prénom John.
- Donnez le résultat de la requête SQL suivante :
Réponse :
- L'attribut "ref_station" de la table ADHERENTS est appelé une "clé étrangère" (ou Foreign Key en anglais).
- SELECT nom FROM STATIONS WHERE altitude_max > 2500;
- ELECT num_licence FROM ADHERENTS WHERE annee_naissance > 1980 AND prenom = 'John';
- Doe, Vect, Beau
- Flaine, Avoriaz
3.1 - Système sur puce
Architectures matérielles, systèmes d’exploitation et réseaux
Composants intégrés d’un système sur puce
Capacités Attendue :
Identifier les principaux composants sur un schéma de circuit et les avantages de leur intégration en termes de vitesse et de consommation.
Commentaires :
Le circuit d’un téléphone peut être pris comme un exemple : microprocesseurs, mémoires locales, interfaces radio et filaires, gestion d’énergie, contrôleurs vidéo, accélérateur graphique, réseaux sur puce, etc.
1. Loi de Moore et miniaturisation progressive
1.1 La Loi de Moore

La loi de Moore, énoncée pour la première fois en 1965 par Gordon Moore, co-fondateur d'Intel, a prédit avec une précision remarquable la croissance exponentielle de la densité des transistors sur les puces électroniques pendant plusieurs décennies.
Cette progression fulgurante a été rendue possible grâce à des avancées constantes dans la technologie de fabrication, permettant une miniaturisation progressive des composants, et à des découvertes cruciales en physique des semi-conducteurs, qui ont optimisé la performance et la fiabilité des transistors à des échelles toujours plus réduites.
Cependant, après des décennies de croissance soutenue, nous observons aujourd'hui des signes indiquant un ralentissement de cette tendance. Les contraintes physiques, telles que les effets quantiques qui deviennent prédominants à de très petites échelles, ainsi que les défis économiques liés au coût croissant de la fabrication à l'échelle nanométrique, semblent indiquer que la loi de Moore pourrait ne pas être soutenable indéfiniment.
Alors que l'industrie des semi-conducteurs recherche des solutions innovantes pour surmonter ces obstacles, il est de plus en plus évident que la poursuite de la miniaturisation à tout prix n'est plus le seul paradigme dirigeant l'évolution des technologies informatiques.
import numpy as np
import matplotlib.pyplot as plt
# Données approximatives prises à partir du graphique
data = [
(1971, 2300, 'Intel 4004'),
(1972, 3500, 'Intel 8008'),
(1974, 6000, 'Intel 8080'),
(1978, 29000, 'Intel 8086'),
(1982, 120000, 'Intel 80286'),
(1985, 275000, 'Intel 80386'),
(1989, 1200000, 'Intel 80486'),
(1993, 3100000, 'Pentium'),
(1995, 5500000, 'Pentium Pro'),
(1997, 7500000, 'Pentium II'),
(1999, 24000000, 'Pentium III'),
(2002, 55000000, 'Pentium 4'),
(2004, 110000000, 'Pentium M'),
(2006, 291000000, 'Core 2 Duo'),
(2008, 2300000000, 'Core i7'),
(2010, 3000000000, 'Westmere i7'),
(2012, 5000000000, 'Ivy Bridge i7'),
(2014, 1400000000, 'Broadwell i7'),
(2016, 3200000000, 'Kaby Lake i7'),
(2018, 10000000000, 'AMD Ryzen'),
(2020, 40000000000, 'Recent Chip'),
]
years, transistors, labels = zip(*data)
plt.figure(figsize=(14, 8))
plt.yscale("log")
plt.scatter(years, transistors, color='blue')
for i, txt in enumerate(labels):
plt.annotate(txt, (years[i], transistors[i]), fontsize=8, ha='right')
# Tracer la courbe de la multiplication par 2 des transistors tous les 2 ans
start_year = 1971
start_transistors = 2300
trend_years = list(np.arange(start_year, 2023, 2))
trend_transistors = [start_transistors * (2 ** ((year - start_year) / 2)) for year in trend_years]
plt.plot(trend_years, trend_transistors, color='red', linestyle='--', label="Tendance x2 tous les 2 ans")
plt.title("Loi de Moore: Évolution du nombre de transistors")
plt.xlabel("Année")
plt.ylabel("Nombre de transistors (échelle log)")
plt.grid(True, which="both", ls="--", c='0.7')
plt.legend()
plt.show()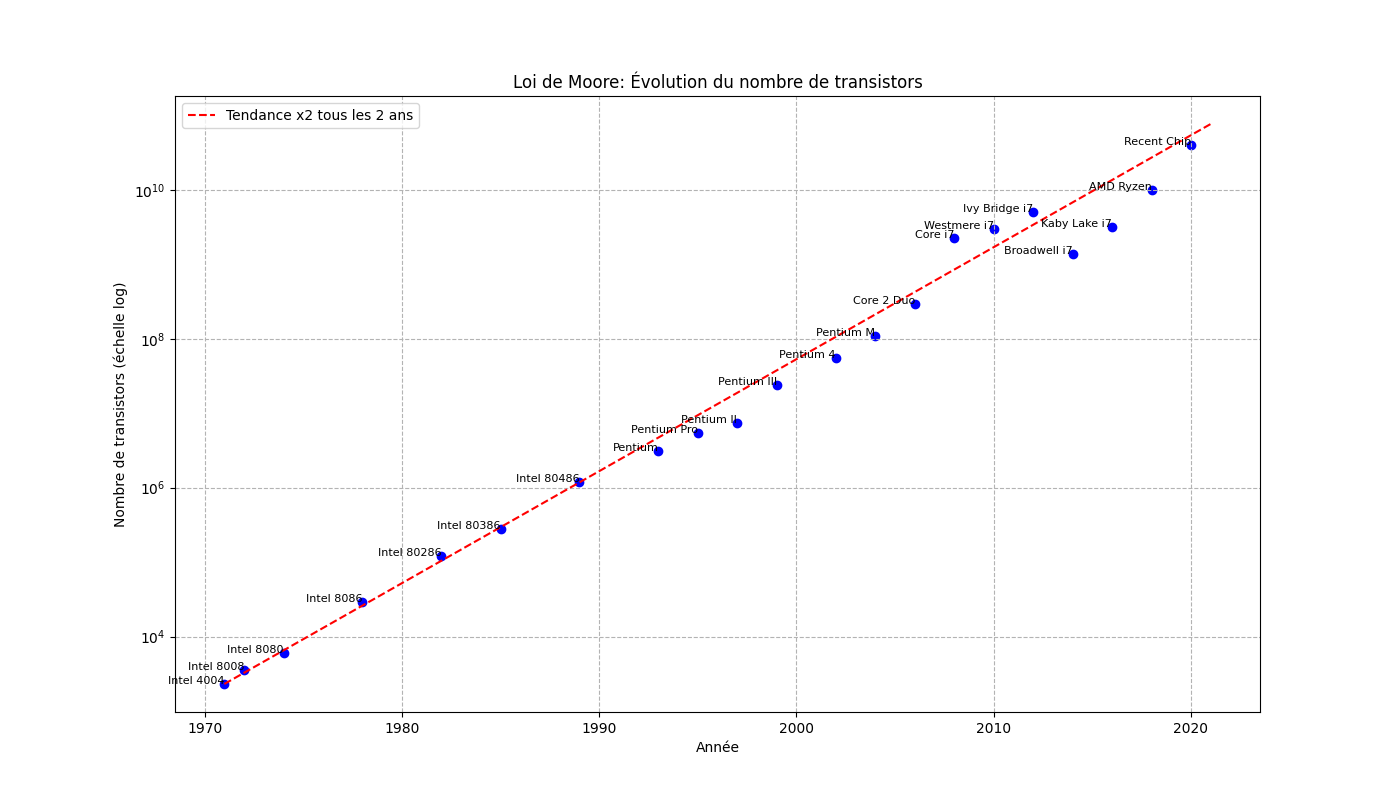
Graphique semi-logarithmique du nombre de transistors
pour les microprocesseurs par rapport aux dates d'introduction1.2 Évolution de la taille des ordinateurs
1.2.1 IBM 650, le premier ordinateur fabriqué en série (1955)

Cet ordinateur n'a pas encore de transistors mais des tubes à vide.1.2.2 IBM 7090, le premier ordinateur à transistors (1959)

Le transistor permet de laisser passer ou ne pas laisser passer un courant électrique1.2.3 Le rôle crucial de la taille des transistors
Ainsi que l'avait prédit Moore, c'est la progression du nombre de transistors gravables sur le processeur qui guidera pendant des années l'évolution de l'informatique :
2. Composition d'un pc actuel
- CPU / Fan & Heatsink : Le CPU (Central Processing Unit) est le cerveau de l'ordinateur.
Le ventilateur (Fan) et le radiateur (Heatsink) sont utilisés pour refroidir le CPU.
- RAM : La RAM (Random Access Memory) est la mémoire vive de l'ordinateur.
- Optical Drive Bays : emplacements pour lecteurs DVD ou Blu-ray.
- GPU : Le GPU (Graphics Processing Unit) est responsable du rendu graphique.
- Expansion Slots : emplacements sur la carte mère pour ajouter des cartes d'extension comme une carte son ou réseau.
- Hard Drive : stockage de données de l'ordinateur : système d'exploitation, applications et données personnelles.
- SSD : Le SSD (Solid State Drive) est une autre forme de stockage, similaire au disque dur, mais en mémoire flash au lieu des disques rotatifs, ce qui le rend plus rapide et moins sujet aux pannes mécaniques.
- Power Supply : L'alimentation fournit de l'électricité à tous les composants de l'ordinateur.
- Motherboard : La carte mère est le composant principal qui relie tous les autres composants entre eux. Chaque composant a un rôle spécifique. Ils communiquent entre eux par des bus de différentes vitesses.
Chaque composant est remplaçable, et il est possible d'ajouter de nouveaux composants sur la carte mère qui possède des slots d'extension.
3. Tout un pc sur une seule puce : les SoC
Le principe d'un système sur puce ou System On a Chip (SoC) est d'intégrer au sein d'une puce unique un ensemble de composants habituellement physiquement dissociés dans un ordinateur classique (ordinateur de bureau ou ordinateur portable).
On peut retrouver ainsi au sein d'une même puce :
- le microprocesseur (CPU)
- la carte graphique (GPU)
- la mémoire RAM
- éventuellement des composants de communication (WiFi, Bluetooth...)
✅ Avantages d'un SoC
- moindre consommation électrique
- moindre encombrement
- pas besoin de refroidissement
- meilleure sécurité (vue globale sur la sécurité qui n'est plus dépendante d'une multitude de composants)
- moindre coût (forte automisation du processus, gros volumes de production)
📛 Inconvénients
- Impossibilité de choisir indépendamment ses composants
- Pas de mise à jour possible / remplacement / ajout d'un composant
- La panne d'un seul composant entraîne la panne totale du SoC
Exemple : A15 Bionic

A15 Bionic, qui équipe les iPhone 13. Cette puce est fabriquée par TSMC.
Cette puce contient :
- 15 milliards de transistors (gravés à 5 nm)
- un processeur central à 6 cœurs (2 cœurs hautes performances + 4 cœurs plus économes en énergie)
- un GPU (processeur dédié uniquement au calcul du rendu graphique) de 5 cœurs.
- une puce dédiée au Machine Learning (Neural Engine)L'intégration dans un SoC n'est pas totale : il reste des puces dédiées à des tâches très spécifiques qui ne sont pas forcément intégrées dans le SoC.
Ainsi, d'après le site iFixit, on peut retrouver ceci dans l'iPhone Pro 13, au côté de la puce A15 évoquée plus haut :

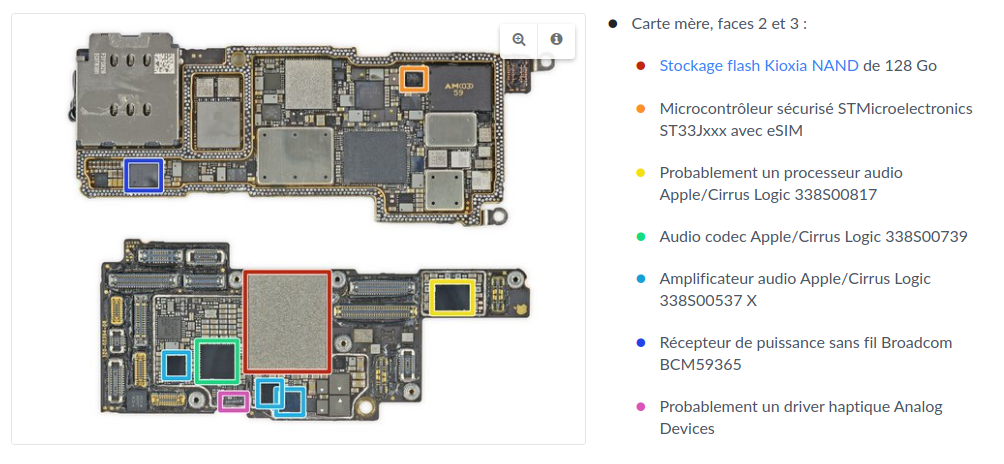
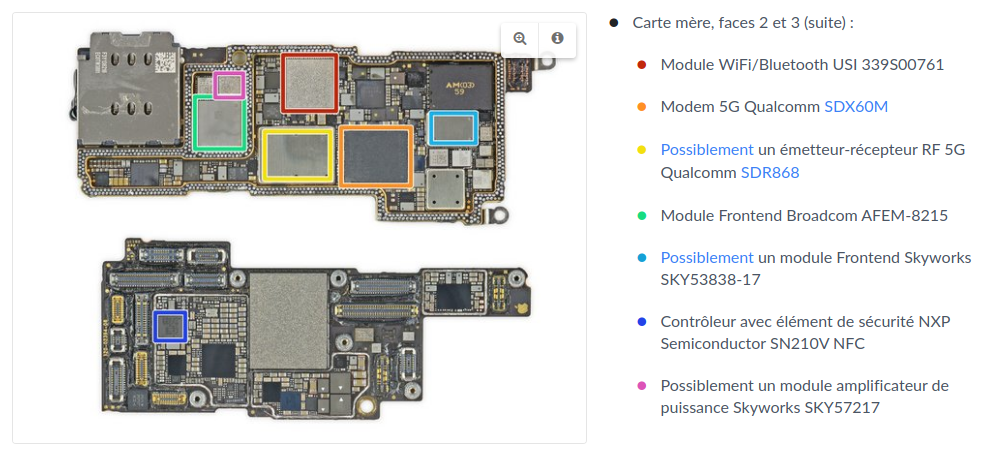
On voit que (par exemple) qu'il existe :
- une puce spécifique pour gérer l'audio,
- une puce spécifique pour le module WiFi,
- une puce spécifique pour le module Modem 5G...4. Electronique «grand public»

Les cartes Arduino sont constituées d'un microcontrôleur et d'un certain nombre d'entrées/sorties numériques et analogiques.
Ces entrées/sorties permettent à la carte de se connecter à divers composants tels que des LED, des capteurs, des moteurs, etc.
Arduino est couramment utilisé pour une variété de projets allant des simples bricolages aux prototypes complexes pour les produits finis. Que ce soit pour automatiser une plante d'intérieur, construire un robot, ou créer une station météo, Arduino est une excellente option pour les débutants et les experts en électronique.
source : glassus

3.2 - Processus, système
Architectures matérielles, systèmes d’exploitation et réseaux
Gestion des processus et des ressources par un système d’exploitation.
Capacités Attendue :
- Décrire la création d’un processus, l’ordonnancement de plusieurs processus par le système.
- Mettre en évidence le risque de l’interblocage (deadlock).
Commentaires :
- À l’aide d’outils standard, il s’agit d’observer les processus actifs ou en attente sur une machine.
- Une présentation débranchée de l’interblocage peut être proposée.
1. Notion de processus
1.1 Définition d'un processus
Lorsqu'un programme est exécuté sur un ordinateur, celui-ci va créer un ou plusieurs processus.
On dit que ce processus est une instance d'exécution de ce programme.
Un processus est caractérisé par :
- l'ensemble des instructions qu'il va devoir accomplir
- les ressources que le programme va mobiliser
- l'état des registres du processeur
1.2 Observation des processus.
Windows fournit plusieurs outils pour observer et gérer les processus :
-
Gestionnaire des tâches:
Vous pouvez y accéder en appuyant simultanément sur les touches Ctrl + Shift + Esc ou Ctrl + Alt + Suppr, et en choisissant "Gestionnaire des tâches". Cet outil graphique affiche une liste : - des processus en cours d'exécution, - leur utilisation du CPU, de la mémoire, du disque et du réseau.
-
Commande tasklist:
Ouvrez l'invite de commandes (cmd) et tapez tasklist. Cette commande affiche une liste des processus en cours avec leur identifiant de processus (PID).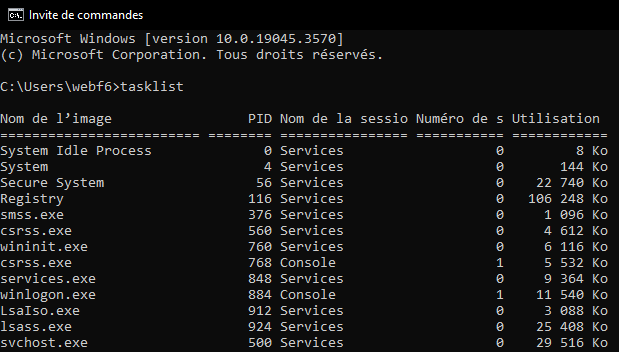
-
PowerShell:
Ouvrez PowerShell et utilisez la commande Get-Process.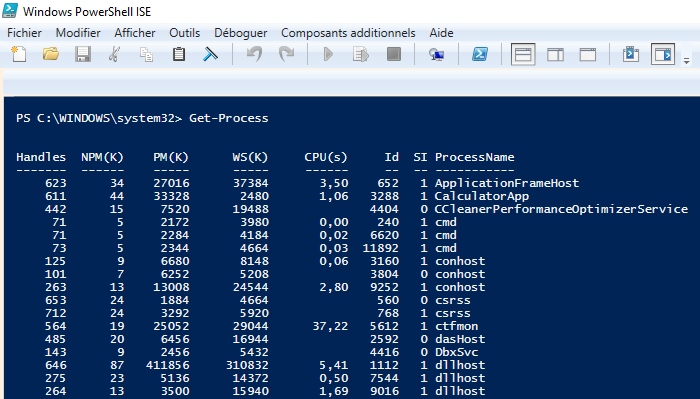
Pour obtenir des détails sur les processus d'un utilisateur spécifique, cela pourrait être un peu plus complexe car Windows ne stocke pas l'information de l'utilisateur directement avec le processus. Mais vous pouvez utiliser des scripts ou des modules supplémentaires pour obtenir ces informations. Exemple dans PowerShell: Get-WmiObject win32_process | Select-Object Name, ProcessId, ParentProcessId

Pour comprendre la correspondance entre PID et PPID:
- PID (ProcessId) : Il s'agit de l'identifiant unique du processus.
Chaque processus sur votre système d'exploitation a un PID distinct.
-PPID (ParentProcessId) : Il s'agit de l'identifiant du processus parent qui a lancé le processus actuel.
Si un processus n'a pas de processus parent, cette valeur peut être 0.- Outils tiers:
Il existe plusieurs outils tiers qui peuvent vous donner une vue détaillée des processus en cours d'exécution similaires
Sous Linux , on peux utilise la commade ps.
Un exemple populaire est Sysinternals Process Explorer
.
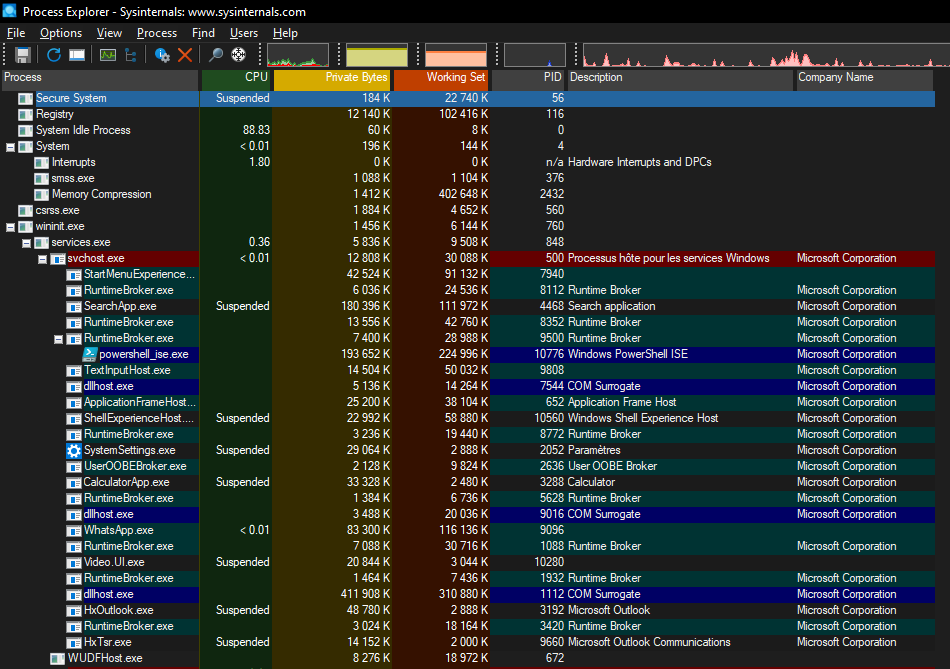
2. Ordonnancement
L'ordonnancement est le mécanisme par lequel un système d'exploitation décide quel processus en attente doit être alloué au processeur pour son exécution. L'ordonnancement vise à optimiser certaines propriétés du système, comme le temps de réponse, le débit ou l'utilisation du processeur.
Un ordinateur semble effectuer plusieurs opérations en même temps. Cependant, à moins que le processeur ne possède de multiples cœurs, ce n'est pas le cas.
Le système d'exploitation lance ces processus de manière séquentielle. Malgré cela, il semble qu'ils soient tous « actifs simultanément » : c'est ce qu'on appelle la programmation concurrente.
Même si ces processus existent durant la même période, ils fonctionnent successivement. Le processeur ne peut gérer qu'un processus à la fois.
Leur exécution à un rythme très soutenu donne l'impression d'une simultanéité, bien qu'elle soit illusoire.
Explorons cette notion plus en détail, considérons les scripts progA et progB ci-dessous :
Temps 2 machines.py :
import threading
import time
def progA():
for i in range(10):
current_time_ns = time.time_ns()
print(f"[{current_time_ns}] programme A en cours, itération {i}")
time.sleep(0.1)
def progB():
for i in range(10):
current_time_ns = time.time_ns()
print(f"[{current_time_ns}] programme B en cours, itération {i}")
time.sleep(0.1)
# Création de deux threads distincts pour exécuter les fonctions progA et progB.
t1 = threading.Thread(target=progA)
t2 = threading.Thread(target=progB)
# Démarrage des deux threads, leur permettant d'exécuter les fonctions en parallèle
t1.start()
t2.start()
# Attente que les deux threads aient terminé avant de poursuivre
t1.join()
t2.join()Python 3.11.3
[1698169303153550200] programme A en cours, itération 0
[1698169303153550200] programme B en cours, itération 0
[1698169303255943600] programme A en cours, itération 1
[1698169303256450900] programme B en cours, itération 1
[1698169303356815500] programme A en cours, itération 2
[1698169303356815500] programme B en cours, itération 2
[1698169303457698400] programme A en cours, itération 3
[1698169303457698400] programme B en cours, itération 3
[1698169303558466200] programme A en cours, itération 4
[1698169303558466200] programme B en cours, itération 4
[1698169303659003900] programme A en cours, itération 5
[1698169303659003900] programme B en cours, itération 5
[1698169303759853300] programme A en cours, itération 6
[1698169303759853300] programme B en cours, itération 6
[1698169303860672100] programme A en cours, itération 7
[1698169303860672100] programme B en cours, itération 7
[1698169303960965400] programme A en cours, itération 8
[1698169303960965400] programme B en cours, itération 8
[1698169304061331000] programme B en cours, itération 9
[1698169304061331000] programme A en cours, itération 9 Il en résulte un mauvais entrelacement entre les phrases progA en cours et progB en cours. Mais si l'on regarde les temps, ce n'est qu'un problème d'affichage car les programmes sont simultanées.
Pour mettre en évidence, l'alternance entre les divers processus, il faut augmenter le nombres de processueur pour dépasser le nombre de coeurs.
Temps n machines.py
import threading
import time
# Déterminer le nombre de programmes (threads) à exécuter
num_programs = int(input("Combien de programmes souhaitez-vous exécuter ? "))
# Initialiser le tableau pour stocker les temps pour chaque programme et chaque itération
time_table = [[0 for _ in range(num_programs)] for _ in range(10)]
# Pour stocker le temps minimum pour chaque itération
min_times = [float('inf') for _ in range(10)]
# Capturer le temps de départ en nanosecondes
start_time_ns = time.time_ns()
def prog(num):
for i in range(10):
current_time_ns = time.time_ns()
elapsed_time_ns = current_time_ns - start_time_ns
time_table[i][num] = elapsed_time_ns
min_times[i] = min(min_times[i], elapsed_time_ns) # Mettre à jour le temps minimum
# print(f"[{elapsed_time_ns:20}] programme {num:2} en cours, itération {i}")
time.sleep(0.1)
# Création des threads pour exécuter les fonctions prog
threads = []
for i in range(num_programs):
t = threading.Thread(target=prog, args=(i,))
threads.append(t)
t.start()
# Attente que tous les threads aient terminé avant de poursuivre
for t in threads:
t.join()
# Affichage des données sous forme de tableau
print("\nTableau des temps écoulés depuis le début et des différences de temps:")
header_format = "{:<8}{:<20}"
column_format = "{:<12}"
print(header_format.format('Étape', 'Min Temps'), end="")
for i in range(num_programs):
print(column_format.format(f"Prog {i}"), end="")
print()
for i in range(10):
print(header_format.format(i, min_times[i]), end="")
for j in range(num_programs):
diff = time_table[i][j] - min_times[i] # Calculer la différence par rapport au temps minimum
print(column_format.format(diff), end="")
print()
Python 3.11.3
Combien de programmes souhaitez-vous exécuter ? 5
Tableau des temps écoulés depuis le début et des différences de temps:
Étape Min Temps Prog 0 Prog 1 Prog 2 Prog 3 Prog 4
0 0 0 0 0 0 0
1 109463600 0 0 1070200 1070200 2084700
2 210114300 0 0 1030900 1030900 2039100
3 310738400 0 0 605900 605900 1661500
4 410977700 0 531500 1056900 531500 1565500
5 511877900 0 0 574700 0 1348700
6 612419900 0 0 544100 0 1560500
7 713313600 0 0 0 0 1262500
8 813911100 0 557900 0 557900 1187700
9 914628600 0 0 0 555900 1061200L'affichage durant l'exécution peut-être une source de ralentissement, je l'ai supprimée. Et là, enfin nous voyons de l'alternance.
Si la gestion des processus était réellement simultanée, même en considérant des ralentissements du processeur par des sollicitations extérieures, chaque processus serait ralenti de la même manière : l'entrelacement des phrases serait toujours le même.
En réalité, le processeur passe son temps à alterner entre les divers processus qu'il a à gérer, et les met en attente quand il ne peut pas s'occuper d'eux. Il obéit pour cela aux instructions de son ordonnanceur.
Différents types d'ordonnancement :
Si on vous donne 4 tâches A, B, C et D à accomplir, vous pouvez décider :
- de faire la tâche prioritaire d'abord ;
- de faire la tâche la plus rapide d'abord ;
- de faire la tâche la plus longue d'abord ;
- de les faire dans l'ordre où elles vous ont été données ;
- de faire à tour de rôle chaque tâche pendant un temps fixe jusqu'à ce qu'elles soient toutes terminées ... ...
Un processeur est confronté aux mêmes choix : comment déterminer quel processus doit être traité à quel moment ? Le schéma ci-dessous présente quelques politiques d'ordonnancement :
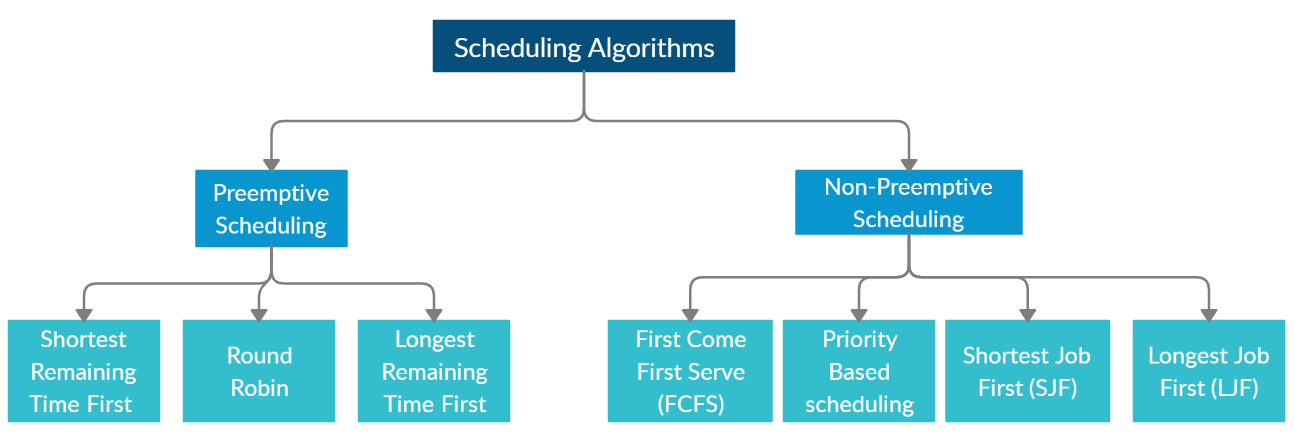
Dans le cas (très fréquent maintenant) d'un processeur multi-cœurs, le problème reste identique. Certes, sur 4 cœurs, 4 processus pourront être traités simultanément (une réelle simultanéité) mais il reste toujours beaucoup plus de processus à traiter que de cœurs dans le processeur... et un ordonnancement est donc toujours nécessaire.
Sous Linux, l'ordonnancement est effectué par un système hybride où les processus sont exécutés à tour de rôle (on parle de tourniquet ou de Round Robin) suivant un ordre de priorité dynamique.
États d’un processus
Lorsqu’un programme est lancé, les instructions machine qui le composent sont chargées en mémoire de travail (RAM) : le processus associé est alors créé.
Pendant son existence au sein d’une machine, un processus peut avoir différents états :
- nouveau : le processus est en cours de création, l’exécutable est en mémoire et le PCB initialisé
- prêt (ready ou runnable) ou en attente (waiting) : le processus attend d’être affecté à un processeur
- élu (running) : les instructions du processus sont en cours d’exécution (il utilise le CPU)
- seul un processus peut être en exécution sur processeur à un instant donné.
- bloqué (blocked) ou endormi (sleeping) : le processus est interrompu en attente qu’un événement se produise
- terminé (terminated) : le processus est terminé (soit normalement, soit suite à une anomalie). il doit être déchargé de la mémoire par l’OS, et les ressources qu’il utilisait libérées.
- zombie : le processus est terminé mais ne peut pas être déchargé de la mémoire ...
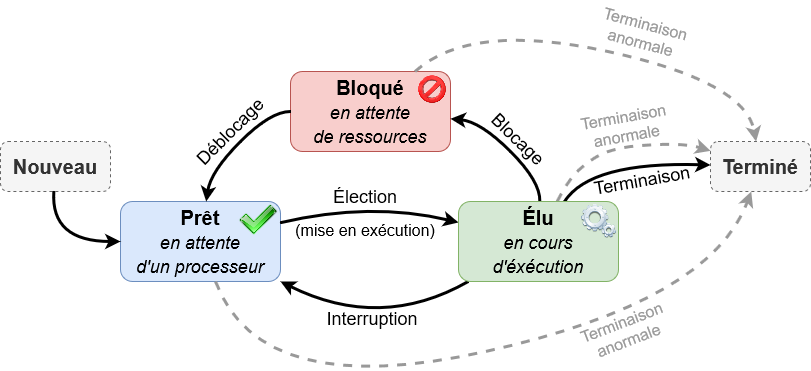
Ou plus simplement :
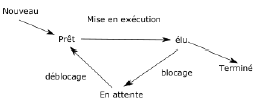
On peut utiliser la métaphore suivante : Cela ressemble à un professeur, qui a 3 paquets de copies à corigers !!!
3. Interblocage
Un processus peut être dans l'état bloqué dans l'attente de la libération d'une ressource.
Ces ressources (l'accès en écriture à un fichier, à un registre de la mémoire...) ne peuvent être données à deux processus à la fois. Des processus souhaitant accéder à cette ressource sont donc en concurrence sur cette ressource. Un processus peut donc devoir attendre qu'une ressource se libère avant de pouvoir y accéder (et ainsi passer de l'état Bloqué à l'état Prêt). Problème : Et si deux processus se bloquent mutuellement la ressource dont ils ont besoin ?
Exemple :
Considérons 2 processus A et B, et deux ressources R et S. L'action des processus A et B est décrite ci-dessous :

A l'étape A2 de A : problème, il faut pour cela pouvoir accèder à la ressource S, qui n'est pas disponible. L'ordonnanceur va donc passer A à Bloqué et va revenir au processus B qui redevient Élu. A l'étape B2 de B : problème, il faut pour cela pouvoir accèder à la ressource R, qui n'est pas disponible. L'ordonnanceur va donc passer B à Bloqué.
Les deux processus A et B sont donc dans l'état Bloqué, chacun en attente de la libération d'une ressource bloquée par l'autre : ils se bloquent mutuellement.
Cette situation (critique) est appelée interblocage ou deadlock.
Ce type de schéma fait apparaître un cycle d'interdépendance, qui caractérise ici la situation de deadlock.
Comment s'en prémunir ?
Il existe trois stratégies pour éviter les interblocages :
- la prévention : on oblige le processus à déclarer à l'avance la liste de toutes les ressources auxquelles il va accéder.
- l'évitement : on fait en sorte qu'à chaque étape il reste une possibilité d'attribution de ressources qui évite le deadlock.
- la détection/résolution : on laisse la situation arriver jusqu'au deadlock, puis un algorithme de résolution détermine quelle ressource libérer pour mettre fin à l'interblocage.
source : glassus

3.3 - Routage
Architectures matérielles, systèmes d’exploitation et réseaux
Protocoles de routage
Capacités Attendue :
Identifier, suivant le protocole de routage utilisé, la route empruntée par un paquet.
Commentaires :
- En mode débranché, les tables de routage étant données, on se réfère au nombre de sauts (protocole RIP) ou au coût des routes (protocole OSPF).
- Le lien avec les algorithmes de recherche de chemin sur un graphe est mis en évidence.
1. Résumé des épisodes précédents
cours de 1ère : Transmission de données dans un réseau, Protocoles de communication, Architecture d’un réseau (Réseaux 1 et 2)
Lorsqu'une machine A, d'adresse IP_A veut discuter avec une machine B, d'adresse IP_B :
-
La machine A calcule (grâce au masque de sous-réseau) si B est dans le même sous-réseau qu'elle, ou pas.
-
Si oui, elle peut donc connaître l'adresse MAC de la carte réseau de la machine B (soit elle la possède déjà dans sa table ARP, soit elle la demande en envoyant un message de broadcast à tout le sous-réseau : «qui possède cette adresse IP_B ?»). Elle envoie donc dans le sous-réseau une trame ayant pour entête l'adresse MAC de B : le switch lit cette trame, sait sur quel port est branché la machine B et lui envoie spécifiquement donc le message.
-
Si B n'est pas dans le même sous-réseau que A, A mettra en entête de sa trame l'adresse MAC de la carte réseau du routeur, qui joue le rôle de passerelle. Le routeur va ouvrir la trame et va observer l'IP_B, à qui il doit remettre ce message. C'est maintenant que vont intervenir les protocoles de routage :
- est-ce que B est dans le même sous-réseau que le routeur ?
- est-ce que B est dans un autre sous-réseau connu du routeur ?
- est-ce que B est totalement inconnu du routeur ?
Ces questions trouveront des réponses grâce à table de routage du routeur.
2. Tables de routage
Les tables de routage sont des informations stockées dans le routeur permettant d'aiguiller intelligemment les données qui lui sont transmises.
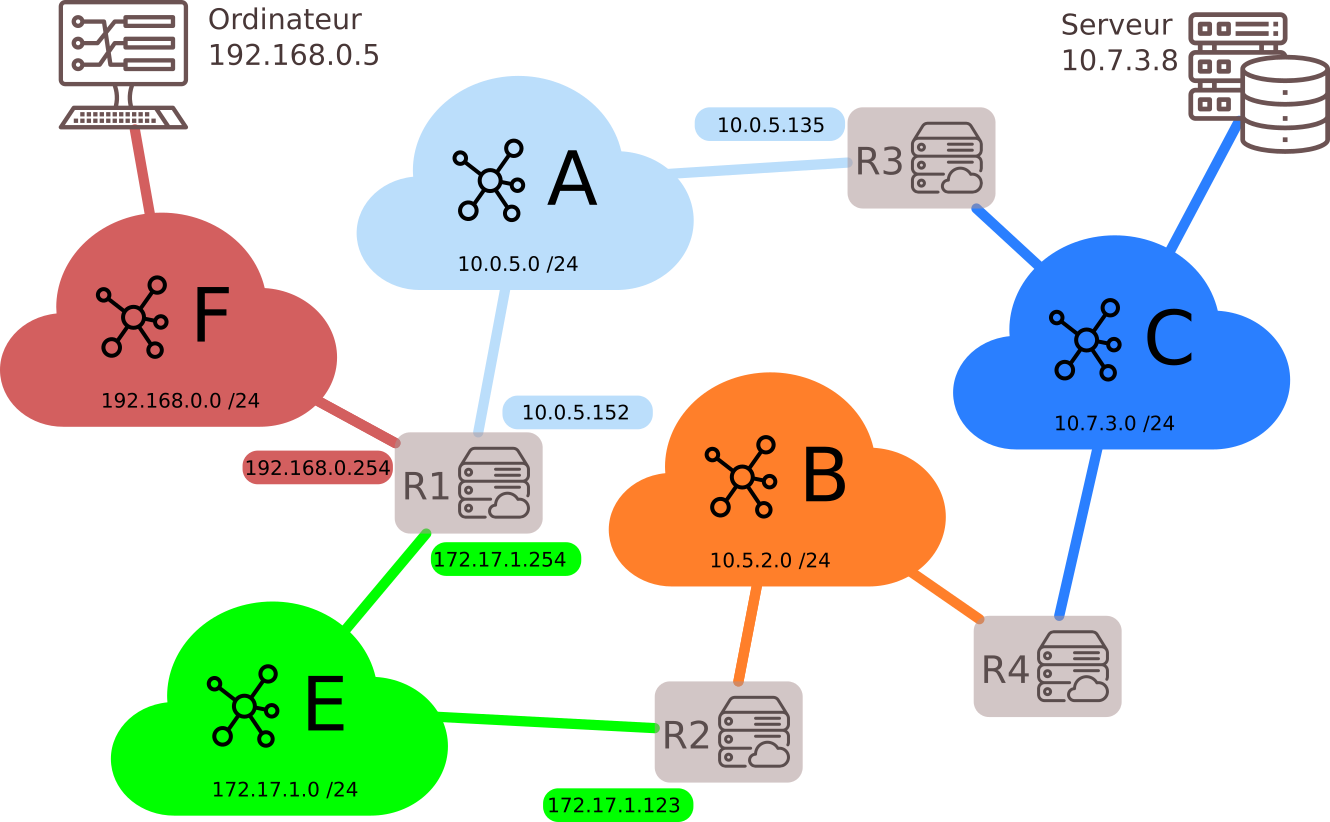
Dans le réseau ci-dessus, si l'ordinateur d'adresse 192.168.0.5 veut interroger le serveur 10.7.3.8 :
- l'adresse 10.7.3.8 n'étant pas dans le sous-réseau F (d'adresse 192.168.0.0 / 24), la requête est confiée au routeur via son adresse passerelle dans le réseau F (ici 192.168.0.254).
- le routeur observe si l'IP recherchée appartient à un autre des sous-réseaux auquel il est connecté. Ici, l'IP recherchée 10.7.3.8 n'appartient ni au sous-réseau A ou E.
- le routeur va donc regarder dans sa table de routage l'adresse passerelle d'un autre routeur vers qui elle doit rediriger les données. Si le sous-réseau C fait partie de sa table de routage, le routeur R1 saura alors que le meilleur chemin est (par exemple) de confier les données au routeur R3.
- si le sous-réseau C ne fait pas partie de la table de routage, le routeur R1 va alors le rediriger vers une route «par défaut» (que l'on peut assimiler au panneau «toutes directions» sur les panneaux de signalisation).
Interface et passerelle :
Les tables de routage des routeurs font très souvent apparaître deux colonnes, interface et passerelle, dont il ne faut pas confondre l'utilité :
-
interface: c'est l'adresse IP de la carte réseau du routeur par où va sortir le paquet à envoyer. Il y a donc toujours une adresse d'interface à renseigner. Parfois cette interface sera juste nommée interface1 ou interface2. -
passerelle: c'est l'adresse IP de la carte réseau du routeur à qui on va confier le paquet, si on n'est pas capable de le délivrer directement (donc si l'adresse IP de destination n'est pas dans notre propre sous-réseau). Cette adresse de passerelle n'est donc pas systématiquement mentionnée. Quand elle l'est, elle donne le renseignement sur le prochain routeur à qui le paquet est confié.
Exemple: table de routage du routeur R1

| Destination | Interface | Passerelle |
|---|---|---|
| F | 192.168.0.254 | |
| A | 10.0.5.152 | |
| E | 172.17.1.254 | |
| B | 172.17.1.254 | 172.17.1.123 |
| C | 10.0.5.152 | 10.0.5.135 |
Les trois réseaux F, A et E sont directement accessibles au routeur R1, puisqu'il en fait partie : il n'a donc pas besoin d'adresse passerelle pour communiquer avec ces réseaux.
Par contre, la communication avec le réseau B nécessite de confier le paquet au routeur R2 (c'est le choix de cette table de routage). Il faut donc mentionner l'adresse IP de ce routeur R2 (172.17.1.123), qu'on appelle adresse de passerelle.
De la même manière, la communication avec le réseau C nécessite de confier le paquet au routeur R3 (c'est le choix de cette table de routage). Il faut donc mentionner l'adresse IP de ce routeur R3 (10.0.5.135).
Comment sont construites les tables de routage ?
- Soit à la main par l'administrateur réseau, quand le réseau est petit : on parle alors de table statique.
- Soit de manière
dynamique: les réseaux s'envoient eux-mêmes des informations permettant de mettre à jour leurs tables de routages respectives. Des algorithmes de détermination de meilleur chemin sont alors utilisés : nous allons en découvrir deux, leprotocole RIPet leprotocole OSPF.
2. Le protocole RIP
Les règles du protocole RIP
Le Routing Information Protocol (RIP) est basé sur l'échange (toutes les 30 secondes) des tables de routage de chaque routeur.
Au début, chaque routeur ne connaît que les réseaux auquel il est directement connecté, associé à la distance 1.
Ensuite, chaque routeur va recevoir périodiquement (toutes les 30 secondes) la table des réseaux auquel il est connecté, et mettre à jour sa propre table suivant les règles ci-dessous :
- s'il découvre une route vers un nouveau réseau inconnu, il l'ajoute à sa table en augmentant de 1 la distance annoncée par le routeur qui lui a transmis sa table.
- s'il découvre une route vers un réseau connu mais plus courte (en rajoutant 1) que celle qu'il possède dans sa table, il actualise sa table.
- s'il découvre une route vers un réseau connu mais plus longue que celle qu'il possède dans sa table, il ignore cette route.
- s'il reçoit une route vers un réseau connu en provenance d'un routeur déjà existant dans sa table, s'il met à jour sa table car la topologie du réseau a été modifiée.
- si le réseau n'évolue pas (panne ou ajout de nouveau matériel), les tables de routage convergent vers une valeur stable. Elles n'évoluent plus.
- si un routeur ne reçoit pas pendant 3 minutes d'information de la part d'un routeur qui lui avait auparavant communiqué sa table de routage, ce routeur est considéré comme en panne, et toutes les routes passant par lui sont affectées de la distance infinie : 16.
Remarques et inconvénients:
- Le protocole RIP n'admet qu'une distance maximale égale à 15 (ceci explique que 16 soit considéré comme la distance infinie), ce qui le limite aux réseaux de petite taille.
- Chaque routeur n'a jamais connaissance de la topologie du réseau tout entier : il ne le connaît que par ce que les autres routeurs lui ont raconté. On dit que ce protocole de routage est du
routing by rumor. - La métrique utilisée (le nombre de sauts) ne tient pas compte de la qualité de la liaison, contrairement au protocole OSPF.
3. Le protocole OSPF
Un inconvénient majeur du protocole précédent est la non-prise en compte de la bande passante reliant les routeurs.
principe fondamental du protocole OSPF (Open Shortest Path First) : Le chemin le plus rapide n'est pas forcément le plus court.
En gris, le chemin RIP. En bleu, l'OSPF.Dans le protocole OSPF, les tables de routage vont prendre en considération la vitesse de communication entre les routeurs.
Dans une première phase d'initialisation, chaque routeur va acquérir (par succession de messages envoyés et reçus) la connaissance totale du réseau (différence fondamentale avec RIP) et de la qualité technique de la liaison entre chaque routeur.
Les différents types de liaison et leur coût
On peut, approximativement, classer les types de liaison suivant ce tableau de débits théoriques :
| Technologie | BP descendante | BP montante |
|---|---|---|
| Modem | 56 kbit/s | 48 kbit/s |
| Bluetooth | 3 Mbit/s | 3 Mbit/s |
| Ethernet | 10 Mbit/s | 10 Mbit/s |
| Wi-Fi | 10 Mbit/s ~ 10 Gbits/s | 10 Mbit/s ~ 10 Gbits/s |
| ADSL | 13 Mbit/s | 1 Mbit/s |
| 4G | 100 Mbit/s | 50 Mbit/s |
| Satellite | 50 Mbit/s | 1 Mbit/s |
| Fast Ethernet | 100 Mbit/s | 100 Mbit/s |
| FFTH (fibre) | 10 Gbit/s | 10 Gbit/s |
| 5G | 20 Gbit/s | 10 Gbit/s |
L'idée du protocole OSPF est de pondérer chaque trajet entre routeurs (comptant simplement pour «1» dans le protocole RIP) par une valeur de coût inversement proportionnelle au débit de transfert.
Par exemple, si le débit $d$ est exprimé en bits/s, on peut calculer le coût de chaque liaison par la formule : $coût = \frac{10^8}{d}$.
Cette formule de calcul peut être différente suivant les exercices, et sera systématiquement redonnée.
Néanmoins la valeur sera toujours au dénominateur, pour assurer la proportionnalité inverse du débit.
Avec cette convention, un route entre deux routeurs reliés en Fast Ethernet (100 Mbits/s) aura a un poids de 1, une liaison satellite de 20 Mbits/s aura un poids de 5, etc.
Reprenons le réseau suivant :

et simplifions-le en ne gardant que les liens entre routeurs, en indiquant leur débit :
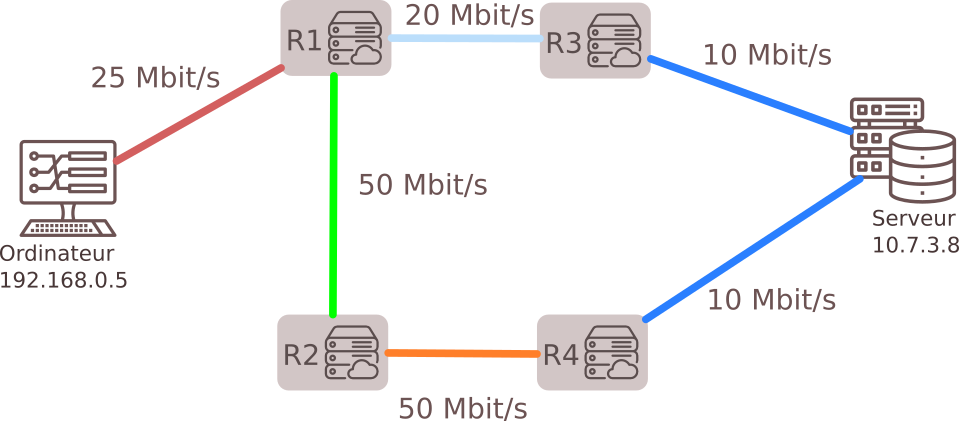
Notre réseau est devenu un graphe.
Nous allons pondérer ses arêtes avec la fonction coût introduite précédemment. L'unité étant le Mbit/s, l'arête entre R1 et R3 aura un poids de $coût = \frac{10^8}{20 000} = 5$.
Le graphe pondéré est donc :
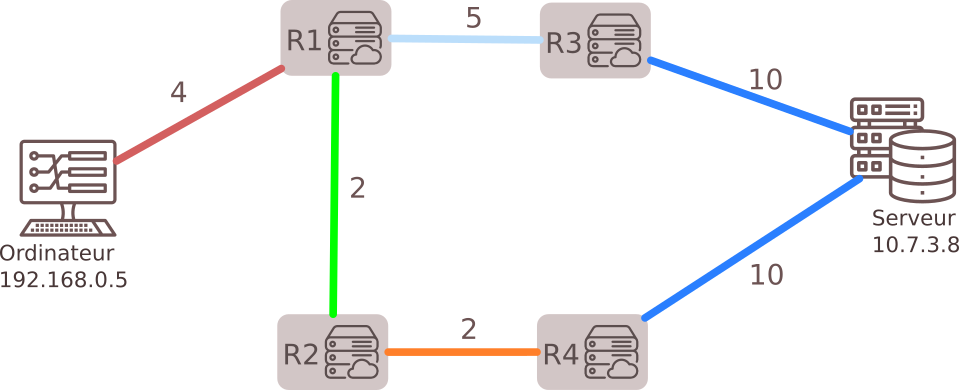
Le chemin le plus rapide pour aller de l'ordinateur au serveur est donc R1-R2-R4, et non plus R1-R3 comme l'aurait indiqué le protocole RIP.
Trouver le plus court chemin dans un graphe pondéré
L'exemple précédent était très simple et de solution intuitive. Dans le cas d'un graphe pondéré complexe, existe-t-il un algorithme de détermination du plus court chemin d'un point à un autre ? La réponse est oui, depuis la découverte en 1959 par Edsger Dijkstra de l'algorithme qui porte son nom, l'algorithme de Dijkstra.
Pour le comprendre, regarder la vidéo : Dijkstra
Exercice :
Donner le plus court chemin pour aller de E à F dans le graphe ci-dessous :
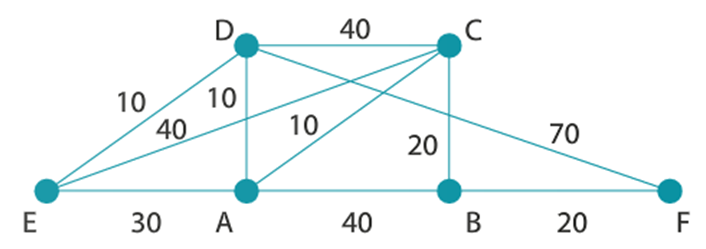
Réponse :
| E | A | B | C | D | F | Choix |
|---|---|---|---|---|---|---|
| 0 | -- | -- | -- | -- | -- | E(0) |
| . | 30vE | -- | 40vE | 10vE | -- | D(10) |
| . | 20vD | -- | 40vE | . | 80vD | A(20) |
| . | . | 60vA | 30vA | . | 80vD | C(30) |
| . | . | 50vC | . | . | 80vD | B(50) |
| . | . | . | . | . | 70vB | F(70) |
Le meilleur trajet est donc E-D-A-C-B-F. Attention ce trajet correspond à la colonne choix (dans l'ordre) mais c'est un hasard.
Exercice2 : (extrait du sujet 0)
On considère le réseau suivant :
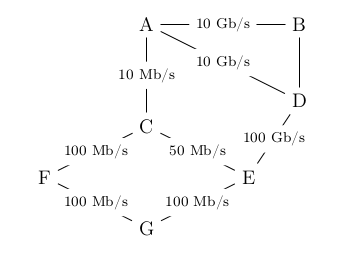
On rappelle que le coût d’une liaison est donné par la formule suivante : $coût = \frac{10^8}{d}$
-
Vérifier que le coût de la liaison entre les routeurs A et B est 0,01.
La liaison entre le routeur B et D a un coût de 5. Quel est le débit de cette liaison ?
-
Le routeur A doit transmettre un message au routeur G, en empruntant le chemin dont la somme des coûts sera la plus petite possible.
Déterminer le chemin parcouru. On indiquera le raisonnement utilisé.
Réponse :
-
$coût = \frac{10^8}{10x10^9} = 10^-2 = 0.01$
$5 = \frac{10^8}{d}$ donc $d =\frac{10^8}{5} = 2x10^7 = 20x10^6 = 20Mb/s$
-
On peut deviner le chemin de coût minimal entre A et G, qui est A-D-E-G (coût 1.011).
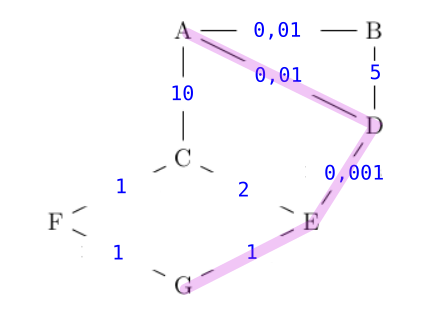
Pour le justifier, on peut (non obligatoire) faire un algorithme de Dijkstra :

Lien pour vérifier votre plus court chemin : Graph Online
source : glassus

3.4 - Congruences
Les congruences

Théorème de Bézout :
Si a et b sont des entiers non nuls, alors il existe des entiers relatifs x et y, et un entier d tels que ax + by = d où d est le PGCD de a et b.
Démonstration :
Considérons l'ensemble S de toutes les combinaisons ax + by, où x et y sont des entiers relatifs.
S contient au moins un élément positif non nul, par exemple l'entier a.
Donc l'ensemble S, il existe un plus petit élément positif, que nous appellerons d.
Par définition de S, il existe des entiers x0 et y0 tels que d = ax0 + by0.
Pour montrer que d divise à la fois a et b, considérons la division euclidienne de a par d>0 :
a = dq + r, où 0 ≤ r < d.
Donc r = a - dq = a - (ax0 + by0)q = a(1-qx0) + b(-qy0).
Donc r appartient à S et 0 ≤ r < d.
Par construction, d est le plus petit élément positif non nul de S, donc r = 0.
Ainsi, d divise a.
Un raisonnement similaire montre que d divise b.
Donc d est un diviseur commun de a et b.
Si un autre nombre d' est aussi un diviseur commun de a et b, alors comme d = ax0 + by0, cette autre nombre d' divisera d.
Par conséquent, d est le PGCD de a et b.
Algorithme d'Euclide (Classe de 3ième) ou PGCD de a et b
PDCD(a,b) = ?
1er cas : si b = 0
PDCD(a,b) = PDCD(a,0) = a
2ième Cas : si b > 0
Posons a = qb + r où q est le quotient et r est le reste de la division euclidienne de a par b.
d = PGCD(a,b) = PGCD(b,r)
def pgcd(a, b):
if b == 0:
return a
else:
return pgcd(b, a % b)
# Exemple d'utilisation
a = 91
b = 77
print("Le PGCD de", a, "et", b, "est :", pgcd(a, b))Le PGCD de 91 et 77 est : 7
Algorithme d'Euclide étendu ou comment trouver des coefficients x et y de Bezout et le PDCD de a et b
1er cas : si b = 0
d =a, x = 1, y = 0 est une solution de ax + by = d
2ième Cas : si b > 0
ax + by = d <=> (qb + r)x + by = d <=> b(qx + y) + rx = d <=> bx1 + ry1 = d avec x1 = qx + y et y1 = x <=> bx1 + ry1 = d avec x = y1 et y = x1 - qy1
def euclide_etendu(a, b):
if b == 0:
return a, 1, 0
else:
pgcd, x1, y1 = euclide_etendu(b, a % b)
x = y1
y = x1 - (a // b) * y1
return pgcd, x, y
# Exemple d'utilisation
a = 91
b = 77
pgcd, x, y = euclide_etendu(a, b)
print(f"Une solution de {a}x + {b}y = d est {a}({x}) + {b}({y}) = {pgcd}.")Une solution de 91x + 77y = d est 91(-5) + 77(6) = 7.
Théorème de Gauss :
Si a, b et c sont des entiers non nuls.
Si a divise le produit bc et si a et b sont premiers entre eux alors a divise c.
Démonstration :
a divise bc, donc il existe k entier tel que bc = ka.
a et b sont premiers entre eux donc il existe deux entiers u et v tels que au + bv = 1.
D'où c = cau + cbv et bc = ka, donc c = cau + kav = a(cu + kv) ce qui prouve que a divise c.
Définition de la Congruence :
Soient a, b, n des entiers relatifs.
On dit que a est congruent à b modulo n, noté a≡b (mod n) ou a≡b[n], si n divise la différence a−b.
Propriétés des Propriétés de Congruence :
- Réflexivité : Pour tout entier relatif a, a ≡ a [n].
- Symétrie : Si a et b sont des entiers relatifs et a ≡ b [n], alors b ≡ a [n].
- Transitivité : Si a, b, et c sont des entiers relatifs et a ≡ b [n] et b ≡ c [n], alors a ≡ c [n].
- Addition : Si a, b, c, et d sont des entiers relatifs et a ≡ b [n] et c ≡ d [n], alors a + c ≡ b + d [n].
- Soustraction : Si a, b, c, et d sont des entiers relatifs et a ≡ b [n] et c ≡ d [n], alors a - c ≡ b - d [n].
- Multiplication : Si a, b, c, et d sont des entiers relatifs et a ≡ b [n] et c ≡ d [n], alors a * c ≡ b * d [n].
- Puissance : Si a et b sont des entiers relatifs et a ≡ b [n], alors ak ≡ bk [n] pour tout entier k.
- Petit Théorème de Fermat : Si p est un nombre premier et a est un entier relatif non divisible par p, alors ap-1 ≡ 1 [p].
Démonstrations des Propriétés de Congruence
- Réflexivité
- Symétrie
- Transitivité
- Addition
- Soustraction
- Multiplication
- Puissance
- Petit Théorème de Fermat
La différence a - a est égale à 0.
Comme n divise tout nombre entier multiple de 0 (car n × 0 = 0), n divise a - a.
Donc, a ≡ a [n].
a ≡ b [n]
Donc il existe un entier relatif k tel que a - b = nk.
Donc b - a = -nk.
Donc, b ≡ a [n].
a ≡ b [n].
Donc il existe un entier relatif k tel que a - b = nk.
b ≡ c [n].
Donc il existe un entier relatif l tel que b - c = nl.
En additionnant ces deux équations, on obtient (a - b) + (b - c) = nk + nl.
Donc a - c = n(k + l).
Donc a ≡ c [n].
a ≡ b [n]
Donc il existe un entier relatif k tel que a - b = nk.
c ≡ d [n]
Donc il existe un entier relatif l tel que c - d = nl.
En additionnant ces deux équations, on obtient (a + c) - (b + d) = n(k + l).
Donc a + c ≡ b + d [n].
a ≡ b [n]
Donc il existe un entier relatif k tel que a - b = nk.
c ≡ d [n]
Donc il existe un entier relatif l tel que c - d = nl.
Par soustraction de ces deux équations, on obtient a - b - c + d = nk - nl.
Donc (a - c) - (b - d) = n(k - l).
Donc a - c ≡ b - d [n].
a ≡ b [n].
Donc il existe un entier k tel que a = b + nk.
c ≡ d [n].
Donc il existe un entier l tel que c = d + nl.
En multipliant ces deux équations, on obtient ac = (b + nk)(d + nl).
Donc ac = bd + bnl + nkd + nknl.
Donc ac = bd + n (bl + kd + knl).
Donc ac ≡ bd [n].
Soit P(k) la propriété ak ≡ bk [n] pour tout entier k.
Initialisation :
Pour k = 1, a1 ≡ b1 [n] se réduit à a ≡ b [n], ce qui est notre hypothèse de départ.
Donc, la propriété est vraie pour k = 1.
Hérédité :
Supposons que la propriété soit vraie pour un certain entier k, c'est-à-dire ak ≡ bk [n]
a ≡ b [n] et ak ≡ bk [n]
D'après la propriété de Multiplication, on a : ak * a ≡ bk * b [n].
Donc ak+1 ≡ bk+1 [n].
Par récurrence, la propriété est donc vraie pour tout entier 1 ≤ k .
Démontrons cette propriété par récurrence.
Soit P(a): ap ≡ a [p] pour tout entier a.Initialisation :
Pour a = 0
0p = 0, donc 0p ≡ 0[p].
Donc P(0) est vraie.
Hérédité :
Supposons que la propriété soit vraie pour un certain entier a, c'est-à-dire ap ≡ a [p].
Formule du binôme :
(a+1)p = 1 + $\binom{p}{1}$a + ... + $\binom{p}{p-1}$ap-1 + ap
coefficient binomial :
Pour tous les entiers k et p, avec 0 ≤ k ≤ p
\( \binom{p}{k} = \frac{p!}{k!(p-k)!} \) et ce nombre est un nombre entier.
Donc pour tout entier k tel que 1 ≤ k ≤ p-1, on a : \( k \cdot \binom{p}{k} = k \times \frac{p!}{k!(p-k)!} = \frac{p \times (p-1)!}{(k-1)!(p-k)!} = p \times \binom{p-1}{k-1} \)
Donc pour tout entier k tel que 1 ≤ k ≤ p-1, on a : p divise \( k \cdot \binom{p}{k} \).
1 ≤ k ≤ p-1 donc p ne divise pas k.
p divise \( k \cdot \binom{p}{k} \)
Donc d'après le théorème de Gauss, on a : p divise \( \binom{p}{k} \).
Donc tout entier k tel que 1 ≤ k ≤ p-1, on a : \( \binom{p}{k} \) ≡ 0[p]
Donc (a+1)p ≡ 1+ap[p].
Et par l'hypothèse de récurrence, on a : ap ≡ a [p].
Donc (a+1)p ≡ 1+a[p].
Donc (a+1)p ≡ a+1 [p].
Par récurrence, la propriété ap ≡ a [p] est donc vraie pour tout entier 0 ≤ a .
Donc ap ≡ a [p] est donc vraie pour tout entier 1 ≤ a.
Donc ap - a ≡ 0 [p] est donc vraie pour tout entier 1 ≤ a.
Donc a(ap-1 - 1) ≡ 0 [p] est donc vraie pour tout entier 1 ≤ a.
a est un entier relatif non divisible par p.
Donc d'après le théorème de Gauss, on a : p divise ap-1 - 1.
Donc ap-1 - 1 ≡ 0 [p] pour tout entier 1 ≤ a où a est un entier relatif non divisible par p.
Critère de Divisibilité par 9
Un nombre entier est divisible par 9 si et seulement si la somme de ses chiffres est divisible par 9.
Démonstration :
Soit un nombre entier N.
N = 10nanan + 10n-1an-1+...+102a2+ 10a1 où ak sont ses chiffres.
10 ≡ 1 [9]
Donc pour tout entier k, on a : 10k ≡ 1 [9]
Donc N ≡ an + an-1 + ... + a0 [9]
3.5 - RSA
Architectures matérielles, systèmes d’exploitation et réseaux
Sécurisation des communications.
Capacités Attendue :
- Décrire les principes de chiffrement symétrique (clef partagée) et asymétrique (avec clef privée/clef publique).
- Décrire l’échange d’une clef symétrique en utilisant un protocole asymétrique pour sécuriser une communication HTTPS.
Commentaires :
- Les protocoles symétriques et asymétriques peuvent être illustrés en mode débranché,éventuellement avec description d’un chiffrement particulier.
- La négociation de la méthode chiffrement du protocole SSL (Secure Sockets Layer) n’est pas abordée.
1. Un exemple de Chiffrement symétrique :
Propriété :
Pour tous les nombre entiers a et b, on a :
(a XOR b) XOR b = a.
Démonstration :
(0 XOR 0) XOR 0 = 0 XOR 0 = 0
(0 XOR 1) XOR 1 = 1 XOR 1 = 0
(1 XOR 0) XOR 0 = 1 XOR 0 = 1
(1 XOR 1) XOR 1 = 0 XOR 1 = 1
Et donc dans chaque scénario, (a XOR b) XOR b = a.
Le XOR est noté ^ en python.
masque = "CETTEPHRASEESTVRAIMENTTRESTRESLONGUEMAISCESTFAITEXPRES"
def chiffre(message, masque):
message_chiffre = ""
for i in range(len(message)):
lettre_chiffree = chr(ord(message[i]) ^ ord(masque[i]))
message_chiffre += lettre_chiffree
return message_chiffre
message ="Je suis le plus FORT !"
message_crypté = chiffre(message, masque)
print("message crypté :", message_crypté)
mesage_décrypté = chiffre(message_crypté, masque)
print("message décrypté :",mesage_décrypté)Dans un chiffrement symétrique, c'est la même clé qui sert au chiffrement et au déchiffrement.
Avantage d'un chiffrement symétrique :
Les chiffrements symétriques sont souvent rapides, consommant peu de ressources, et donc adaptés au chiffrement de flux important d'informations. Par exemple, la sécurisation des données transitant par le protocole https est basée sur un chiffrement symétrique.
Inconvénient d'un chiffrement symétrique :
La clé ! Si deux personne ont besoin d'utiliser un chiffrement pour se parler, comment peuvent-ils échanger leurs clés puisque leur canal de transmission n'est pas sûr ! Le chiffrement symétrique impose qu'Alice et Bob aient pu se rencontrer physiquement au préalable pour convenir d'une clé secrète, ou bien qu'ils aient réussi à établir une connexion sécurisée pour s'échanger cette clé.
Principe de Kerckhoffs :
La sécurité d'un système de chiffrement ne doit reposer que sur le secret de la clé, et non pas sur la connaissance de l'algorithme de chiffrement. Cet algorithme peut même être public (ce qui est pratiquement toujours le cas).
2. Chiffrement asymétrique
Inventé par Whitfield Diffie et Martin Hellman en 1976, le chiffrement asymétrique vient résoudre l'inconvénient essentiel du chiffrement symétrique : le nécessaire partage d'un secret (la clé) avant l'établissement de la communication sécurisée.
2.1 Principe du chiffrement asymétrique
Le principe de base est l'existence d'une clé publique, appelée à être distribuée largement, et d'une clé privée, qui ne quitte jamais son propriétaire.

2.2 Communication authentifiée.
Dans la situation du 2.1, Alice, qui a distribué largement sa clé publique, ne peut pas s'assurer que le message vient bien de Bob.
Avec le protocole ci-dessous permet de s'assurer que chaque personne est bien celle qu'elle prétend être : on résout le problème d'authentification.
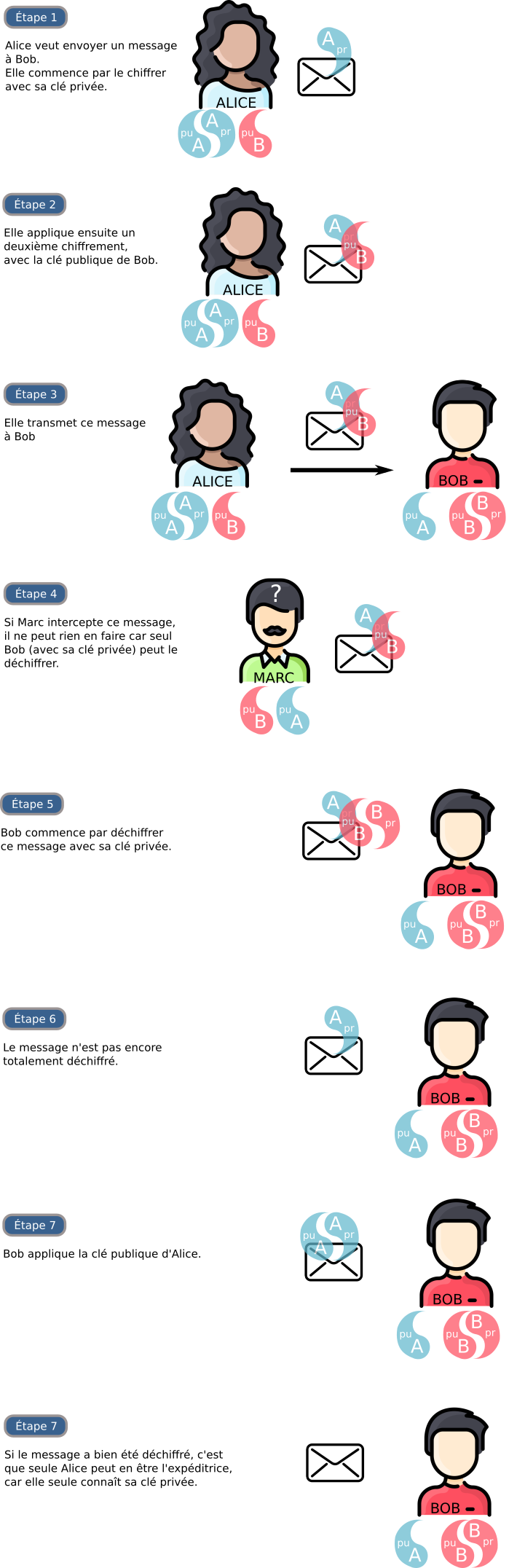
2.3 Méthode du chiffrement RSA :
En 1977, trois chercheurs du MIT, Ron Rivest, Adi Shamir et Len Adleman créent le premier protocole concret de chiffrement asymétrique : le chiffrement RSA.

Clifford Cocks est le véritable inventeur du RSA... mais le reste du monde ne l'apprendra qu'en 1997 au moment de la déclassification de cette information. Il avait fait cette découverte 3 ans auparavant.

Étape 1
On choisit 2 grands nombres premiers p = 11 et q = 17.
Dans la réalité ces nombres seront vraiment très grands, plus de 100 chiffres.
Étape 2
on pose n = pq.
donc n = 11 x 17 = 187
Avec de très grans nombre, il est extrêmement difficile de trouver q et p en partant de n, cela prend un temps exponentiel.
La robustesse du système RSA repose sur cette difficulté de factorisation.
Étape 3
On choisit un nombre e qui doit être premier avec phi = (p-1)(q-1) et qui est différent de 1.
Ici phi = (p-1)(q-1) = (11-1)(17-1) = 10x16 = 160
160= 2x5x2x2x2
donc nous pouvons choisir e = 3.
Mais nous aurions pu choisir 3,7,9,11,13,17,19,21,23...
Le couple (e,n) est la clé publique, elle peut être diffusé à qui veut nous écrire.
donc (e,n) = (3,187).
Étape 4
On calcule maintenant la clé privée, on doit trouver un nombre d qui vérifie l'égalité ed $\equiv 1 [phi]$.
donc 3d $\equiv 1 [160]$
3 x 107 = 321 = 2 x 160 + 1
donc on peux choisir d = 107
En pratique, il existe l'Algorithme d'Euclide étendu pour trouver cette valeur d, appelée inverse de e.
Le couple (d,n) est la clé privée. Elle ne doit pas être diffusée.
donc (d,n) = (107,187).
Étape 5
Supposons que Bob veuille écrire à Alice pour lui envoyer la lettre 'J', soit le nombre ord('J')=74.
Il possède la clé publique d'Alice, qui est (e,n) = (3,187)
Il calcul $74^3$ = 405 224 = 2 166 x 187 + 182 donc $74^3 \equiv 182[187]$
C'est cette valeur 182 qu'il transmet à Alice.
Si Marc intercepte cette valeur 182, même en connaissant la clé publique d'Alice (3,187), il peut résoudre l'équation $x^3 \equiv 182[187]$ (voir programme ci-dessous) mais pas de manière efficace lorsque il y a de grands nombres.
Étape 6
Alice reçoit la valeur 182.
La clé privée de Alice est (d,n) = (107,187)
Il lui "suffit !!!" alors d'élever 182 à la puissance 107 (sa clé privée), et de calculer le reste modulo 187 :
$182^{107}$
= 67241673631537193934036117101479548806501991262111002001744254706233567920890614697211406837000572401237441319454792304933033591086665839294597750916081076542143576548003513761297726915976490281874033126212146214405576504503866998629825773568
= 187 x 18060028181057512288308845553797179459401200529078752358110793195031781145697580921395102159974556894430381933341233949598704423208702796527307650511078722855725227084557548715716316244005752915438897000961 + 74
$\equiv 74[187]$
La valeur 74, qui est bien le message original de Bob.
Pourquoi ça marche ?
Grâce au Théorème de Bezout :
comme e et phi sont premiers entre eux, il existe des entiers u et v tel que u.e + v.phi = 1
donc $u.e \equiv 1 [phi]$
donc il existe d tel que $d.e \equiv 1 [phi]$
donc il existe d tel que $d.e \equiv 1 [(p-1)(q-1)]$
Grâce au Petit Théorème de Fermat :
Si p est un nombre premier et a n'est pas divisible par p, alors $a^{p-1} \equiv 1 [p]$.
Soit m un nombre qui n'est pas divisible par p et qui n'est pas divisible par q.
donc d'après le Petit Théorème de Fermat : $m^{p-1} \equiv 1 [p]$ et $m^{q-1} \equiv 1 [q]$
donc $m^{(p-1)(q-1)} = (m^{p-1})^{q-1} \equiv 1^{q-1} [p] \equiv 1 [p]$
de même $m^{(p-1)(q-1)} = (m^{q-1})^{p-1} \equiv 1^{p-1} [q] \equiv 1 [q]$
p et q sont des nombres premiers donc d'après le Théorème de Gauss, on a : $m^{(p-1)(q-1)} \equiv 1 [pq]$
n = pq
donc $m^{(p-1)(q-1)} \equiv 1 [n]$
On a posait d tel que ed $\equiv 1 [(p-1)(q-1)]$
donc il existe un nombre entier k tel que ed = (p-1)(q-1)k + 1
donc $m^{ed} = m^{(p-1)(q-1)k + 1} = m(m^{(p-1)(q-1)}) = m[n] $
Et donc dans notre exemple :
$74^3 \equiv 182[187]$ donc $(74^3)^d \equiv 182^d[187]$ donc $182 ^ d \equiv (74^3)^d [187]$
donc $182^{107} = 182 ^ d \equiv (74^3)^d [187] \equiv (74^e)^d [n] \equiv 74^{ed}[n] \equiv 74[n] \equiv 74[187]$
Remarques :
- Les rôles de la clé publique et de la clé privée sont symétriques : un message chiffré avec la clé publique se déchiffrera en le chiffrant avec la clé privée, tout comme un message chiffré avec la clé privée se déchiffrera en le chiffrant avec la clé publique.
- le calculs du $base^{exponent} \equiv modulus$ peut-être très compliqué, on doit souvent utiliser la méthode de exponentiation modulaire (voir programme python ci-dessous)
RSA, un système inviolable ?
Le chiffrement RSA a des défauts (notamment une grande consommation des ressources, due à la manipulation de très grands nombres). Mais le choix d'une clé publique de grande taille (actuellement 1024 ou 2048 bits) le rend pour l'instant inviolable.
Deux évènements pourraient faire s'écrouler la sécurité du RSA :
- la découverte d'un algorithme efficace de factorisation, capable de tourner sur les ordinateurs actuels. Cette annonce est régulièrement faite, et tout aussi régulièrement contredite par la communauté scientifique.
- l'avènement d'ordinateurs quantiques, dont la vitesse d'exécution permettrait une factorisation rapide. Il est à noter que l'algorithme de factorisation destiné à tourner sur un ordinateur quantique existe déjà : l'algorithme de Schor.
def gcd(a, b):
while b:
a, b = b, a % b
return a
def find_e(phi):
e = 2
while e < phi:
if gcd(e, phi) == 1:
return e
e += 1
raise Exception('Aucun e approprié trouvé')
p = 11
q = 17
phi = (p-1) * (q-1)
e = find_e(phi)
print(f"e = {e}")# Algorithme d'Euclide étendu
def extended_gcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = extended_gcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(e, phi):
g, x, y = extended_gcd(e, phi)
if g != 1:
raise Exception("L'inverse modulaire n'existe pas")
else:
return x % phi
n = p * q
# Calcul de phi et d
phi = (p-1) * (q-1)
d = modinv(e, phi)
print(f"p = {p}, q = {q}")
print(f"n = {n}")
print(f"e = {e}")
print(f"phi = {phi}")
print(f"d = {d}")Exponentiation Modulaire
L'idée de base de l'exponentiation modulaire est de décomposer l'exponentiation en une série de carrés et de multiplications, en utilisant le fait que :
$ab [m] = (a [m]) (b [m]) [m]$
Donc, au lieu de calculer $182^{107}$ directement, ce qui serait très coûteux en termes de calculs, nous décomposons l'exposant en puissances de 2, et calculons modulo 187 à chaque étape pour garder les nombres gérables.
Commençons par représenter l'exposant 107 en binaire :
$107 = 2^6 + 2^5 + 2^3 + 2^1 + 2^0$
$107 = 1101011$ en binaire
En utilisant cette représentation, $182^{107}$ est décomposé comme : $182^{107}$ = $182^{(2^6)}$ x $182^{(2^5)}$ x $182^{(2^3)}$ x $182^{(2^1)}$ x $182^{(2^0)}$
Nous allons maintenant calculer la valeur de $182^{107} [187]$ en utilisant cette décomposition et la propriété mentionnée précédemment.
$182^{(2^0)} = 182 [187]$
$182^{(2^1)} = 33 124 = 25[187]$
$182_25 = 4 550 = 62[187]$
$182^{(2^2)} = (182^{(2^1)})^2 = 25^2[187] = 625[187] = 64[187]$
$182^{(2^3)} = (182^{(2^2)})^2 = 64^2[187] = 4096[187] = 169[187]$
$62_169 = 10 478[187] = 6[187]$
$182^{2^4} = (182^{(2^3)})^2= 169^2[187] = 28 561[187] = 137[187]$
$182^{2^5} = (182^{(2^4)})^2= 137^2[187] = 18 769[187] = 69[187]$
$69_6 = 414 = 40[187]$
$182^{2^6} = (182^{(2^5)})^2 = 69^2[187] = 4761[187] = 86[187]$
$86_40 = 3440 = 74[187]$
# Exponentiation modulaire
def mod_pow(base, exponent, mod):
binary_exponent = bin(exponent)[2:]
result = 1
base = base % mod
for bit in reversed(binary_exponent):
if bit == '1':
result = (result * base) % mod
base = (base * base) % mod
return result
base = 182
exponent = 107
modulus = 187
result = mod_pow(base, exponent, modulus)
print(f"Résultat final : {base}^{exponent} mod {modulus} = {result}")# RSA
def rsa_encrypt(message, e, n):
encrypted = [mod_pow(ord(char), e, n) for char in message]
return encrypted
def rsa_decrypt(encrypted, d, n):
decrypted = ''.join([chr(mod_pow(num, d, n)) for num in encrypted])
return decrypted
print(f"p = {p}, q = {q}")
print(f"n = p x q = {n}")
print(f"e = {e}")
print(f"d = {d}")
message = "Je suis le plus FORT!"
print(f"message : {message}")
encrypted_message = rsa_encrypt(message, e, n)
print(f"Message chiffré: {encrypted_message}")
decrypted_message = rsa_decrypt(encrypted_message, d, n)
print(f"Message déchiffré: {decrypted_message}")# Résolution de 𝑥^3≡182[187] avec l'exponentiation modulaire
for k in range(201):
if mod_pow(k, 3, 187) == 182:
print(k)3. HTTPS : exemple d'utilisation conjointe d'un chiffrement asymétrique et d'un chiffrement symétrique.
Plus de 90 % du trafic internet est chiffré avec HTTPS, combinant :
TLS : Génère une clé partagée via chiffrement asymétrique.
HTTP : Transmet les données chiffrées avec la clé partagée (AES).Le chiffrement asymétrique, trop lent, est utilisé uniquement pour l'échange de clés, tandis que le chiffrement symétrique, plus rapide, gère le reste.
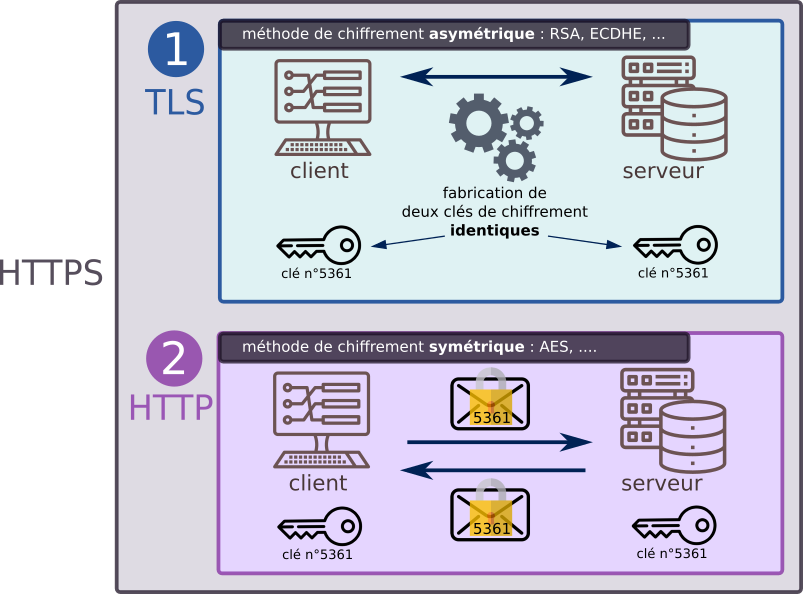
4.1 - Programme en tant que donnée
Langages et programmation
Notion de programme en tant que donnée. Calculabilité, décidabilité.
Capacités Attendue :
- Comprendre que tout programme est aussi une donnée.
- Comprendre que la calculabilité ne dépend pas du langage de programmation utilisé.
- Montrer, sans formalisme théorique, que le problème de l’arrêt est indécidable.
Commentaires :
L’utilisation d’un interpréteur ou d’un compilateur, le téléchargement de logiciel, le fonctionnement des systèmes d’exploitation permettent de comprendre un programme comme donnée d’un autre programme.
1. Notion de programme en tant que donnée
Nous allons tout d'abord expliciter un point important qui sera le fondement de la théorie de la calculabilité : un programme est aussi une donnée.
Cela peut paraître étonnant à première vue puisqu'on est habitué à traiter :
- les programmes dans des fonctions,
- les données dans des variables.
Fonctions et variables sont des objets de nature différente en apparence. Si on se raccroche à ce que l'on connaît en python, une fonction se déclare avec le mot clé def et une variable s'initialise avec l'opérateur d'affectation =.
Prenons en exemple l'algorithme d'Euclide, un algorithme vieux de plus de 2500 ans, permettant de calculer le PGCD de 2 nombres. On peut l'écrire à l'aide d'une fonction Python:
def euclide(a,b):
if a < b:
a,b=b,a
while b:
a,b=b,a%b
return a
euclide(35, 49)Dans ce programme Python, euclide est une fonction et a et b sont des données. Ils ne semblent pas être de nature comparable.
Et pourtant, à y regarder de plus près, notre algorithme programmé dans la fonction euclide n'est rien d'autre qu'une succession de caractères. On peut même pousser la réflexion jusqu'à créer une chaîne de caractère contenant ce programme :
mon_programme = "def euclide(a,b):\n\tif a < b: a,b=b,a\n\twhile b: a,b=b,a%b\n\treturn a"Maintenant mon algorithme est devenu une variable. On peut alors construire une machine universelle capable d'évaluer n'importe quelle donnée contenant un algorithme formalisé dans le langage Python :
def universel(algo, *args):
exec(algo)
ligne1 = algo.split('\n')[0]
nom = ligne1.split('(')[0][4:]
return eval(f"{nom}{args}")A présent, il est possible d'invoquer la machine universelle en lui passant en données :
- la variable contenant mon algorithme;
- les arguments sur lequel celui-ci va travailler et obtenir la réponse.
universel(mon_programme, 35, 49)Dans l'exemple ci-dessus, vous pouvez constater que le programme et les données sur lesquelles il agit sont de même nature : ce sont 3 variables passées en paramètres à ma fonction universelle. on en déduit donc :
Certains programmes utilisent comme données le code source d'autres programmes. Les compilateurs sont des bons exemples.Une fois le code source terminée, le compilateur (qui est un logiciel comme un autre) "transforme" ce code source en langage machine.
Il existe d'autres exemples de programmes qui utilisent comme données d'autres programmes :
- un système d'exploitation peut être vu comme un programme qui fait "tourner" d'autres programmes
- pour télécharger un logiciel on utilise un gestionnaire de téléchargement qui est lui-même un logiciel.
On trouve même des programmes capables de détecter certaines erreurs dans le code source d'autres programmes ou même encore des programmes capables de prouver (mathématiquement parlant) qu'un autre programme est correct (qu'il fait bien ce pour quoi il a été conçu).
2. Décidable, calculable
Un problème de décision est dit décidable s'il existe un algorithme, une procédure mécanique qui se termine en un nombre fini d'étapes, qui le décide, c'est-à-dire qui réponde par oui ou par non à la question posée par le problème.
S'il n'existe pas de tels algorithmes, le problème est dit indécidable.
Exemples :
- Un problème décidable :
Soit x un nombre entier , le problème " est-il pair ?" est décidable, car il existe un algorithme qui se termine en un temps fini qui décide si oui ou non x est pair.
- Un problème indécidable : Paradoxe du barbier
Dans une ville, il y a un barbier (et un seul) qui suit la règle suivante :- Le barbier rase tous les hommes qui ne se rasent pas eux-mêmes.
- Et seulement ceux-là. La question est alors : "Qui rase le barbier ?"
Une fonction ƒ est une fonction calculable s'il existe une méthode précise qui, étant donné un argument , permet d'obtenir l'image en un nombre fini d'étapes.
Exemples :
- Une fonction calculable :
Soit x un entier, la fonction "Quel est le reste de la division euclidienne de x par 2 ?" est calculable. Il existe un algorithme qui se termine en un temps fini qui calcule le reste de la division euclidienne de x par 2.
- Une fonction non calculable : "Qui rase le barbier ?" du paradoxe du barbier.
Attention :
Si un problème est indécidable cela ne veut pas dire que l’on n’est pas capable de résoudre ce problème, cela veut juste dire qu’il n’existe pas d’algorithme capable de résoudre ce problème.
Par exemple :
Soient f et g deux fonctions, et deux programmes def fonction_f(x): return f(x) et def fonction_g(x): return g(x).
Les programmes sont-ils égaux ?
On ne peut pas tester une infinité de valeurs.
3. Le problème de l’arrêt est indécidable.
Vidéo : Fabrizio Bucella Université de Bruxelles - Physicien

 L'existence des problèmes indécidables a été prouvé en 1937 par Alonzo Church et Alan Turing.
L'existence des problèmes indécidables a été prouvé en 1937 par Alonzo Church et Alan Turing.
Voici une version de la démonstration du problème de l'arrêt, telle qu'introduite par Alan Turing, sans formalisme !
Démonstration :
Raisonnon par l'absurde
Supposons l'existence d'un programme nommé $H$, capable de décider du problème de l'arrêt.
Ce programme $H$ prend en entrée un programme $P$ et une entrée $X$.
Création d'un programme contradictoire
Construisons maintenant un programme $D_H$ utilisant $H$.
$D_H$ prend en entrée un programme $P$ et fait ce qui suit :
Contradiction
- 1er cas : Si $H(D_H,D_H) = oui$
Donc $D_H$ s'arrête avec $D_H$ comme entrée.
Mais, par définition de $D_H$, $D_H$ doit entrer dans une boucle infinie, ce qui est une contradiction.
- 2ième cas : Si $H(D_H,D_H) = non$
Donc $D_H$ entre dans une boucle infinie avec $D_H$ comme entrée.
Mais, par définition de $D_H$, $D_H$ doit s'arrêter, ce qui est une contradiction.
Conclusion :
Il n'existe pas d'algorithme général qui puisse déterminer si un autre algorithme s'arrête ou non pour toutes les entrées possibles.

4.2 - Récursivité ✔
Terminale NSI - Programmation : récursion
Capacités attendues :
- Écrire un programme récursif.
- Analyser le fonctionnement d’un programme récursif.
Commentaire :
Des exemples relevant de domaines variés sont à privilégier.
1) Méthode itérative
Une fonction itérative est une fonction dans laquelle des instructions sont exécutées dans des boucles while ou for.
On souhaite implémenter une fonction somme() prenant nen argument, et qui renvoie la somme des n premiers entiers.
Par exemple :
>>> somme(5)
15on calcule la somme 0 + 1 + 2 + 3 + 4 + 5, ce qui fait 15.
def somme_iteratif(n):
total = 0
for nombre in range(0, n+1, 1):
total = total + nombre
return total
somme_iteratif(5)from tutor import tutor
def somme_iteratif(n):
total = 0
for nombre in range(0, n+1, 1):
total = total + nombre
return total
somme_iteratif(5)
tutor()a) Combien de fois la fonction somme_iteratif est-elle exécutée ?
Réponse : La fonction somme_iteratif est exécutée une seule fois dans le code que vous avez fourni, à savoir lors de l'appel somme_iteratif(5).
b) Quelles sont les différentes valeurs de l'argument n ?
Réponse : Dans le code fourni, l'argument n prend une seule valeur, à savoir 5.
c) Combien il y a-t-il de valeurs renvoyées ?
Réponse : Une seule valeur est renvoyée par la fonction lorsqu'elle est appelée. Pour l'appel somme_iteratif(5), la valeur renvoyée est 15.
d) Comment est calculée la valeur renvoyée ?
Réponse :
La valeur renvoyée est la somme des entiers de 0 à n inclus. Cette somme est calculée de manière itérative en utilisant une boucle for. À chaque itération de la boucle, la variable total est augmentée de la valeur de l'itérateur nombre jusqu'à ce que l'itérateur atteigne la valeur de n. Une fois la boucle terminée, la somme totale est renvoyée.
2) Méthode récursive
Une fonction récursive est une fonction qui s'appelle elle-même.
def somme_recursif(n):
if n == 0:
return 0
else:
return n + somme_recursif(n-1)
somme_recursif(5)from tutor import tutor
def somme_recursif(n):
if n == 0:
return 0
else:
return n + somme_recursif(n-1)
somme_recursif(5)
tutor()a) Combien de fois la fonction somme_recursif est-elle exécutée ?
Réponse : La fonction somme_recursif est exécutée 6 fois.
b) Quelles sont les différentes valeurs de l'argument n ?
Réponse : Les différentes valeurs de l'argument n sont 5, 4, 3, 2, 1 et 0.
c) Combien il y a-t-il de valeurs renvoyées ?
Réponse : Il y a 6 valeurs renvoyées, une pour chaque appel récursif de la fonction.
d) Laquelle (ou lesquelles) ?
Réponse : Les valeurs renvoyées sont 0, 1, 3, 6, 10 et 15.
3) Vérification de la Correction des Algorithmes Récursifs
Note : La section suivante peut être approfondie ultérieurement.
Pour prouver qu’un algorithme récursif fonctionne on doit prouver qu’il vérifie deux propriétés :
-
la Correction : si l’algorithme se termine, il doit renvoyer ce que l’on souhaite. Et aussi, il faut montrer que si les appels internes renvoient la bonne valeur, alors la fonction aussi.
-
la Terminaison : l’algorithme doit se terminer.
La logique sous-jacente à cette vérification est analogique à celle utilisée dans une preuve par récurrence en mathématiques.
def somme_recursif(n):
if n == 0:
return 0
else:
return n + somme_recursif(n-1)
somme_recursif(5)Correction :
— Initialisation (cas de base) :
pour n = 0 on a bien somme_recursif(0)= 0
et la premier valeur de la somme des entier est aussi 0
— Conservation : Suppose que pour n fixé les appels internes récursifs sont valides soit : somme_recursif(n) = 0 + 1 + ... + n alors puisque notre relation de récurrence est : somme_recursif(n) = n +somme_recursif(n − 1) donc somme_recursif(n+1) = (n+1) + somme_recursif(n) = 0 + 1 + ... + n + (n+1) On obtient bien notre hypothèse de récurrence.
Terminaison :
L’algorithme se termine car à chaque tour de boucle n diminue de 1 et on fini par arriver au cas n = 0.
Conclusion :
Les propriétés de correction et de terminaison sont juste, donc l'algorithme récursif fonctionne.
4) Temps d'exécution d'un fonction itérative et récursive
On peut comparer le temps d'exécution des deux fonctions précédentes grâce au module timeit.
from timeit import timeit
n = 100
duree_execution_iteratif = timeit(lambda:somme_iteratif(n), number=100)
print(duree_execution_iteratif)
duree_execution_recursif = timeit(lambda:somme_recursif(n), number=100)
print(duree_execution_recursif)0.0010000000002037268 0.005000000001018634
Augmentez la valeur de n.
a) Quelle est la version la plus rapide ?
Réponse : La fonction somme_iteratif
b) Que se passe-t-il si n est trop grand ?
Réponse : Seulement la fonction somme_iteratif marche .
c) Quelle est l'erreur rencontrée ?
Réponse : RecursionError: maximum recursion depth exceeded in comparison
Exercices :
Exercice 1 :
Factorielle est une opération mathématique notée avec un point d'exclamation : n!. On dira « factorielle n » ou « n factoriel ». La factorielle d'un entier naturel n est le produit des nombres entiers strictement positifs inférieurs ou égaux à n. Par convention 0! = 1.
On a donc 1! = 1, 2! = 2 x 1 = 2, 3! = 3 x 2 x 1 = 6,…
a) Proposez une fonction itérative en Python qui permette de calculer n!.
def factorielle(n):
f = 1
for i in range(n):
f = f * (i + 1)
return f
factorielle(4)b) Proposez une fonction récursive en Python qui permette de calculer n!.
def fact(n):
if n == 1:
return 1
else:
return n * fact(n - 1)
fact(4)Exercice 2 :
$$(u_n):\begin{cases}u_0 = 0 \ u_1=1\\forall n\in\mathbf N, u_{n+2}=u_{n+1}+u_n\end{cases}$$
a) Calculer le terme $u_{5}$.
$u_{5}$ = $u_{4}$ + $u_{3}$
$u_{4}$ = $u_{3}$ + $u_{2}$
$u_{3}$ = $u_{2}$ + $u_{1}$
$u_{2}$ = $u_{1}$ + $u_{0}$
donc
$u_{2}$ = 1 + 0 = 1
$u_{3}$ = 1 + 1 = 2
$u_{4}$ = 2 + 1 = 3
$u_{5}$ = 3 + 2 = 5
b) Écrivez une fonction itérative Fibonacci qui donnera le n ième terme de la suite de Fibonacci pour n>1.
def fibonacci(n):
a, b = 0, 1
for _ in range(2, n+1):
a, b = b, a + b
return b
fibonacci(5)c) Écrivez une fonction récursive Fibonacci qui donnera le n ième terme de la suite de Fibonacci pour n>1.
def Fibonacci(n):
if n < 2:
return n
else:
return Fibonacci(n-1) + Fibonacci(n-2)
Fibonacci(5)Exercice 3 :
L'algorithme d'Euclide permet de déterminer le plus grand diviseur commun à deux entiers naturels a et b avec a > b.
Il repose sur la propriété suivante :
- si b est non nul, on a PGCD(a,b)=PGCD(b,r) où r est le reste de la division entière de a par b.
- si b est nul, PGCD(a,b)=a
a. Proposer une formulation itérative de cet algorithme
def pgcd(a, b):
while b != 0:
a, b = b, a % b
return a
# Exemple d'utilisation
a = 56
b = 98
print(f"PGCD({a}, {b}) =", pgcd(a, b))PGCD(56, 98) = 14
b. Proposer une formulation récursive de cet algorithme.
def pgcd(a, b):
if b == 0:
return a
else:
return pgcd(b, a % b)
# Exemple d'utilisation
a = 56
b = 98
print(f"PGCD({a}, {b}) =", pgcd(a, b))PGCD(56, 98) = 14
Exercice 4 : Flocon de Koch
Nous allons utiliser le module Python Turtle. Ce module permet de dessiner très simplement.
Étudiez le Wikibook consacré au module Turtle (wikibook Turtle) afin d'acquérir les bases de ce module.
Visionnez la vidéo consacrée au flocon de Koch : vidéo consacrée au flocon de Koch.
Proposer une formulation récursive du flocon de Koch.
from turtle import *
def koch(longueur, n):
if n == 0:
forward(longueur)
else:
koch(longueur/3, n-1)
left(60)
koch(longueur/3, n-1)
right(120)
koch(longueur/3, n-1)
left(60)
koch(longueur/3, n-1)
def flocon(taille, etape):
koch(taille, etape)
right(120)
koch(taille, etape)
right(120)
koch(taille, etape)
flocon(100, 3)Exercice 5 : Tour de Hanoï
Voir Hanoï sur la page d'accueil
Bilan sur la récursivité
La récursivité est généralement plus simple à programmer une fois qu'on a trouvé la bonne relation de récursion. Par contre la consommation mémoire est généralement plus importante que pour la programmation itérative.
4.3 - Modularité
Langages et programmation
Modularité
Conpétences exigibles :
Utiliser des API (Application Programming Interface) ou des bibliothèques.
Exploiter leur documentation.
Créer des modules simples et les documenter.
1. Qu'est-ce que la modularité?
La modularité est une stratégie de conception qui décompose un système en modules distincts, où chaque module gère une fonctionnalité spécifique du système global. L'idée est de créer des pièces réutilisables qui peuvent être assemblées de différentes manières pour créer des systèmes variés.
Avantages de la modularité :
- Réutilisabilité: Les modules peuvent être réutilisés dans différents projets.
- Maintenabilité: Les erreurs peuvent être isolées à un module, ce qui facilite la localisation et la résolution des problèmes.
- Extensibilité: Il est plus facile d'ajouter, de retirer ou de modifier des fonctionnalités.
- Compréhensibilité: En décomposant un système complexe en modules plus petits, il est plus facile à comprendre.
Comment appliquer la modularité?
Fonctions: C'est la forme la plus basique de modularité. Une fonction encapsule un bloc de code qui effectue une tâche spécifique.
Classes et objets: Dans la programmation orientée objet, les classes peuvent être vues comme des modules. Une classe encapsule des données (attributs) et des méthodes pour manipuler ces données.
Bibliothèques et Frameworks: Ce sont des collections de fonctions, de classes et d'autres ressources que les développeurs peuvent utiliser pour éviter de "réinventer la roue".
Exemple de langages supportant la modularité:
- Python: Python supporte la modularité à travers des fonctions, des classes, et des modules (fichiers .py qui peuvent être importés dans d'autres scripts).
- Java: Java utilise des classes et des packages pour gérer la modularité.
- JavaScript (ES6 et supérieur): Supporte l'importation et l'exportation de modules.
Bonnes pratiques en matière de modularité:
- Cohésion: Assurez-vous que chaque module a une responsabilité claire et bien définie.
- Faible couplage: Les modules doivent être aussi indépendants que possible les uns des autres.
- Documentation: Documentez l'objectif, les entrées, les sorties et les comportements de chaque module.
- Tests: Chaque module doit avoir ses propres tests pour garantir qu'il fonctionne comme prévu.
2. Les modules Python
Pour vraiment maîtriser l'utilisation des modules en Python, il est essentiel de savoir comment accéder aux informations sur ce qu'ils contiennent et comment ils fonctionnent.
Liste des fonctions et classes d'un module:
Après avoir importé un module, vous pouvez utiliser la fonction dir() pour lister tous ses attributs, fonctions, et classes:
import math
print(dir(math))['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'expm1', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
Cela vous donne une liste de toutes les fonctions et constantes disponibles dans le module math.
Utiliser l'aide:
La fonction help() est intégrée à Python et permet d'afficher la documentation d'une fonction, classe ou module:
import math
help(math.sqrt)Help on built-in function sqrt in module math:
sqrt(x, /)
Return the square root of x.
Cela affiche une explication sur la fonction sqrt() du module math.
Accéder à la documentation (docstrings):
La plupart des fonctions, classes, et modules en Python contiennent des chaînes de documentation, ou docstrings, qui fournissent une explication concise de leur utilité et de leur utilisation. Vous pouvez y accéder en utilisant l'attribut doc:
print(math.cos.__doc__)Return the cosine of x (measured in radians).
Cela affichera la docstring pour la fonction cos().
Lorsque vous travaillez avec des packages tiers (ceux que vous installez via pip, par exemple), la documentation officielle ou la page GitHub du package est souvent le meilleur endroit pour trouver des informations. Les grands packages tels que NumPy, pandas ou Flask ont des documentations complètes disponibles en ligne.
Des environnements de développement intégrés (IDE) comme PyCharm, Visual Studio Code (avec l'extension Python), et autres offrent souvent des fonctionnalités d'introspection qui permettent de voir rapidement la documentation ou la signature d'une fonction en passant simplement la souris dessus ou en appuyant sur une combinaison de touches.
Si vous avez besoin d'une compréhension plus profonde de la manière dont un module ou une fonction fonctionne, et que la documentation ne suffit pas, vous pouvez souvent consulter directement le code source. Pour les modules de la bibliothèque standard ou les packages installés via pip, vous pouvez généralement trouver le code source sur GitHub ou d'autres plateformes de gestion de code source.
3. Les déclarations import en Python
Les déclarations import en Python sont utilisées pour accéder aux fonctions, classes, variables et autres éléments d'un module. Je vais décomposer chaque forme d'importation.
3.1 import
La déclaration import est utilisée pour importer un module entier.
Après avoir exécuté l'instruction ci-dessous, vous pouvez accéder à toutes les fonctions et variables définies dans le module math en utilisant la notation pointée. Par exemple, math.sqrt(2) renverrait 1.4142135623730951.
import math
math.sqrt(2)3.2 from ... import ...
La déclaration from ... import ... est utilisée pour importer des éléments spécifiques (comme des fonctions, des classes ou des variables) d'un module.
Avec cette forme d'importation, vous n'avez plus besoin d'utiliser la notation pointée pour accéder à la fonction sqrt. Vous pouvez simplement écrire sqrt(2).
from math import sqrt
sqrt(2)3.3 from ... import *
La déclaration from ... import * importe tous les éléments d'un module directement dans l'espace de noms courant. Cela signifie que vous n'aurez pas à utiliser la notation pointée pour accéder à ces éléments. Après cette instruction, vous pouvez directement utiliser des fonctions comme sqrt, sin, cos, etc., sans préfixe.
from math import *
sqrt(2)Attention : Bien que cette méthode d'importation puisse sembler pratique, elle est généralement déconseillée car elle peut rendre le code moins lisible (il devient plus difficile de déterminer d'où proviennent certaines fonctions ou variables) et peut causer des conflits si deux modules importés ont des fonctions ou des variables avec le même nom.
3.4 from module_name import element_name as alias
Vous pouvez également attribuer un alias à des éléments spécifiques lors de leur importation.
from math import sqrt as racine_carree
racine_carree(2)3.5 import module_name as alias
Lorsque vous importez un module entier, vous pouvez lui attribuer un alias pour rendre votre code plus concis ou pour éviter des conflits de noms.
import numpy
A = numpy.array([[1, 2], [3, 4]])
print(A)[[1 2] [3 4]]
import numpy as np
A = np.array([[1, 2], [3, 4]])
print(A)[[1 2] [3 4]]
4. Créer un module avec un autre programme Python
Supposons que nous voulions développer un petit système pour gérer les opérations mathématiques basiques comme l'addition, la soustraction, la multiplication, et la division.
Nous pouvons diviser chaque opération mathématique en un module distinct. Pour simplifier, nous les garderons dans un seul fichier, mais dans de grands projets, chaque module pourrait être dans un fichier séparé.
# operations.py
def addition(a, b):
return a + b
def soustraction(a, b):
return a - b
def multiplication(a, b):
return a * b
def division(a, b):
if b == 0:
return "Erreur: Division par zéro!"
return a / bMaintenant, nous allons créer un fichier principal (main.py) qui importera et utilisera notre module operations.py.
# main.py
import operations
a = 10
b = 5
print(f"{a} + {b} = {operations.addition(a, b)}")
print(f"{a} - {b} = {operations.soustraction(a, b)}")
print(f"{a} * {b} = {operations.multiplication(a, b)}")
print(f"{a} / {b} = {operations.division(a, b)}")
Lorsque vous exécutez main.py, vous obtiendrez le résultat des opérations.
Avantages de cette approche
- Réutilisabilité: Si nous avons besoin d'effectuer ces opérations mathématiques dans un autre projet, nous pouvons simplement copier le fichier operations.py sans avoir besoin de réécrire le code.
- Maintenabilité: Si nous devons modifier la manière dont une opération fonctionne, nous n'avons qu'à le faire dans le module operations.py sans affecter le reste du code.
- arté: En séparant les fonctionnalités en modules, il est plus facile pour d'autres développeurs (ou pour vous-même dans le futur) de comprendre le code et de savoir où chercher pour des fonctionnalités spécifiques.
Cet exemple est simpliste, mais il montre le concept de base de la modularité en Python. Dans des projets réels, vous auriez probablement des modules plus complexes, et vous pourriez utiliser des packages pour organiser ces modules en groupes logiques.
5. La Programmation Orientée Objet (POO)
La Programmation Orientée Objet (POO) est une approche de la programmation qui regroupe les données et les fonctions qui opèrent sur ces données en une seule entité, appelée objet. Elle est basée sur quelques concepts clés que nous allons explorer.
Concepts clés de la POO:
-
Classe: C'est le plan ou la définition pour la création d'un objet. Une classe définit les attributs et les méthodes qui caractériseront chaque objet créé à partir de cette classe.
-
Objet: Une instance d'une classe. Il représente une entité concrète qui est construite selon la définition de sa classe.
-
Encapsulation: Cela signifie que l'état interne d'un objet est caché de l'extérieur. Seules les méthodes de l'objet peuvent accéder à son état interne.
-
Héritage: Permet à une classe d'hériter des attributs et méthodes d'une autre classe.
-
Polymorphisme: La capacité d'une classe à être traitée comme une instance d'une autre classe ou d'une interface.
POO en Python:
En Python, tout est un objet. Même les types de base comme les entiers, les chaînes et les listes sont des objets avec leurs propres méthodes.
Exemple simple de classe et d'objet en Python:
La Programmation Orientée Objet (POO) est une approche de la programmation qui regroupe les données et les fonctions qui opèrent sur ces données en une seule entité, appelée objet. Elle est basée sur quelques concepts clés que nous allons explorer.
Concepts clés de la POO:
-
Classe: C'est le plan ou la définition pour la création d'un objet. Une classe définit les attributs et les méthodes qui caractériseront chaque objet créé à partir de cette classe.
-
Objet: Une instance d'une classe. Il représente une entité concrète qui est construite selon la définition de sa classe.
-
Encapsulation: Cela signifie que l'état interne d'un objet est caché de l'extérieur. Seules les méthodes de l'objet peuvent accéder à son état interne.
-
Héritage: Permet à une classe d'hériter des attributs et méthodes d'une autre classe.
-
Polymorphisme: La capacité d'une classe à être traitée comme une instance d'une autre classe ou d'une interface.
POO en Python:
En Python, tout est un objet. Même les types de base comme les entiers, les chaînes et les listes sont des objets avec leurs propres méthodes.
# Classe
class Animal:
def __init__(self, nom, espece): # Le constructeur __init__ initialise l'objet lors de sa création
self.nom = nom # Attribut
self.__espece = espece # Attribut
def parler(self):
return f"Je suis {self.nom}, un(e) {self.__espece}"
# Objet
lion = Animal("Simba", "lion") # Création d'un objet "lion" de la classe Animal
print(lion.parler()) # Appel de la méthode parler() de l'objet lion
Je suis Simba, un(e) lion
Autre exemple :
class Vehicule:
def __init__(self, marque):
self.marque = marque
def afficher(self):
print(f"C'est un véhicule de marque {self.marque}")
class Moto(Vehicule):
def afficher_type(self):
print("C'est une moto")
ma_moto = Moto("Honda") # Création d'un objet "Honda" de la classe Moto
ma_moto.afficher_type()
ma_moto.afficher()C'est une moto C'est un véhicule de marque Honda
6. La création de documentation pour un module en Python
La création de documentation pour un module en Python repose généralement sur deux étapes :
- Écrire des docstrings: Ce sont des chaînes littérales qui apparaissent en haut des modules, classes, méthodes ou fonctions pour décrire ce qu'ils font.
- Utiliser un outil pour générer la documentation: À partir des docstrings, vous pouvez utiliser des outils pour générer une documentation au format HTML, PDF, etc.
Les docstrings sont entourés de triples guillemets (simples ou doubles). Voici un exemple de module avec des docstrings:
"""
Module pour gérer des opérations mathématiques basiques.
"""
def addition(a, b):
"""
Retourne la somme de a et b.
Args:
a (int ou float): Premier nombre.
b (int ou float): Deuxième nombre.
Returns:
int ou float: Somme de a et b.
"""
return a + b
L'outil le plus couramment utilisé pour générer une documentation à partir de docstrings est Sphinx. Installation de Sphinx: pip install sphinx Sphinx génére des fichiers HTML dans docs/build/html que vous pouvez ouvrir dans un navigateur pour voir la documentation.
N'oubliez pas de tenir vos docstrings à jour lorsque vous modifiez ou ajoutez du code à votre module. Une documentation précise et à jour est essentielle pour assurer la clarté et la maintenabilité de votre code.
4.4 - Paradigmes de programmation
Langages et programmation
Paradigmes de programmation
Capacités Attendue :
- Distinguer sur des exemples les paradigmes impératif, fonctionnel et objet.
- Choisir le paradigme de programmation selon le champ d’application d’un programme.
Commentaires :
Avec un même langage de programmation, on peut utiliser des paradigmes différents. Dans un même programme, on peut utiliser des paradigmes différents.
1. Paradigme Impératif
Dans le paradigme impératif, le programme est constitué d'une séquence d'instructions qui modifient l'état de la machine. Il est très similaire à la façon dont les humains accomplissent les tâches étape par étape.
Exemple en Python :
# Calcul de la somme de 1 à n
n = 10
somme = 0
for i in range(1, n+1):
somme += i
print("La somme est :", somme)La somme est : 55
2. Paradigme Fonctionnel
Le paradigme fonctionnel se concentre sur l'évaluation des fonctions. Il évite de modifier l'état et de manipuler des données. En général, les fonctions sont "pures", c'est-à-dire qu'elles donnent toujours la même sortie pour une entrée donnée et n'ont pas d'effets secondaires.
Exemple en Python :
# Calcul de la somme de 1 à n en utilisant une approche fonctionnelle
def somme_recursive(n):
if n == 0:
return 0
else:
return n + somme_recursive(n-1)
print("La somme est :", somme_recursive(10))La somme est : 55
3. Paradigme Orienté Objet (POO)
Dans le paradigme orienté objet, le programme est constitué d'objets qui contiennent à la fois des données et des méthodes pour manipuler ces données. Le but est de regrouper les données et les fonctions qui les manipulent afin de faciliter la conception, l'organisation et la maintenance du code.
Exemple en Python :
# Classe pour calculer la somme de 1 à n
class Somme:
def __init__(self, n):
self.n = n
def calculer(self):
somme = 0
for i in range(1, self.n + 1):
somme += i
return somme
s = Somme(10)
print("La somme est :", s.calculer())La somme est : 55
4. Choisir le Paradigme Selon le Champ d'Application
- Impératif: Utilisé couramment pour des applications à faible niveau où les performances sont cruciales.
- Fonctionnel: Utilisé en mathématiques, en traitement de données, en parallélisation, etc.
- Orienté Objet: Utilisé dans les applications d'entreprise, les systèmes de gestion de bases de données, les interfaces graphiques, etc.
5. Utilisation de Paradigmes Différents dans un Même Programme
Un langage de programmation polyvalent comme Python permet aux développeurs d'utiliser différents paradigmes de programmation pour résoudre différents problèmes. Par exemple, vous pourriez utiliser une approche impérative pour une tâche qui nécessite un contrôle étroit du flux du programme, tout en utilisant une approche orientée objet pour structurer votre code autour d'entités complexes.
Il est également possible d'utiliser plusieurs paradigmes dans un seul et même programme. Voici un exemple simple en Python qui combine les paradigmes impératif, fonctionnel et orienté objet :
# Fonction fonctionnelle pour calculer la somme d'une liste
def somme_liste(lst):
if len(lst) == 0:
return 0
else:
return lst[0] + somme_liste(lst[1:])
# Classe pour représenter un étudiant (Orienté Objet)
class Etudiant:
def __init__(self, nom, notes):
self.nom = nom
self.notes = notes
# Méthode pour calculer la note moyenne (Impératif)
def note_moyenne(self):
total = 0
for note in self.notes:
total += note
return total / len(self.notes)
# Méthode pour calculer la note moyenne en utilisant la fonction fonctionnelle (Fonctionnel)
def note_moyenne_fonctionnelle(self):
total = somme_liste(self.notes)
return total / len(self.notes)
# Création d'un objet Etudiant
etudiant = Etudiant("Alice", [90, 85, 77, 92])
# Utilisation d'une méthode impérative
print(f"Note moyenne (Impératif): {etudiant.note_moyenne()}")
# Utilisation d'une méthode fonctionnelle
print(f"Note moyenne (Fonctionnel): {etudiant.note_moyenne_fonctionnelle()}")Note moyenne (Impératif): 86.0 Note moyenne (Fonctionnel): 86.0
Dans cet exemple, la classe Etudiant utilise une méthode impérative (note_moyenne) pour calculer la note moyenne en utilisant une boucle for. Par ailleurs, elle utilise également une méthode fonctionnelle (note_moyenne_fonctionnelle) qui fait appel à la fonction somme_liste, une fonction écrite dans le style fonctionnel.
Ainsi, différents paradigmes peuvent coexister dans un même programme pour résoudre différents problèmes, chacun d'une manière qui est le plus naturel ou efficace pour ce problème spécifique.

4.5 - Gestion des bugs
Langages et programmation
Mise au point des programmes. Gestion des bugs.
Capacités Attendue :
Dans la pratique de la programmation, savoir répondre aux causes typiques de bugs : problèmes liés au typage, effets de bord non désirés, débordements dans les tableaux, instruction conditionnelle non exhaustive, choix des inégalités, comparaisons et calculs entre flottants, mauvais nommage des variables, etc.
Commentaires :
- On prolonge le travail entrepris en classe de première sur l’utilisation de la spécification, des assertions,de la documentation des programmes et de la construction de jeux de tests.
- Les élèves apprennent progressivement à anticiper leurs erreurs.
1. Erreurs les plus courantes en Python
Lors de l'écriture de code Python, les erreurs sont «gentiment» rappelées par l'interpréteur Python à l'exécution du code.
Type d'erreur | Objet Python | Erreurs courantes | Exemple |
Erreur de syntaxe |
| Erreur de parenthèse, : manquant avant un bloc d'instruction.... |
|
Erreurs d'indexation |
| Accès à un index non présent dans une liste. Accès à un index non présent dans une liste, ou un tuple, str... |
|
Erreurs de nom |
| Nom de fonction ou de variable mal orthographié. |
|
Erreurs d'indentation |
| Indentation oubliée, ou trop grande, les blocs sont alors mal délimités. | |
Erreurs de type |
| Opération impossible entre deux types(str - int). Conversion de type impossible. |
|
En général, ces erreurs nécessitent de modifier le code pour corriger le «bug».
2. Tour d'horizon des bonnes pratiques de programmation
Pour développer et mettre au point un programme, il vous faudra :
- Repérer les "bugs" courants : problèmes de syntaxe, d'indentation, de parenthèses ou guillemets oubliés, portée locale ou globale des variables,...
- Anticiper et gérer les erreurs de saisie de l'utilisateur
- Utiliser les mécanismes d'assertions pour s'assurer de la bonne exécution du programme en toute circonstance en créant des jeux de tests
- Vérifier les boucles : s'assurer que la condition de fin de boucle sera bien atteinte
- Les nombres flottants : anticiper les problèmes liés à la représentation approchée de leur valeur
- Les listes : être attentif aux indices
- Problèmes liés au typage
- Nommer de façon cliare les noms des variables pour rendre le code facile à comprendre et à déboguer.
- faire attention au instructions conditionnelles non exhaustives un if-else qui ne couvre pas tous les cas possibles.
- Ne pas attendre de taper votre programme complétement, tester des régulièrement votre programme durant la création
- ...
# Erreur de syntaxe, parenthèse fermante manquante
print("Hello, world" # Erreur d'indentation
def ma_fonction():
print("Indentation incorrecte")# Erreur de guillemets
print('J'ai fain')# Utiliser les mécanismes d'assertions pour s'assurer de la bonne exécution du programme
def diviser(a, b):
assert b != 0, "Division par zéro impossible" #
return a / b
result = diviser(10, 0) # Déclenche une AssertionError# Vérifier les boucles
n = 5
while n > 0:
print(n)
n += 1⚠ ∞ !!!!!!!!!!!!!# Résultat imprévisible en raison de la représentation des nombres flottants
a = 0.1 + 0.1 + 0.1
b = 0.3
print(a == b)# IndexError : L'indice 5 est hors de la plage valide
ma_liste = [1, 2, 3, 4, 5]
print(ma_liste[5])# Problèmes liés au typage
x = "42"
y = x + 104. Construction de Jeux de Tests :
Pour anticiper les erreurs, il est essentiel de créer des jeux de tests complets qui couvrent divers scénarios d'utilisation du programme. Les tests unitaires, les tests d'intégration et les tests de validation sont tous importants..
Trouver les erreurs ci-dessous :
def ajouter(a, b):
"""
Cette fonction ajoute deux nombres.
:param a: Premier nombre
:param b: Deuxième nombre
:return: La somme de a et b
"""
assert isinstance(a, int), "a doit être un nombre entier"
assert isinstance(b, (int, float)), "b doit être un nombre"
return a + b
# Jeu de tests
assert ajouter(1, 2) == 3
assert ajouter(-1.5, 1) == -0.5
assert ajouter(0, 0) == 0
5. try...except
Parfois ces erreurs "sont prévues" et nécessitent d'être gérées sans arrêter complètement le programme.
Gestion des exceptions avec try : ... except ...
Prenons l'exemple de la gestion d'une entrée utilisateur (on a dit qu'"« il fallait s'attendre à tout ... »")
Vous demandez l'âge d'une personne et vous attendez un entier pour vérifier son accès.
Il faut lui reposer la question jusqu'à ce qu'il rentre une valeur conforme à nos attentes.
try:
nombre = int("abc") # Cela va lever une ValueError car "abc" ne peut pas être converti en int.
except ValueError as erreur:
print("Une erreur de valeur est survenue :", erreur)# Anticiper et gérer les erreurs de saisie de l'utilisateur
try:
num = int(input("Entrez un nombre : "))
print("Vous avez saisi :", num)
except ValueError:
print("Erreur : Veuillez entrer un nombre valide.") age = None
while not age:
try:
age = int(input("Quel âge avez-vous? "))
except ValueError:
print("Veuillez entrer votre âge sous forme de chiffres")
# on est sur d'avoir un age entier ici
if age >= 13:
print("Vous pouvez vous inscrire")
else:
print("Les réseaux sociaux sont interdits aux moins de 13 ans.")try:
# Tentative d'ouverture d'un fichier non-existant
f = open('non_existent_file.txt', 'r')
except IOError:
# Ce bloc sera exécuté si l'ouverture du fichier échoue
print('Erreur: Le fichier ne peut pas être trouvé ou lu.')


5.1 - Algorithme Graphes
Algorithmique
Algorithmes sur les graphes
Capacités Attendue :
- Parcourir un graphe en profondeur d’abord, en largeur d’abord.
- Repérer la présence d’un cycle dans un graphe.
- Chercher un chemin dans un graphe.
Commentaires :
- Le parcours d’un labyrinthe et le routage dans Internet sont des exemples d’algorithme sur les graphes.
- L’exemple des graphes permet d’illustrer l’utilisation des classes en programmation.
0. Rappels :
import numpy as np
import networkx as nx # nécessaire pour afficher le graphe
import matplotlib.pyplot as plt # nécessaire pour afficher le graphe
class Graphe_Matrice_Adjacente:
def __init__(self, matrice_adjacence, noms_sommets):
self.matrice_adjacence = matrice_adjacence
self.noms_sommets = noms_sommets
def liste_successeurs(self):
liste_succ = {}
n = len(self.matrice_adjacence)
for i in range(n):
successeurs = []
for j in range(n):
if self.matrice_adjacence[i][j]:
successeurs.append(self.noms_sommets[j])
liste_succ[self.noms_sommets[i]] = successeurs
return liste_succ
def liste_predecesseurs(self):
liste_pred = {}
n = len(self.matrice_adjacence)
for j in range(n):
predecesseurs = []
for i in range(n):
if self.matrice_adjacence[i][j]:
predecesseurs.append(self.noms_sommets[i])
liste_pred[self.noms_sommets[j]] = predecesseurs
return liste_pred
def afficher(self, figsize=(6, 6)): # n'est pas demandé dans le cours de NSI
plt.figure(figsize=figsize)
G = nx.DiGraph()
edge_labels = {}
for i, nom_sommet in enumerate(self.noms_sommets):
for j, poids in enumerate(self.matrice_adjacence[i]):
if poids != 0:
G.add_edge(nom_sommet, self.noms_sommets[j], weight=poids)
edge_labels[(nom_sommet, self.noms_sommets[j])] = poids
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, font_weight='bold', node_color='skyblue', font_size=12, node_size=500, arrows=True)
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
plt.show()
matrice_adjacence = [
[0, 2, 1, 3, 0, 0, 0, 0], # A
[2, 0, 0, 0, 1, 3, 0, 0], # B
[1, 0, 0, 0, 0, 0, 3, 2], # C
[3, 0, 0, 0, 0, 0, 0, 0], # D
[0, 1, 0, 0, 0, 0, 0, 0], # E
[0, 3, 0, 0, 0, 0, 0, 0], # F
[0, 0, 3, 0, 0, 0, 0, 1], # G
[0, 0, 2, 0, 0, 0, 1, 0], # H
]
noms_sommets = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
graphe = Graphe_Matrice_Adjacente(matrice_adjacence, noms_sommets)
graphe.afficher()
dictionnaire_successeurs = graphe.liste_successeurs()
dictionnaire_predecesseur = graphe.liste_predecesseurs()
print('Successeurs : ', dictionnaire_successeurs)
print('Prédécesseurs : ',dictionnaire_predecesseur)Successeurs : {'A': ['B', 'C', 'D'], 'B': ['A', 'E', 'F'], 'C': ['A', 'G', 'H'], 'D': ['A'], 'E': ['B'], 'F': ['B'], 'G': ['C', 'H'], 'H': ['C', 'G']}
Prédécesseurs : {'A': ['B', 'C', 'D'], 'B': ['A', 'E', 'F'], 'C': ['A', 'G', 'H'], 'D': ['A'], 'E': ['B'], 'F': ['B'], 'G': ['C', 'H'], 'H': ['C', 'G']}
1. DFS et BFS
DFS est l'acronyme de Depth-First Search, qui se traduit en français par Parcours en profondeur d'abord.
Le parcours DFS est un parcours où on va aller «le plus loin possible» sans se préoccuper des autres voisins non visités, ni des poids des arêtes : on va visiter le premier de ses voisins non traités, qui va faire de même, etc. Lorsqu'il n'y a plus de voisin, on revient en arrière pour aller voir le dernier voisin non visité.
BFS est l'acronyme de Breadth-First Search, qui se traduit en français par Parcours en Largeur.
le parcours BFS en selectionnant un nœud et il explore tous les nœuds voisins avant de passer aux nœuds au niveau suivant, indépendamment des poids des arêtes. Un parcours BFS peut donc trouver le plus court chemin entre 2 nœuds, mais en prenant des poids de 1 pour les arêtes.
def DFS(graph,debut):
result = []
a_visite = [debut]
while a_visite:
noeux=a_visite.pop(0)
if noeux not in result:
result.append(noeux)
a_visite = graph[noeux] + a_visite
return result
def BFS(graph,debut):
result = []
a_visite = [debut]
while a_visite:
noeux = a_visite.pop(0)
if noeux not in result:
result.append(noeux)
a_visite = a_visite + graph[noeux]
return result
# Exemple de graphe
graph_successeurs = {'A': ['B', 'C', 'D'],
'B': ['A', 'E', 'F'],
'C': ['A', 'G', 'H'],
'D': ['A'],
'E': ['B'],
'F': ['B'],
'G': ['C', 'H'],
'H': ['C', 'G']}
# Lancer la recherche en profondeur à partir de 'A'
resultat = DFS(graph_successeurs, 'A')
print("Ordre de visite DFS :", resultat)
# Lancer le parcours en largeur à partir de 'A'
resultat = BFS(graph_successeurs, 'A')
print("Ordre de visite BFS :", resultat)Ordre de visite DFS : ['A', 'B', 'E', 'F', 'C', 'G', 'H', 'D'] Ordre de visite BFS : ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
2. Labyrinthe ou chemin
Dans le contexte d'un labyrinthe, le BFS pour trouve le chemin le plus court (poids = 1) entre le point de départ et le point d'arrivée.
def chemin(graphe, depart, arrivee):
file = [([depart], [])] # La file contient des tuples de chemin et de liste d'arêtes utilisées
chemins = []
while file:
chemin_actuel, aretes_utilisees = file.pop(0)
noeud_actuel = chemin_actuel[-1]
if noeud_actuel == arrivee and len(chemin_actuel) > 1:
chemins.append(chemin_actuel)
continue
for voisin in graphe.get(noeud_actuel, []):
arete = (noeud_actuel, voisin)
if arete not in aretes_utilisees: # Vérifie si l'arête a déjà été utilisée
nouvelles_aretes = aretes_utilisees + [arete, (voisin, noeud_actuel)] # Ajoute l'arête dans les deux sens
nouveau_chemin = chemin_actuel + [voisin]
file.append((nouveau_chemin, nouvelles_aretes))
if chemins:
print(f"Listes de tous les chemins trouvé(s) de {depart} vers {arrivee} :")
for chemin in chemins:
print(f" - {chemin}")
else:
print(f"Aucun chemin de {depart} vers {arrivee} trouvé!")
# Exemples
graph_successeurs = {'A': ['B', 'C', 'D'],
'B': ['A', 'E', 'F'],
'C': ['A', 'G', 'H'],
'D': ['A'],
'E': ['B'],
'F': ['B'],
'G': ['C', 'H'],
'H': ['C', 'G']}
chemin(graph_successeurs, 'G', 'F')
chemin(graph_successeurs, 'C', 'C')Listes de tous les chemins trouvé(s) de G vers F : - ['G', 'C', 'A', 'B', 'F'] - ['G', 'H', 'C', 'A', 'B', 'F'] Listes de tous les chemins trouvé(s) de C vers C : - ['C', 'G', 'H', 'C'] - ['C', 'H', 'G', 'C']
3. Détection d'un cycle
# Exemples
graph_successeurs = {'A': ['B', 'C', 'D'],
'B': ['A', 'E', 'F'],
'C': ['A', 'G', 'H'],
'D': ['A'],
'E': ['B'],
'F': ['B'],
'G': ['C', 'H'],
'H': ['C', 'G']}
chemin(graph_successeurs, 'D','D')
chemin(graph_successeurs, 'C','C')Aucun chemin de D vers D trouvé! Listes de tous les chemins trouvé(s) de C vers C : - ['C', 'G', 'H', 'C'] - ['C', 'H', 'G', 'C']
4. Algorithme de Dijkstra

Edsger Wybe Dijkstra né à Rotterdam le 11 mai 1930 et mort2 à Nuenen le 6 août 2002, est un mathématicien et informaticien néerlandais du XXe siècle. Il reçoit en 1972 le prix Turing pour ses contributions sur la science et l’art des langages de programmation et au langage Algol. Juste avant sa mort, en 2002, il reçoit le prix PoDC de l'article influent, pour ses travaux sur l'autostabilisation. L'année suivant sa mort, le prix sera renommé en son honneur prix Dijkstra.
Exemple : Dijkstra
# Algorithme de Dijkstra orienté avec poids
import networkx as nx
import matplotlib.pyplot as plt
import pandas as pd
class GrapheOrienteAvecPoids:
def __init__(self, liste_sommets):
self.liste_sommets = liste_sommets
self.adjacents = {sommet: {} for sommet in liste_sommets}
def ajoute_arete(self, sommetA, sommetB, poids):
self.adjacents[sommetA][sommetB] = poids
def voisins(self, sommet):
return self.adjacents[sommet]
def sont_voisins(self, sommetA, sommetB):
return sommetB in self.adjacents[sommetA]
def poids(self, sommetA, sommetB):
return self.adjacents[sommetA].get(sommetB, None)
def matrice_adjacente(self):
matrice = []
for sommetA in self.liste_sommets:
ligne = []
for sommetB in self.liste_sommets:
ligne.append(self.poids(sommetA, sommetB) if self.sont_voisins(sommetA, sommetB) else 0)
matrice.append(ligne)
return matrice
def liste_successeurs(self):
return {sommet: list(self.voisins(sommet).keys()) for sommet in self.liste_sommets}
def liste_predecesseurs(self):
predecesseurs = {sommet: [] for sommet in self.liste_sommets}
for sommet in self.liste_sommets:
for voisin in self.voisins(sommet):
predecesseurs[voisin].append(sommet)
return predecesseurs
def nombre_aretes_par_sommet(self):
degres_sortants = {sommet: len(self.voisins(sommet)) for sommet in self.liste_sommets}
degres_entrants = {sommet: 0 for sommet in self.liste_sommets}
for sommet in self.liste_sommets:
for voisin in self.voisins(sommet):
degres_entrants[voisin] += 1
return {"degres_sortants": degres_sortants, "degres_entrants": degres_entrants}
def dessiner(self, figsize=(6, 6)):
plt.figure(figsize=figsize)
G = nx.DiGraph()
for sommet, voisins in self.adjacents.items():
for voisin, poids in voisins.items():
G.add_edge(sommet, voisin, weight=poids)
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, font_weight='bold', node_color='skyblue', font_size=12, node_size=500, font_color='black')
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)
plt.show()
def dijkstra_tableau(self, debut, fin=None):
distances = {sommet: float('infinity') for sommet in self.liste_sommets}
predecesseurs = {sommet: None for sommet in self.liste_sommets}
distances[debut] = 0
selectionnes = set()
tableau = pd.DataFrame(columns=self.liste_sommets + ['Choix'])
while len(selectionnes) < len(self.liste_sommets):
non_selectionnes = {sommet: distances[sommet] for sommet in self.liste_sommets if sommet not in selectionnes}
sommet_courant = min(non_selectionnes, key=non_selectionnes.get)
if fin is not None and sommet_courant == fin:
break
for voisin, poids in self.voisins(sommet_courant).items():
if distances[voisin] > distances[sommet_courant] + poids:
distances[voisin] = distances[sommet_courant] + poids
predecesseurs[voisin] = sommet_courant
selectionnes.add(sommet_courant)
ligne_actuelle = [f"X" if sommet in selectionnes else f"{distances[sommet]}v{predecesseurs[sommet]}" if distances[sommet] != float('infinity') else "∞" for sommet in self.liste_sommets]
ligne_actuelle.append(f"{sommet_courant}({distances[sommet_courant]})")
tableau = pd.concat([tableau, pd.DataFrame([ligne_actuelle], columns=tableau.columns)], ignore_index=True)
return tableau, self.calcule_chemin(predecesseurs, debut, fin)
def calcule_chemin(self, predecesseurs, debut, fin):
chemin = []
sommet_actuel = fin
while sommet_actuel and sommet_actuel != debut:
chemin.append(sommet_actuel)
sommet_actuel = predecesseurs[sommet_actuel]
if sommet_actuel:
chemin.append(debut)
chemin.reverse()
distance = sum([self.poids(chemin[i], chemin[i + 1]) for i in range(len(chemin) - 1)]) if chemin else float('infinity')
return chemin, distance
def format_chemin(chemin):
return " → ".join(chemin)
g = GrapheOrienteAvecPoids(['A', 'B', 'C', 'D', 'E', 'F'])
g.ajoute_arete('A', 'B', 8)
g.ajoute_arete('A', 'E', 3)
g.ajoute_arete('B', 'A', 7)
g.ajoute_arete('B', 'F', 10)
g.ajoute_arete('B', 'C', 7)
g.ajoute_arete('C', 'B', 6)
g.ajoute_arete('C', 'D', 10)
g.ajoute_arete('D', 'A', 12)
g.ajoute_arete('D', 'F', 3)
g.ajoute_arete('E', 'D', 11)
g.ajoute_arete('E', 'B', 6)
g.ajoute_arete('F', 'E', 11)
g.ajoute_arete('F', 'C', 1)
g.dessiner()
tableau_dijkstra, chemin_info = g.dijkstra_tableau('A', 'F')
print(tableau_dijkstra)
print()
print("Chemin le plus court", format_chemin(chemin_info[0]), "de distance", chemin_info[1])A B C D E F Choix 0 X 8vA ∞ ∞ 3vA ∞ A(0) 1 X 8vA ∞ 14vE X ∞ E(3) 2 X X 15vB 14vE X 18vB B(8) 3 X X 15vB X X 17vD D(14) 4 X X X X X 17vD C(15) Chemin le plus court A → E → D → F de distance 17
# Création du graphe avec les sommets
graphe = GrapheOrienteAvecPoids(['Paris', 'Lyon', 'Marseille', 'Toulouse'])
# Ajout des arêtes directement avec leurs poids
graphe.ajoute_arete('Paris', 'Lyon', 465)
graphe.ajoute_arete('Lyon','Paris', 465)
graphe.ajoute_arete('Lyon', 'Marseille', 320)
graphe.ajoute_arete('Marseille','Lyon', 320)
graphe.ajoute_arete('Lyon', 'Toulouse', 537)
graphe.ajoute_arete('Toulouse','Lyon', 537)
graphe.ajoute_arete('Marseille', 'Toulouse', 403)
graphe.ajoute_arete('Toulouse', 'Marseille', 403)
# Dessin du graphe
graphe.dessiner()
# Utiliser l'algorithme de Dijkstra pour trouver le chemin le plus court de Paris à Marseille
tableau_dijkstra, chemin_info = graphe.dijkstra_tableau('Paris', 'Marseille')
print(tableau_dijkstra)
print()
print("Chemin le plus court", format_chemin(chemin_info[0]), "de distance", chemin_info[1])
Paris Lyon Marseille Toulouse Choix 0 X 465vParis ∞ ∞ Paris(0) 1 X X 785vLyon 1002vLyon Lyon(465) Chemin le plus court Paris → Lyon → Marseille de distance 785
Routage dans internet
Dans le contexte du routage Internet, les nœuds du graphe pourraient représenter des routeurs ou des commutateurs, et les arêtes pourraient représenter les connexions physiques ou virtuelles entre eux. Les poids sur les arêtes pourraient représenter des mesures de latence, de bande passante, ou d'autres métriques de performance de réseau.
# Création du graphe avec les sommets
noms_sommets = ['Routeur1', 'Routeur2', 'Routeur3', 'Routeur4', 'Routeur5',
'Ordinateur1', 'Ordinateur2', 'Serveur1', 'Serveur2', 'DNS1', 'DNS2']
matrice_adjacence = [[0, 2, 3, 0, 0, 1, 0, 0, 0, 0, 0], # Routeur1
[2, 0, 1, 2, 0, 0, 0, 1, 0, 0, 0], # Routeur2
[3, 1, 0, 4, 5, 0, 0, 0, 0, 5, 0], # Routeur3
[0, 2, 4, 0, 3, 0, 0, 0, 2, 0, 0], # Routeur4
[0, 0, 5, 3, 0, 0, 3, 0, 0, 0, 2], # Routeur5
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], # Ordinateur1
[0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0], # Ordinateur2
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], # Serveur1
[0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0], # Serveur2
[0, 0, 5, 0, 0, 0, 0, 0, 0, 0, 0], # DNS1
[0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0]] # DNS2
graphe = GrapheOrienteAvecPoids(noms_sommets)
# Ajout des arêtes directement
for i, sommetA in enumerate(noms_sommets):
for j, sommetB in enumerate(noms_sommets):
poids = matrice_adjacence[i][j]
if poids > 0: # Ajouter une arête uniquement si le poids est non nul
graphe.ajoute_arete(sommetA, sommetB, poids)
graphe.ajoute_arete(sommetB, sommetA, poids)
# Dessin du graphe
graphe.dessiner(figsize=(8, 8))
# Utiliser l'algorithme de Dijkstra pour trouver le chemin le plus court de Routeur1 à Serveur2
tableau_dijkstra, chemin_info = graphe.dijkstra_tableau('Ordinateur1', 'Serveur2')
print(tableau_dijkstra)
print()
print("Chemin le plus court", format_chemin(chemin_info[0]), "de distance", chemin_info[1])
Routeur1 Routeur2 Routeur3 ... DNS1 DNS2 Choix 0 1vOrdinateur1 ∞ ∞ ... ∞ ∞ Ordinateur1(0) 1 X 3vRouteur1 4vRouteur1 ... ∞ ∞ Routeur1(1) 2 X X 4vRouteur1 ... ∞ ∞ Routeur2(3) 3 X X X ... 9vRouteur3 ∞ Routeur3(4) 4 X X X ... 9vRouteur3 ∞ Serveur1(4) 5 X X X ... 9vRouteur3 ∞ Routeur4(5) [6 rows x 12 columns] Chemin le plus court Ordinateur1 → Routeur1 → Routeur2 → Routeur4 → Serveur2 de distance 7
Sujet BAC : Sujet 0A 24-NSIZERO-A Exercice n°3 + Correction

5.2 - Diviser pour régner ✔
Algorithmique
Méthode « diviser pour régner ».
Capacités attendues :
Écrire un algorithme utilisant la méthode « diviser pour régner ».
Commentaires :
La rotation d’une image bitmap d’un quart de tour avec un coût en mémoire constant est un bon exemple.
L’exemple du tri fusion permet également d’exploiter la récursivité et d’exhiber un algorithme de coût en $n log_2 n$
dans les pires des cas.

La méthode "diviser pour régner" est une technique algorithmique récursive qui permet de résoudre des problèmes complexes en les divisant en sous-problèmes plus simples, que l'on résout ensuite pour assembler la solution finale. Principe de base :
- Diviser : Le problème initial est divisé en plusieurs sous-problèmes plus petits.
- Régner : Chaque sous-problème est résolu indépendamment.
- Combiner : Les solutions des sous-problèmes sont combinées pour former la solution du problème initial.
Exemple 1: Tri Fusion (Merge Sort)
Le tri fusion est un bon exemple pour comprendre la méthode "diviser pour régner". Le problème de trier une liste peut être divisé en deux sous-problèmes de trier deux listes plus petites. Ensuite, on fusionne ces listes triées pour obtenir une liste triée complète.

Pseudo-code :
MergeSort(liste)
Si la longueur de la liste <= 1
Retourner liste
Sinon
Diviser la liste en deux moitiés : gauche, droite
gauche_triee = MergeSort(gauche)
droite_triee = MergeSort(droite)
Retourner Merge(gauche_triee, droite_triee)
Merge(gauche, droite)
resultat = []
Tant que gauche et droite sont non vides
Si premier élément de gauche < premier élément de droite
Ajouter premier élément de gauche à resultat
Supprimer premier élément de gauche
Sinon
Ajouter premier élément de droite à resultat
Supprimer premier élément de droite
Ajouter tous les éléments restants de gauche et droite à resultat
Retourner resultatdef merge_sort(arr):
# Cas de base: si la liste contient 0 ou 1 élément, elle est déjà triée.
if len(arr) <= 1:
return arr
# Divise la liste en deux moitiés
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
# Trie récursivement chaque moitié
sorted_left = merge_sort(left_half)
sorted_right = merge_sort(right_half)
# Fusionne les deux moitiés triées
return merge(sorted_left, sorted_right)
def merge(left, right):
result = []
i = j = 0
# Compare chaque élément des deux listes et ajoute le plus petit à 'result'
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
# Ajoute les éléments restants des deux listes (l'un des deux sera vide)
while i < len(left):
result.append(left[i])
i += 1
while j < len(right):
result.append(right[j])
j += 1
return result
# Test de la fonction
if __name__ == "__main__":
arr = [4, 3, 8, 2, 7, 1, 5]
sorted_arr = merge_sort(arr)
print("Tableau trié :", sorted_arr)Coût en temps de l'algorithme de tri fusion :
Propriété :
Pour trier une liste de taille n, le coût en temps de l'algorithme de tri fusion est O(n log2 n).
Démonstration :
Soit $N(n)$ le nombre d'opération mis par l'algorithme Tri Fusion (Merge Sort) pour trier une liste de longueur $n \geq 2$.
la divison des listes n'a pas de coût ?
Remontons l'arbre ci-dessus :
- Le niveau 0 de l'algorithme a besoin de $n$ opérations pour la fusion, car il faut déplacer $n$ nombres.
- Le niveau 1 a 2 sous-problèmes, chacun de taille $\frac{n}{2}$, donc l'algorithme a besoin de $n$ opérations pour la fusion, car il faut déplacer $n$ nombres.
- Le niveau 2 a 4 sous-problèmes, chacun de taille $\frac{n}{4}$, l'algorithme a besoin de $n$ opérations pour la fusion, car il faut déplacer $n$ nombres.
Et ainsi de suite... - le dernier niveau $k$ a 2$k$ sous-problèmes, chacun de taille $\frac{n}{2^k}$, l'algorithme a besoin de $n$ opérations pour la fusion, car il faut déplacer $n$ nombres.
k est le plus petit entier tel que $\frac{n}{2^k}\leq1$
$\frac{n}{2^k}\leq1 <=> n \leq 2^k <=> 2^k \geq n <=> k \geq log_2 n$
donc $ k \leq log_2 n + 1$
L'algorithme a besoin de $n$ opérations pour la fusion par niveau,
donc l'algorithme a besoin de $𝑛k$ opérations pour la fusion : $nk \leq n(log_2 n + 1)$
Pour la division des listes et des sous-listes, il y a aussi k niveau, autant de niveau que pour le fusion. Et pour diviser une $p$ listes de taille totale $n$, il faut déplacer $n$ nombres donc il faut n opérations par niveau. donc la aussi $nk$ opérations pour les division des sous-listes.
donc $N(n) = nk + nk \leq 2n(log_2 n + 1)$
donc $N(n) \leq 2n(log_2 n + log_2 n$) car $2 \leq n => 1 \leq log_2 n$
donc $N(n) \leq 4nlog_2 n$
Et donc le coût en terme de temps pour l'algorithme est $O(nlog_2 n)$. CQFD
Rotation d'une image avec un coût en mémoire constant en utilisant "diviser pour régner".
La méthode est illustrée sur le schéma ci-dessous :

- on coupe l'image en quatre quadrants ;
- on effectue une rotation récursive de chacun des quadrants ;
Nous utiliserons le module PIL.
L'image est à l'adresse : https://webftts.com/index_fichiers/Monstre.jpg
La taille de l'image est égale à une puissance de 2.

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
def rotate_quarter_turn(image):
n = image.shape[0]
# rotation de 1 pixel inutile
if n == 1:
return image
#création d'une image de même taille
new_image = np.zeros_like(image)
# division en 4 quadrants
half = n // 2
A = image[:half, :half]
B = image[:half, half:]
C = image[half:, :half]
D = image[half:, half:]
# Permutation des quadrants
new_image[:half, :half] = rotate_quarter_turn(B)
new_image[:half, half:] = rotate_quarter_turn(D)
new_image[half:, :half] = rotate_quarter_turn(A)
new_image[half:, half:] = rotate_quarter_turn(C)
return new_image
image = np.array(Image.open('Monstre.jpg'))
rotated_image = rotate_quarter_turn(image)
plt.imshow(rotated_image)
plt.title("Image après rotation récursive de 90 degrés")
plt.show()La rotation d'une image bitmap d'un quart de tour avec un coût en mémoire constant peut être réalisée en O(n2) pour une image de n x n pixels
Démonstration :
Soit $N(n)$ le nombre d'opération mis par l'algorithme Trotation pour une image de côté $n$.
- L'image est divisée en 4 quadrants égaux.
- Chaque quadrant subit ensuite une rotation récursive jusqu'à ce que la taille du quadrant soit 1 pixel, auquel cas la récursion se termine.
À chaque étape de la récursion, l'image est divisée en 4 parties plus petites, et la fonction de rotation est appelée 4 fois, une fois pour chaque quadrant.
Si $n$ est la longueur d'un côté de l'image (en supposant une image carrée), la profondeur de la récursion est $k$ tel que : $\frac{n}{2^k}\leq1 <=> n \leq 2^k <=> 2^k \geq n <=> k \geq log_2 n$ donc $ k \leq log_2 n + 1$
A chaque niveau de récursion, il y a 4 fois plus d'appels récursifs qu'au niveau précédent.
Ainsi, le nombre total d'appels récursifs est au maximum : $4^{log_2 n + 1}$
$4^{\log_2(n) + 1} = 4^{\log_2(n)} \times 4^1 = (2^2)^{\log_2(n)} \times 2^2 = 2^{2\log_2(n)} \times 2^2 = n^2 \times 4$
donc le nombre d'appels récurssif est $n^2 \times 4$.
Le coût des opérations dans chaque appel récursif de votre fonction de rotation d'image est constant car bien que la taille de l'image réduise de moitié dans chaque dimension à chaque appel récursif, les opérations effectuées restent les mêmes (diviser en quadrants, échanger les quadrants). Le fait que la taille de l'image soit plus petite ne change pas le nombre d'opérations élémentaires (comme les affectations ou les accès aux indices) qui doivent être effectuées.
Donc comme le coût des opérations dans chaque appel récursif est constant et égal à $c$, alors le nombre total d'opérations est $c \times $nombre d’appels recursifs, c'est-à-dire $c \times n^2 \times 4$.
donc $N(n) = c \times n^2 \times 4 = O(n^2)$
Considérations Pratiques :
Pour les très grandes images, cette méthode pourrait être inefficace en termes d'utilisation de la mémoire et de temps d'exécution, principalement en raison du grand nombre d'appels récursifs.
5.3 - Programmation dynamique
Algorithmique
Programmation dynamique
Capacités attendues :
Utiliser la programmation dynamique pour écrire un algorithme.
Commentaires :
- Les exemples de l’alignement de séquences ou du rendu de monnaie peuvent être présentés.
- La discussion sur le coût en mémoire peut être développée.
1. Principes Fondamentaux
La programmation dynamique est une méthode algorithmique utilisée pour résoudre des problèmes en décomposant ces derniers en sous-problèmes plus simples. Elle est couramment employée pour résoudre des problèmes d'optimisation, où l'objectif est de trouver la meilleure solution parmi un ensemble de solutions possibles.
La programmation dynamique repose sur deux principes fondamentaux :
-
Décomposition en Sous-Problèmes : Pour résoudre un problème complexe, la programmation dynamique le divise en une série de sous-problèmes plus petits et plus simples. Ces sous-problèmes doivent être indépendants les uns des autres, ce qui signifie que la solution à chaque sous-problème ne dépend que de la solution de sous-problèmes encore plus petits.
-
Stockage des Résultats Intermédiaires : Plutôt que de recalculer plusieurs fois la même solution pour un sous-problème donné, la programmation dynamique stocke les résultats intermédiaires dans une structure de données (généralement un tableau) pour éviter de recalculer les mêmes valeurs.
2. Exemple : Suite de Fibonacci
Revenons sur ce qui a été vu dans le cours consacré à la récursivité. On vous demandait d'écrire une fonction récursive qui permet de calculer le n ième terme de la suite de Fibonacci. Voici normalement ce que vous aviez dû obtenir :
from tutor import tutor
def Fibonacci1(n) :
if n < 2 :
return n
else :
return Fibonacci1(n-1)+Fibonacci1(n-2)
Fibonacci1(5)
tutor()Pour n=6, il est possible d'illustrer le fonctionnement de ce programme avec le schéma ci-dessous :
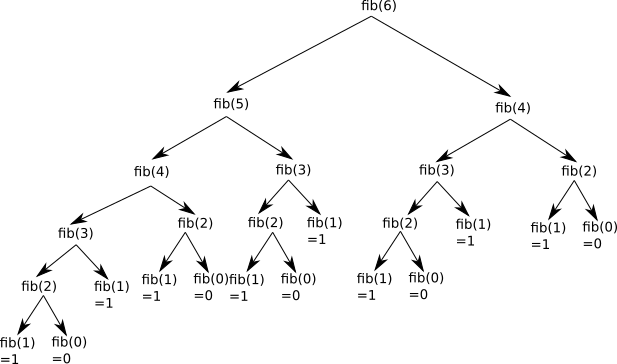
En observant attentivement le schéma ci-dessus, vous avez remarqué que de nombreux calculs sont inutiles, car effectué 2 fois :
On pourrait donc grandement simplifier le calcul en "mémorisant" le résultat et en le réutilisant quand nécessaire :
from tutor import tutor
def Fibonacci2(n):
if n < 2:
return n
else:
fib = [0] * (n + 1)
fib[1] = 1
for i in range(2, n + 1):
fib[i] = fib[i - 1] + fib[i - 2]
return fib[n]
Fibonacci2(6)
tutor()Complexité temporelle
-
La complexité de Fibonacci1 est de $O(2$$n$$)$, car chaque appel de la fonction génère deux autres appels, sauf pour les cas de base ($n < 2$). Cela conduit à un arbre d'appels où chaque niveau a deux fois plus d'appels que le niveau précédent. Le nombre total d'appels ressemble à un arbre binaire complet.
-
La complexité de Fibonacci2 est de $O(n)$, car cette méthode calcule chaque terme de la suite de Fibonacci une seule fois et les stocke dans un tableau. Chaque terme est calculé en temps constant à partir des deux termes précédents, donc la complexité est linéaire.
Complexité spatiale
Le coût en mémoire, aussi connu sous le terme de complexité spatiale, fait référence à la quantité de mémoire utilisée par un algorithme ou un programme informatique pendant son exécution. Ce coût est généralement mesuré en termes de la quantité de mémoire requise par rapport à la taille des données d'entrée.
Bien que la nature de l'utilisation de la mémoire est différente, la programmation dynamique utilise un espace mémoire pour le stockage de données (le tableau), tandis que la méthode récursive utilise la pile d'appels, les deux méthodes ont une complexité spatiale théorique de $O(n)$;
3. Problème du rendu de monaie
Le problème du rendu de monaie consiste à trouver le nombre minimal de pièces nécessaires pour rendre une somme donnée, en utilisant un ensemble prédéfini de valeurs de pièces.
Supposons que nous ayons des pièces de 1, 2, et 5 euros.
Le but est de rendre la somme de 11 euros en utilisant le moins de pièces possible.
def rendu_monaie_recursive(somme, pieces):
if somme == 0:
return 0
min_pieces = float('inf')
for piece in pieces:
if somme >= piece:
num_pieces = rendu_monaie_recursive(somme - piece, pieces)
if num_pieces != float('inf') and num_pieces + 1 < min_pieces:
min_pieces = num_pieces + 1
return min_pieces
pieces = [1, 2, 5]
somme = 11
result = rendu_monaie_recursive(somme, pieces)
print(f"Nombre minimal de pièces nécessaires pour rendre {somme} euros : {result}")Nombre minimal de pièces nécessaires pour rendre 11 euros : 3
def rendu_monaie_dynamique(somme,pieces):
tableau = [float('inf')] * (somme + 1)
tableau[0] = 0
for i in range(1, somme + 1):
for piece in pieces:
if i >= piece:
tableau[i] = min(tableau[i], tableau[i - piece] + 1)
return tableau[somme]
pieces = [1, 2, 5]
somme = 11
result = rendu_monaie_dynamique(somme, pieces)
print(f"Nombre minimal de pièces nécessaires pour rendre {somme} euros : {result}")Nombre minimal de pièces nécessaires pour rendre 11 euros : 3
Complexité temporelle
-
Dans la version récursive sans mémorisation, pour une somme $n$ et $m$ types de pièces, la complexité peut être très élevée. Chaque somme $s$ jusqu'à $n$ peut potentiellement être calculée $m$ fois, une fois pour chaque type de pièce qui peut être retiré de $s$. En d'autres termes, le nombre de façons de rendre la monnaie pour une somme $n$ peut être pensé comme un arbre de récursion où chaque nœud a $m$ enfants.
n / | \ n-a n-b n-c /|\ /|\ /|\ ... ... ... avec 3 types de pièces : a, b, et c
Cependant, cette estimation est assez grossière. En réalité, la complexité dépendra de la façon dont les valeurs de pièces disponibles se combinent pour former la somme cible. Dans le pire des cas, cela peut être de l'ordre $O(m^n)$.
- Dans le cas de la programmation dynamique, le nombre de calculs est beaucoup plus facile à déterminer. Pour une somme $n$ à rendre et $m$ types de pièces différentes, nous remplissons un tableau de taille $n+1$. Pour chaque entrée dans ce tableau, nous devons examiner $m$ types de pièces pour trouver le nombre minimum de pièces qui peuvent être utilisées pour rendre cette somme. Donc, le nombre total de calculs est $O((n+1)×m)$.
Complexité spatiale
Pour la programmation dynamique,pour une somme $n$, le nombre de mémoire est la taille du tableau $n+1$. Pour la programmation reccursive, le nombre d'appel recursif est au pire $n$. Doncune un pile de taille $n$. Donc là encore, les deux méthodes ont une complexité spatiale théorique de $O(n)$.
Mais, il est important de noter que, dans la pratique, l'approche récursive peut conduire à une très grande quantité d'appels récursifs pour de grandes sommes, ce qui peut entraîner un dépassement de pile (stack overflow) en raison de la limite de taille de la pile d'appels.
4. Alignement de séquences
La programmation dynamique est également fréquemment utilisée dans les problèmes d'alignement de séquences, comme l'alignement de séquences d'ADN ou de protéines. Un algorithme célèbre pour cela est l'algorithme de Needleman-Wunsch pour l'alignement de séquences globales ou l'algorithme de Smith-Waterman pour l'alignement de séquences locales.
4.1 Algorithme de Needleman-Wunsch (Alignement global)
Le concept d'alignement global est comme un jeu de puzzle où vous avez deux chaînes de caractères et vous essayez de les faire "correspondre" du mieux possible.
Pour faire cet alignement, nous utilisons des algorithmes qui calculent le "meilleur" alignement possible en fonction d'un "score". Ce score est calculé en fonction des règles que vous définissez. Par exemple, vous pourriez dire :
+1 point si les lettres sont identiques (match).
-1 point si les lettres sont différentes (mismatch).
-1 point si vous devez insérer un "trou" ou "gap" (représenté par un tiret '-') pour faire correspondre les lettres.L'algorithme examine toutes les possibilités et trouve l'alignement qui donne le score le plus élevé.
Lors du remplissage de la matrice d'alignement, l'une des trois actions possibles :
- Diagonal Move: Vous alignez deux caractères de vos deux séquences. Ce mouvement correspond à un "match" si les deux caractères sont identiques, ou à un "mismatch" s'ils sont différents.
- Vertical Move: Vous insérez un "gap" (espace) dans la première séquence pour l'aligner avec un caractère de la deuxième séquence. Ce mouvement correspond souvent à une pénalité dans le score de l'alignement.
- Horizontal Move: Vous insérez un "gap" dans la deuxième séquence pour l'aligner avec un caractère de la première séquence. Comme pour le mouvement vertical, ce mouvement entraîne généralement une pénalité dans le score de l'alignement.
Le Move choisie et celui qui donne le meilleur score.
def needleman_wunsch_with_traceback(seq1, seq2, match=1, mismatch=-1, gap=-1):
n, m = len(seq1), len(seq2)
dp = [[0] * (m + 1) for _ in range(n + 1)]
traceback = [[None] * (m + 1) for _ in range(n + 1)]
for i in range(n + 1):
dp[i][0] = i * gap
for j in range(m + 1):
dp[0][j] = j * gap
for i in range(1, n + 1):
for j in range(1, m + 1):
match_score = match if seq1[i - 1] == seq2[j - 1] else mismatch
choices = [dp[i-1][j-1] + match_score, dp[i-1][j] + gap, dp[i][j-1] + gap]
dp[i][j] = max(choices)
traceback[i][j] = choices.index(dp[i][j])
align1, align2 = "", ""
i, j = n, m
while i > 0 or j > 0:
if traceback[i][j] == 0: # Diagonal move
align1 = seq1[i - 1] + align1
align2 = seq2[j - 1] + align2
i -= 1
j -= 1
elif traceback[i][j] == 1: # Vertical move
align1 = seq1[i - 1] + align1
align2 = '-' + align2
i -= 1
else: # Horizontal move
align1 = '-' + align1
align2 = seq2[j - 1] + align2
j -= 1
return align1, align2, dp[-1][-1]
# Test
align1, align2, score = needleman_wunsch_with_traceback("GATTACA", "GCATGCU", match=1, mismatch=-1, gap=-1)
print("Score:", score)
print(align1)
print(align2)Score: 0 G-ATTACA GCA-TGCU
4.2 Algorithme de Smith-Waterman (Alignement local)
L'alignement local est une autre variante de l'alignement de séquences, mais contrairement à l'alignement global, il cherche à identifier les régions de séquences qui sont les plus similaires, même si ces régions sont de petite taille.Dans un alignement local, le calcul du score se focalise uniquement sur les segments les plus similaires des deux séquences, plutôt que d'essayer d'aligner les séquences dans leur intégralité. En d'autres termes, le but est de trouver la meilleure correspondance possible entre certaines parties des séquences, sans se soucier du reste.
def smith_waterman_with_traceback(seq1, seq2, match=1, mismatch=-1, gap=-1):
n, m = len(seq1), len(seq2)
dp = [[0] * (m + 1) for _ in range(n + 1)]
traceback = [[None] * (m + 1) for _ in range(n + 1)]
max_score = 0
max_i, max_j = 0, 0
for i in range(1, n + 1):
for j in range(1, m + 1):
match_score = match if seq1[i - 1] == seq2[j - 1] else mismatch
choices = [0, dp[i-1][j-1] + match_score, dp[i-1][j] + gap, dp[i][j-1] + gap]
dp[i][j] = max(choices)
traceback[i][j] = choices.index(dp[i][j])
if dp[i][j] >= max_score:
max_score = dp[i][j]
max_i, max_j = i, j
align1, align2 = "", ""
i, j = max_i, max_j
while dp[i][j] != 0:
if traceback[i][j] == 1: # Diagonal move
align1 = seq1[i - 1] + align1
align2 = seq2[j - 1] + align2
i -= 1
j -= 1
elif traceback[i][j] == 2: # Vertical move
align1 = seq1[i - 1] + align1
align2 = '-' + align2
i -= 1
else: # Horizontal move
align1 = '-' + align1
align2 = seq2[j - 1] + align2
j -= 1
return align1, align2, max_score
# Test
align1, align2, score = smith_waterman_with_traceback("GATTACA", "GCATGCU", match=1, mismatch=-1, gap=-1)
print("Score:", score)
print(align1)
print(align2)
Score: 2 CA CA
Complexité temporelle
Pour les algorithmes d'alignement de Needleman-Wunsch (alignement global) et Smith-Waterman (alignement local), la complexité est $O(n×m)$ où $n$ et $m$ sont les longueurs des deux séquences à aligner. Car, on doit approximativement $n×m$ calculs pour remplir la matrice d'alignement. Chaque cellule de cette matrice $n×m$ nécessite un calcul pour déterminer son score optimal en fonction des cellules adjacentes. Donc si vous avez deux séquences de longueurs $n$ et $m$ le nombre total de calculs sera proportionnel au produit de ces deux longueurs, soit $n×m$.
Complexité Spatiale :
Pour les algorithmes d'alignement de Needleman-Wunsch (alignement global) et Smith-Waterman (alignement local), la complexité spatiale est le nombre total de cellules dans la matrice, qui est $(n+1)× (m+1)$. Donc la complexité spatiale est aussi $O(n × m)$.
source : Pixees

5.4 - Recherche textuelle
Algorithmique
Recherche textuelle
Capacités attendues :
Étudier l’algorithme de Boyer-Moore pour la recherche d’un motif dans un texte.
Commentaires :
- L’intérêt du prétraitement du motif est mis en avant.
- L’étude du coût, difficile, ne peut être exigée
1. Recherche simple

def recherche_simple(texte, motif):
indices = []
i = 0
while i <= len(texte) - len(motif):
k = 0
while k < len(motif) and texte[i+k] == motif[k]:
k = k + 1
if k == len(motif):
indices.append(i)
i = i + 1
return indices
texte = "UNE MAGNIFIQUE MAISON BLEUE, UNE MAISON AVEC UN TOIT ROUGE."
motif = "MAISON"
print("Le motif a été trouvé aux positions :", recherche_simple(texte,motif))Le motif a été trouvé aux positions : [15, 33]
2. Algorithme de Boyer-Moore
 L'idée est d'améliorer le code précédent en sautant directement au prochain endroit potentiellement valide.
L'idée est d'améliorer le code précédent en sautant directement au prochain endroit potentiellement valide.Explication du fonctionnement de l'algorithme
-
Initialisation de la table de décalage :
lm = len(motif) : Calcule la longueur du motif à rechercher.
table = {} : Création d'un dictionnaire pour stocker le dernier indice de chaque caractère dans le motif, à l'exception du dernier caractère. -
Construction de la table de décalage :
La boucle for i in range(lm - 1): parcourt le motif de gauche à droite, à l'exception du dernier caractère.
Pour chaque caractère, table[motif[i]] = i stocke son indice dans la table. Si un caractère se répète, son indice le plus à droite est conservé. -
Recherche du motif dans le texte :
positions = []: Initialise une liste pour stocker les positions de départ de toutes les occurrences du motif dans le texte.
i = lm - 1: Commence la recherche à partir de l'indice dans le texte correspondant à la fin du motif. -
Boucle de recherche :
Tant que i < len(texte), on continue à chercher dans le texte.
k = 0: Initialise le compteur de correspondances.
La boucle interne while compare les caractères du motif avec ceux du texte de droite à gauche.
Si les caractères correspondent, k est incrémenté.- Si k == lm, tous les caractères du motif correspondent, et la position de début de l'occurrence est ajoutée à positions.
- Si le caractère actuel est dans la table, le décalage est calculé en prenant la différence entre la position du caractère dans le motif et sa position dans la table (i = i + lm - 1 - table[texte[i]]).
- Si le caractère n'est pas dans la table, le décalage est la longeur du motif entier (i = i + lm).
- Si k == lm, tous les caractères du motif correspondent, et la position de début de l'occurrence est ajoutée à positions.
-
Retour des positions :
La fonction retourne la liste des positions où le motif a été trouvé dans le texte.
def recherche_boyer_moore(texte, motif):
lm = len(motif)
table = {}
for p in range(lm - 1):
table[motif[p]] = p
positions = []
i = lm - 1
while i < len(texte):
k = 0
while k < lm and motif[lm - 1 - k] == texte[i - k]:
k = k + 1
if k == lm:
positions.append(i - lm + 1)
if texte[i] in table:
i = i + lm - 1 - table[texte[i]]
else:
i = i + lm
return positions
texte = "UNE MAGNIFIQUE MAISON BLEUE, UNE MAISON AVEC UN TOIT ROUGE."
motif = "MAISON"
print("Le motif a été trouvé aux positions :", recherche_boyer_moore(texte, motif))
texte = "MAMAMAMAMAMAMAMAMAMAMAMAMA"
motif = "MAMA"
print("Le motif a été trouvé aux positions :", recherche_boyer_moore(texte, motif))Le motif a été trouvé aux positions : [15, 33] Le motif a été trouvé aux positions : [0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22]
Remarque :
Plus le motif recherché est long, plus la recherche est rapide.
Le Projet Gutenberg permet de télécharger légalement des ouvrages libres de droits dans différents formats.
Vérifions notre remarque, avec le Tome 1 du roman Les Misérables de Victor Hugo, à télécharger ici ici au format txt, puis à importer dans basthon.
# Ouvre le fichier en mode de lecture ('r')
with open('Les_Miserables.txt', 'r') as fichier:
# Lit le contenu du fichier et le stocke dans la variable 'contenu'
texte = fichier.read()
print(texte[0:1000])Chapitre I Monsieur Myriel En 1815, M. Charles-François-Bienvenu Myriel était évêque de Digne. C'était un vieillard d'environ soixante-quinze ans; il occupait le siège de Digne depuis 1806. Quoique ce détail ne touche en aucune manière au fond même de ce que nous avons à raconter, il n'est peut-être pas inutile, ne fût-ce que pour être exact en tout, d'indiquer ici les bruits et les propos qui avaient couru sur son compte au moment où il était arrivé dans le diocèse. Vrai ou faux, ce qu'on dit des hommes tient souvent autant de place dans leur vie et surtout dans leur destinée que ce qu'ils font. M. Myriel était fils d'un conseiller au parlement d'Aix; noblesse de robe. On contait de lui que son père, le réservant pour hériter de sa charge, l'avait marié de fort bonne heure, à dix-huit ou vingt ans, suivant un usage assez répandu dans les familles parlementaires. Charles Myriel, nonobstant ce mariage, avait, disait-on, beaucoup fait parler de lui. Il était bien fait de sa personne
import time
def recherche_time(texte, motif):
début = time.time()
indices = recherche_simple(texte,motif)
fin = time.time()
print('indices :',indices)
print('temps :',fin-début)
print()
recherche_time(texte,"Jean Valjean avait laissé, le plus d'argent possible aux pauvres")
recherche_time(texte,"maison")indices : [654457] temps : 2.065999984741211 indices : [7264, 9090, 9547, 9745, 10936, 17820, 23978, 38192, 41639, 41651, 41840, 42493, 48028, 48393, 51448, 53353, 70867, 72692, 72768, 75608, 77855, 108489, 115739, 130629, 132983, 138870, 143681, 144600, 153114, 155973, 158709, 160700, 163649, 169164, 169181, 171761, 171967, 182642, 186413, 190534, 219378, 220314, 224518, 225098, 227579, 296302, 345108, 345893, 346740, 349677, 359727, 362025, 389945, 395690, 434118, 438068, 457795, 457886, 464696, 469403, 501768, 514980, 520667, 520878, 520926, 520968, 522707, 529329, 598128, 601390, 645915] temps : 2.116000175476074
import time
def recherche_time(texte, motif):
début = time.time()
indices = recherche_boyer_moore(texte,motif)
fin = time.time()
print('indices :',indices)
print('temps :',fin-début)
print()
recherche_time(texte,"Jean Valjean avait laissé, le plus d'argent possible aux pauvres")
recherche_time(texte,"maison")indices : [654457] temps : 0.03899979591369629 indices : [7264, 9090, 9547, 9745, 10936, 17820, 23978, 38192, 41639, 41651, 41840, 42493, 48028, 48393, 51448, 53353, 70867, 72692, 72768, 75608, 77855, 108489, 115739, 130629, 132983, 138870, 143681, 144600, 153114, 155973, 158709, 160700, 163649, 169164, 169181, 171761, 171967, 182642, 186413, 190534, 219378, 220314, 224518, 225098, 227579, 296302, 345108, 345893, 346740, 349677, 359727, 362025, 389945, 395690, 434118, 438068, 457795, 457886, 464696, 469403, 501768, 514980, 520667, 520878, 520926, 520968, 522707, 529329, 598128, 601390, 645915] temps : 0.1119999885559082
import os
repertoire = "."
fichiers = [f for f in os.listdir(repertoire) if os.path.isfile(os.path.join(repertoire, f))]
print(f"fichiers : {fichiers}")
for fichier in fichiers:
chemin_complet = os.path.join(repertoire, fichier)
os.remove(chemin_complet)
print(f"Le fichier {fichier} a été supprimé.")fichiers : ['Les_Miserables.txt'] Le fichier Les_Miserables.txt a été supprimé.
source : glassus

01 - Hanoï ✔
La tour de Brahma
Dans ses récits de voyages, $B.$ $Rynhe$ $de$ $Tioch$ dit avoir vu, un temple où les moines veillent sur 64 disques sacrés en or.
Tous de tailles différentes, ils sont enfilés sur trois aiguilles de diamant. Au commencement Brahma les confia sur la première aiguille au Mahābhārata avec la mission de les déplacer sur la troisième en respectant les 2 règles intangibles :
- Un disque ne peut reposer que sur un plus large.
- Les disques ne peuvent être manipulés qu’un à un d’une aiguille vers une autre.

Nuit et jour, les moines se succèdent sur les marches de l’autel, occupés à transporter la tour de la première aiguille vers la troisième sans s’écarter des règles.
Ils ont en permanence en tête la terrible prophétie : Quand tout sera fini, la tour et les brahmes tomberont, et ce sera la fin des mondes !
- Qu’en pensez ?
Il peut sembler impossible de trouver le nombre de déplacements que les moines effectueront.
Cependant,
- pour déplacer le plus grand disque sur une aiguille, il faut au minimum amener tous les disques au-dessus de lui (soit une tour avec un disque en moins) sur une aiguille intermédiaire, pour « libérer » ce plus grand disque.
- s'il n'y a qu'un disque, il suffit d'un déplacement (au minimum) pour l'amener en position finale.
Aussi étonnant que cela puisse paraitre, cela suffit pour programmer le calcul du nombre minimal de déplacements à effectuer pour un nombre donné de disques.
- Lisez attentivement l'algorithme ci-dessous :
L'algorithme "récursif" :
fonction nb_deplace(n):
"""cette fonction reçoit un nombre n de disques
et renvoie le nombre de déplacements nécessaires """
si n = 1 :
renvoyer 1 # 1 disque donc 1 déplacement
sinon :
d = nb_deplace(n-1) # Il y a n-1 disques à bouger pour "libérer" le plus grand.
renvoyer d + 1 + d
# d mouvements pour les n-1 disques au-dessus du grand disque
# 1 mouvement pour le disque libéré
# d mouvements pour amener les n-1 disques sur le plus grand Il s'agit d'une fonction qui s'appelle elle-même, c'est pour cela qu'on la qualifie de récursive.
Lorsque que $n$ est un entier strictement positif, l'algorithme se termine !
En effet,
- la fonction s'auto appelle au plus $n$ fois, puisque $n$ diminue de 1 à chaque appel.
- le dernier appel de la fonction est
nb_deplace(1)qui renvoie 1
Attention, un appel de la fonction avec un nombre négatif ou un nombre non entier génère une infinité d'appel de la fonction par elle-même et alors l'algorithme ne se termine jamais.
- Complétez la traduction de cet algorithme en python.
def nb_deplace(n):
if n == 1:
return …
else :
d = nb_deplace(…)
return d + 1 + dVérifions les premiers résultats :
On sait qu'une tour de 1 disque est déplacée en 1 mouvement.nb_deplace(1)- Complétez les pointillés ci-dessous jusqu'au calcul du temps nécessaire.
Selon l'algorithme,
nb_deplace(2)- Une tour de 2 disques est déplacée en … mouvements.
Prenez 2 pièces de monnaie différentes (ou 2 objets superposables), trouvez l'ordre dans lequel elles doivent être déplacées et complétez ce tableau. | mouvement | depuis l'aiguille | vers l'aiguille| |:---|:----:|:-----:| |1| … | … | |2| … | … | |3| … | … |
Selon l'algorithme,
nb_deplace(3)- Une tour de 3 disques est déplacée en … mouvements.
Prenez 3 pièces de monnaie différentes (ou 3 objets superposables), trouvez l'ordre dans lequel elles doivent être déplacées et complétez ce tableau. Ajoutez des lignes autant que nécessaire. | mouvement | depuis l'aiguille | vers l'aiguille| |:---|:----:|:-----:| |1| … | … | |2| … | … | |3| … | … | |4| … | … | |5| … | … | |6| … | … |
Comptez le nombre de déplacements sur cette animation pour 4 disques et vérifiez que la fonction donne le même nombre.

nb_deplace(4)- Une tour de 4 disques est déplacée en … mouvements.
Le nombre de déplacements indiqué par la fonction semble correct.
- Calculez le nombre de déplacement pour la tour de Brahma.
nb_deplace(…) # Brahma a confié 64 disques au Mahābhārata Le temps nécessaire
Comme le nombre de déplacements est grand, pour nous faire une idée, décidons qu'un disque est déplacé en une seconde.
- Écrivez ci-dessous le calcul donnant le nombre de disques déplacés en une année.
Voici quelques points de repère :
- L'homme a inventé l'écriture il y a 5 à 6 mille ans.
- L'homme serait apparu (en fait une très lente évolution de plusieurs centaines de milliers d'années) sur terre, il y a 3 millions d'années.
- L'âge de la terre est estimé à 4,5 milliards d'années.
- L'âge du système solaire est estimé à 4,6 milliards d'années.
- D'ici environ 5 milliards d'années le soleil aura considérablement grossi, il sera devenu une géante rouge et aura englouti la terre.
- un travail récent de l'Université de Cornell estime l'âge de l'univers à 13,7 milliards d'années.
- Que pensez-vous de la prophétie : « Quand tout sera fini, la tour et les brahmes tomberont, et ce sera la fin des mondes ! » ?
# vous pouvez faire des calculs iciCette situation a été créée dans des termes très proches par Edouard Lucas en 1889.
Merci à Bruno HENRY
Grand Oral
Python
# Résulution de Chatgpt pour la tour de Hanoï
def hanoi(n, source, target, auxiliary, towers):
if n == 1:
disk = towers[source].pop()
towers[target].append(disk)
draw_towers(towers)
return
hanoi(n-1, source, auxiliary, target, towers)
disk = towers[source].pop()
towers[target].append(disk)
draw_towers(towers)
hanoi(n-1, auxiliary, target, source, towers)
def draw_towers(towers):
for name, tower in towers.items():
print(f"{name}: {tower}")
print("-----")
def init_towers(n):
towers = {
'A': list(range(n, 0, -1)), # [n, n-1, ..., 2, 1]
'B': [],
'C': []
}
return towers
n = int(input("Enter the number of disks: ")) # Get the number of disks from the user
towers = init_towers(n)
draw_towers(towers) # Draw initial state
hanoi(n, 'A', 'C', 'B', towers)Enter the number of disks: 5 A: [5, 4, 3, 2, 1] B: [] C: [] ----- A: [5, 4, 3, 2] B: [] C: [1] ----- A: [5, 4, 3] B: [2] C: [1] ----- A: [5, 4, 3] B: [2, 1] C: [] ----- A: [5, 4] B: [2, 1] C: [3] ----- A: [5, 4, 1] B: [2] C: [3] ----- A: [5, 4, 1] B: [] C: [3, 2] ----- A: [5, 4] B: [] C: [3, 2, 1] ----- A: [5] B: [4] C: [3, 2, 1] ----- A: [5] B: [4, 1] C: [3, 2] ----- A: [5, 2] B: [4, 1] C: [3] ----- A: [5, 2, 1] B: [4] C: [3] ----- A: [5, 2, 1] B: [4, 3] C: [] ----- A: [5, 2] B: [4, 3] C: [1] ----- A: [5] B: [4, 3, 2] C: [1] ----- A: [5] B: [4, 3, 2, 1] C: [] ----- A: [] B: [4, 3, 2, 1] C: [5] ----- A: [1] B: [4, 3, 2] C: [5] ----- A: [1] B: [4, 3] C: [5, 2] ----- A: [] B: [4, 3] C: [5, 2, 1] ----- A: [3] B: [4] C: [5, 2, 1] ----- A: [3] B: [4, 1] C: [5, 2] ----- A: [3, 2] B: [4, 1] C: [5] ----- A: [3, 2, 1] B: [4] C: [5] ----- A: [3, 2, 1] B: [] C: [5, 4] ----- A: [3, 2] B: [] C: [5, 4, 1] ----- A: [3] B: [2] C: [5, 4, 1] ----- A: [3] B: [2, 1] C: [5, 4] ----- A: [] B: [2, 1] C: [5, 4, 3] ----- A: [1] B: [2] C: [5, 4, 3] ----- A: [1] B: [] C: [5, 4, 3, 2] ----- A: [] B: [] C: [5, 4, 3, 2, 1] -----
02 - Hanoï (Correction) ✔
La tour de Brahma - Correction
Dans ses récits de voyages, $B.$ $Rynhe$ $de$ $Tioch$ dit avoir vu, un temple où les moines veillent sur 64 disques sacrés en or.
Tous de tailles différentes, ils sont enfilés sur trois aiguilles de diamant. Au commencement Brahma les confia sur la première aiguille au Mahābhārata avec la mission de les déplacer sur la troisième en respectant les 2 règles intangibles :
- Un disque ne peut reposer que sur un plus large.
- Les disques ne peuvent être manipulés qu’un à un d’une aiguille vers une autre.

Nuit et jour, les moines se succèdent sur les marches de l’autel, occupés à transporter la tour de la première aiguille vers la troisième sans s’écarter des règles.
Ils ont en permanence en tête la terrible prophétie : Quand tout sera fini, la tour et les brahmes tomberont, et ce sera la fin des mondes !
- Qu’en pensez ?
Il peut sembler impossible de trouver le nombre de déplacements que les moines effectueront.
Cependant,
- pour déplacer le plus grand disque sur une aiguille, il faut au minimum amener tous les disques au-dessus de lui (soit une tour avec un disque en moins) sur une aiguille intermédiaire, pour « libérer » ce plus grand disque.
- s'il n'y a qu'un disque, il suffit d'un déplacement (au minimum) pour l'amener en position finale.
Aussi étonnant que cela puisse paraitre, cela suffit pour programmer le calcul du nombre minimal de déplacements à effectuer pour un nombre donné de disques.
- Lisez attentivement l'algorithme ci-dessous :
L'algorithme "récursif" :
fonction nb_deplace(n):
"""cette fonction reçoit un nombre n de disques
et renvoie le nombre de déplacements nécessaires """
si n = 1 :
renvoyer 1 # 1 disque donc 1 déplacement
sinon :
d = nb_deplace(n-1) # Il y a n-1 disques à bouger pour "libérer" le plus grand.
renvoyer d + 1 + d
# d mouvements pour les n-1 disques au-dessus du grand disque
# 1 mouvement pour le disque libéré
# d mouvements pour amener les n-1 disques sur le plus grand Il s'agit d'une fonction qui s'appelle elle-même, c'est pour cela qu'on la qualifie de récursive.
Lorsque que $n$ est un entier strictement positif, l'algorithme se termine !
En effet,
- la fonction s'auto appelle au plus $n$ fois, puisque $n$ diminue de 1 à chaque appel.
- le dernier appel de la fonction est
nb_deplace(1)qui renvoie 1
Attention, un appel de la fonction avec un nombre négatif ou un nombre non entier génère une infinité d'appel de la fonction par elle-même et alors l'algorithme ne se termine jamais.
- Complétez la traduction de cet algorithme en python.
def nb_deplace(n):
if n == 1:
return 1
else :
d = nb_deplace(n-1)
return d + 1 + dVérifions les premiers résultats :
On sait qu'une tour de 1 disque est déplacée en 1 mouvement.nb_deplace(1)- Complétez les pointillés ci-dessous jusqu'au calcul du temps nécessaire.
Selon l'algorithme,
nb_deplace(2)- Une tour de 2 disques est déplacée en 3 mouvements.
Prenez 2 pièces de monnaie différentes (ou 2 objets superposables), trouvez l'ordre dans lequel elles doivent être déplacées et complétez ce tableau. | mouvement | depuis l'aiguille | vers l'aiguille| |:---|:----:|:-----:| |1| 1 | 2 | |2| 1 | 3 | |3| 2 | 3 |
Selon l'algorithme,
nb_deplace(3)Une tour de 3 disques est déplacée en 7 mouvements.
Prenez 3 pièces de monnaie différentes (ou 3 objets superposables), trouvez l'ordre dans lequel elles doivent être déplacées et complétez ce tableau. Ajoutez des lignes autant que nécessaire. | mouvement | depuis l'aiguille | vers l'aiguille| |:---|:----:|:-----:| |1| 1 | 3 | |2| 1 | 2 | |3| 3 | 2 | |4| 1 | 3 | |5| 2 | 1 | |6| 2 | 3 | |7| 1 | 3 |
Comptez le nombre de déplacements sur cette animation pour 4 disques et vérifiez que la fonction donne le même nombre.

nb_deplace(4)- Une tour de 4 disques est déplacée en 15 mouvements.
Le nombre de déplacements indiqué par la fonction semble correct.
- Calculez le nombre de déplacement pour la tour de Brahma.
nb_deplace(64) # Brahma a confié 64 disques au Mahābhārata Le temps nécessaire
Comme le nombre de déplacements est grand, pour nous faire une idée, décidons qu'un disque est déplacé en une seconde.
- Écrivez ci-dessous le calcul donnant le nombre de disques déplacés en une année.
nb_deplace(64)/(60*60*24*365)Voici quelques points de repère :
- L'homme a inventé l'écriture il y a 5 à 6 mille ans.
- L'homme serait apparu (en fait une très lente évolution de plusieurs centaines de milliers d'années) sur terre, il y a 3 millions d'années.
- L'âge de la terre est estimé à 4,5 milliards d'années.
- L'âge du système solaire est estimé à 4,6 milliards d'années.
- D'ici environ 5 milliards d'années le soleil aura considérablement grossi, il sera devenu une géante rouge et aura englouti la terre.
- un travail récent de l'Université de Cornell estime l'âge de l'univers à 13,7 milliards d'années.
- Que pensez-vous de la prophétie : « Quand tout sera fini, la tour et les brahmes tomberont, et ce sera la fin des mondes ! » ?
print(nb_deplace(64)/(60*60*24*365*10**9), " milliards d'années")584.942417355072 milliards d'années
Cette situation a été créée dans des termes très proches par Edouard Lucas en 1889.
Merci à Bruno HENRY
Grand Oral
Python
# Résulution de Chatgpt pour la tour de Hanoï
def hanoi(n, source, target, auxiliary, towers):
if n == 1:
disk = towers[source].pop()
towers[target].append(disk)
draw_towers(towers)
return
hanoi(n-1, source, auxiliary, target, towers)
disk = towers[source].pop()
towers[target].append(disk)
draw_towers(towers)
hanoi(n-1, auxiliary, target, source, towers)
def draw_towers(towers):
for name, tower in towers.items():
print(f"{name}: {tower}")
print("-----")
def init_towers(n):
towers = {
'A': list(range(n, 0, -1)), # [n, n-1, ..., 2, 1]
'B': [],
'C': []
}
return towers
n = int(input("Enter the number of disks: ")) # Get the number of disks from the user
towers = init_towers(n)
draw_towers(towers) # Draw initial state
hanoi(n, 'A', 'C', 'B', towers)Enter the number of disks: 3 A: [3, 2, 1] B: [] C: [] ----- A: [3, 2] B: [] C: [1] ----- A: [3] B: [2] C: [1] ----- A: [3] B: [2, 1] C: [] ----- A: [] B: [2, 1] C: [3] ----- A: [1] B: [2] C: [3] ----- A: [1] B: [] C: [3, 2] ----- A: [] B: [] C: [3, 2, 1] -----
03 - Jeu 1 ✔
Tic Tac Toc - Puissance 4 - Tour de Hanoï
Tic Tac Toc vs Computer - Récursivité
Vidéo : WarGames 1983
# Évaluation des états du tableau
def evaluate(board):
for row in board:
if row[0] == row[1] == row[2]:
if row[0] == "X":
return 10
elif row[0] == "O":
return -10
for col in range(3):
if board[0][col] == board[1][col] == board[2][col]:
if board[0][col] == "X":
return 10
elif board[0][col] == "O":
return -10
if board[0][0] == board[1][1] == board[2][2]:
if board[0][0] == "X":
return 10
elif board[0][0] == "O":
return -10
if board[0][2] == board[1][1] == board[2][0]:
if board[0][2] == "X":
return 10
elif board[0][2] == "O":
return -10
return 0
# Fonction Minimax
def minimax(board, depth, maximizing):
score = evaluate(board)
if score == 10:
return score
if score == -10:
return score
if not any("_" in row for row in board):
return 0
if maximizing:
maxEval = float("-inf")
for i in range(3):
for j in range(3):
if board[i][j] == "_":
board[i][j] = "X"
eval = minimax(board, depth + 1, False)
board[i][j] = "_"
maxEval = max(maxEval, eval)
return maxEval
else:
minEval = float("inf")
for i in range(3):
for j in range(3):
if board[i][j] == "_":
board[i][j] = "O"
eval = minimax(board, depth + 1, True)
board[i][j] = "_"
minEval = min(minEval, eval)
return minEval
def findBestMove(board):
bestValue = float("-inf")
bestMove = (-1, -1)
for i in range(3):
for j in range(3):
if board[i][j] == "_":
board[i][j] = "X"
moveValue = minimax(board, 0, False)
board[i][j] = "_"
if moveValue > bestValue:
bestMove = (i, j)
bestValue = moveValue
return bestMove
# Fonction principale pour jouer à Tic-Tac-Toe
if __name__ == "__main__":
board = [
["_", "_", "_"],
["_", "_", "_"],
["_", "_", "_"]
]
pad_to_idx = {
"1": (0, 0), "2": (0, 1), "3": (0, 2),
"4": (1, 0), "5": (1, 1), "6": (1, 2),
"7": (2, 0), "8": (2, 1), "9": (2, 2)
}
for row in board:
print(" ".join(row))
print()
while True:
move = input("Enter your move (1-9 like the numeric pad) or q to quit: ")
if move.lower() == 'q':
print("Game terminated by user.")
break
if move in pad_to_idx:
x, y = pad_to_idx[move]
if board[x][y] not in ["X", "O"]:
board[x][y] = "O"
# Afficher le plateau après le coup de l'utilisateur
print("Your move:")
for row in board:
print(" ".join(row))
print()
if evaluate(board) == -10:
print("You win!")
break
bestMove = findBestMove(board)
board[bestMove[0]][bestMove[1]] = "X"
if evaluate(board) == 10:
print("Computer wins!")
for row in board:
print(" ".join(row))
print()
break
if not any("_" in row for row in board):
print("It's a draw!")
for row in board:
print(" ".join(row))
print()
break
# Afficher le plateau après le coup de l'ordinateur
print("Computer played:")
for row in board:
print(" ".join(row))
print()
else:
print("Invalid move. Try again.")
else:
print("Invalid number. Try again.")
_ _ _ _ _ _ _ _ _
Puissance 4 avec choix de la profondeur de récursivité
import copy
def print_board(board):
for row in board:
print(" ".join(row))
print("0 1 2 3 4 5 6\n")
print() # Ajout d'une ligne vide pour la clarté
def is_valid_move(board, col):
return board[0][col] == "-"
def make_move(board, col, player):
for i in reversed(range(len(board))):
if board[i][col] == "-":
board[i][col] = player
return True
return False
def is_winner(board, player):
for row in range(6):
for col in range(7):
if board[row][col] == player:
# Vérifiez à l'horizontale
if col <= 3 and all(board[row][c] == player for c in range(col, col + 4)):
return True
# Vérifiez à la verticale
if row <= 2 and all(board[r][col] == player for r in range(row, row + 4)):
return True
# Vérifiez la diagonale vers la droite
if row <= 2 and col <= 3 and all(board[row + r][col + c] == player for r, c in zip(range(4), range(4))):
return True
# Vérifiez la diagonale vers la gauche
if row <= 2 and col >= 3 and all(board[row + r][col - c] == player for r, c in zip(range(4), range(4))):
return True
return False
def minimax(board, depth, maximizing, alpha, beta):
if is_winner(board, "X"):
return -10
if is_winner(board, "O"):
return 10
if all(cell != "-" for row in board for cell in row) or depth == 0:
return 0
if maximizing:
max_eval = float('-inf')
for col in range(7):
if is_valid_move(board, col):
new_board = copy.deepcopy(board)
make_move(new_board, col, "O")
eval = minimax(new_board, depth-1, False, alpha, beta)
max_eval = max(max_eval, eval)
alpha = max(alpha, eval)
if beta <= alpha:
break
return max_eval
else:
min_eval = float('inf')
for col in range(7):
if is_valid_move(board, col):
new_board = copy.deepcopy(board)
make_move(new_board, col, "X")
eval = minimax(new_board, depth-1, True, alpha, beta)
min_eval = min(min_eval, eval)
beta = min(beta, eval)
if beta <= alpha:
break
return min_eval
if __name__ == "__main__":
board = [["-" for _ in range(7)] for _ in range(6)]
depth = int(input("Entrez la profondeur de recherche pour l'ordinateur: "))
while True:
print_board(board)
col = int(input("Votre coup (0-6): "))
if is_valid_move(board, col):
make_move(board, col, "X")
if is_winner(board, "X"):
print_board(board)
print("Vous avez gagné!")
break
best_val = float('-inf')
best_col = 0
for col in range(7):
if is_valid_move(board, col):
new_board = copy.deepcopy(board)
make_move(new_board, col, "O")
move_val = minimax(new_board, depth, False, float('-inf'), float('inf'))
if move_val > best_val:
best_col = col
best_val = move_val
make_move(board, best_col, "O")
if is_winner(board, "O"):
print_board(board)
print("L'ordinateur a gagné!")
break
Entrez la profondeur de recherche pour l'ordinateur: 5 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 0 1 2 3 4 5 6 Votre coup (0-6): 0 - - - - - - - - - - - - - - - - - - - - - - - - - - - - O - - - - - - X - - - - - - 0 1 2 3 4 5 6 Votre coup (0-6): 1 - - - - - - - - - - - - - - - - - - - - - O - - - - - - O - - - - - - X X - - - - - 0 1 2 3 4 5 6 Votre coup (0-6): 2 - - - - - - - - - - - - - - - - - - - - - O - - - - - - O - - - - - - X X X O - - - 0 1 2 3 4 5 6 Votre coup (0-6): 0 - - - - - - - O - - - - - - X - - - - - - O - - - - - - O - - - - - - X X X O - - - 0 1 2 3 4 5 6 Votre coup (0-6): 3 O - - - - - - O - - - - - - X - - - - - - O - - - - - - O - - X - - - X X X O - - - 0 1 2 3 4 5 6 Votre coup (0-6): 2 O - - - - - - O - - - - - - X - - - - - - O - - - - - - O O X X - - - X X X O - - - 0 1 2 3 4 5 6 Votre coup (0-6): 2 O - - - - - - O - - - - - - X - O - - - - O - X - - - - O O X X - - - X X X O - - - 0 1 2 3 4 5 6 Votre coup (0-6): 1 O - - - - - - O - - - - - - X O O - - - - O X X - - - - O O X X - - - X X X O - - - 0 1 2 3 4 5 6 Votre coup (0-6): 3 O - - - - - - O O - - - - - X O O - - - - O X X X - - - O O X X - - - X X X O - - - 0 1 2 3 4 5 6 Votre coup (0-6): 4 O O - - - - - O O - - - - - X O O - - - - O X X X - - - O O X X - - - X X X O X - - 0 1 2 3 4 5 6 Votre coup (0-6): 5 O O - - - - - O O O - - - - X O O - - - - O X X X - - - O O X X - - - X X X O X X - 0 1 2 3 4 5 6 Votre coup (0-6): 5 O O O - - - - O O O - - - - X O O - - - - O X X X - - - O O X X - X - X X X O X X - 0 1 2 3 4 5 6 Votre coup (0-6): 4 O O O - - - - O O O - - - - X O O - - - - O X X X - - - O O X X X X - X X X O X X - 0 1 2 3 4 5 6 Vous avez gagné!
Tour de Hanoï résolution récursive
def hanoi(n, source, target, auxiliary, towers):
if n == 1:
disk = towers[source].pop()
towers[target].append(disk)
draw_towers(towers)
return
hanoi(n-1, source, auxiliary, target, towers)
disk = towers[source].pop()
towers[target].append(disk)
draw_towers(towers)
hanoi(n-1, auxiliary, target, source, towers)
def draw_towers(towers):
for name, tower in towers.items():
print(f"{name}: {tower}")
print("-----")
def init_towers(n):
towers = {
'A': list(range(n, 0, -1)), # [n, n-1, ..., 2, 1]
'B': [],
'C': []
}
return towers
n = int(input("Enter the number of disks: ")) # Get the number of disks from the user
towers = init_towers(n)
draw_towers(towers) # Draw initial state
hanoi(n, 'A', 'C', 'B', towers)
Enter the number of disks: 5 A: [5, 4, 3, 2, 1] B: [] C: [] ----- A: [5, 4, 3, 2] B: [] C: [1] ----- A: [5, 4, 3] B: [2] C: [1] ----- A: [5, 4, 3] B: [2, 1] C: [] ----- A: [5, 4] B: [2, 1] C: [3] ----- A: [5, 4, 1] B: [2] C: [3] ----- A: [5, 4, 1] B: [] C: [3, 2] ----- A: [5, 4] B: [] C: [3, 2, 1] ----- A: [5] B: [4] C: [3, 2, 1] ----- A: [5] B: [4, 1] C: [3, 2] ----- A: [5, 2] B: [4, 1] C: [3] ----- A: [5, 2, 1] B: [4] C: [3] ----- A: [5, 2, 1] B: [4, 3] C: [] ----- A: [5, 2] B: [4, 3] C: [1] ----- A: [5] B: [4, 3, 2] C: [1] ----- A: [5] B: [4, 3, 2, 1] C: [] ----- A: [] B: [4, 3, 2, 1] C: [5] ----- A: [1] B: [4, 3, 2] C: [5] ----- A: [1] B: [4, 3] C: [5, 2] ----- A: [] B: [4, 3] C: [5, 2, 1] ----- A: [3] B: [4] C: [5, 2, 1] ----- A: [3] B: [4, 1] C: [5, 2] ----- A: [3, 2] B: [4, 1] C: [5] ----- A: [3, 2, 1] B: [4] C: [5] ----- A: [3, 2, 1] B: [] C: [5, 4] ----- A: [3, 2] B: [] C: [5, 4, 1] ----- A: [3] B: [2] C: [5, 4, 1] ----- A: [3] B: [2, 1] C: [5, 4] ----- A: [] B: [2, 1] C: [5, 4, 3] ----- A: [1] B: [2] C: [5, 4, 3] ----- A: [1] B: [] C: [5, 4, 3, 2] ----- A: [] B: [] C: [5, 4, 3, 2, 1] -----
03 - Jeu 2 ✔
Rudi's Cube 2x2 - Rudi's Cube 3x3
Site de résolution de nombreus de Rubi's cubes : https://rubiks-cube-solver.com/2x2/
Rudi's Cube 2x2 - récurcivité et force brute
# Temps en s Nd de coups essayés
# 1 0 13
# 2 0,01562 170
# 3 0,18502 2055
# 4 2,20833 24676
# 5 24,4204 296129
# 6 289,04738 3553566
# 7 3649,51091 42642811
# 8 41209,38342 511713752
# 9 494512,601 = 137 h (prévision)
#10 5934151,212
#11 71209814,55 = 2,25 ans (prévision) n=11 est la borne de Dieu !!!
# site de résolution : https://rubiks-cube-solver.com/2x2/
import numpy as np
import time
# U pour "Up", D pour "Down", L pour "Left", R pour "Right", F pour "Front", B pour "Back"
# 'w' pour blanc, 'g' pour vert, 'r' pour rouge, 'b' pour bleu, 'o' pour orange, 'y' pour jaune
# F: Rotation de la face avant dans le sens horaire.
# B: Rotation de la face arrière dans le sens horaire.
# R: Rotation de la face droite dans le sens horaire.
# L: Rotation de la face gauche dans le sens horaire.
# U: Rotation de la face supérieure dans le sens horaire.
# D: Rotation de la face inférieure dans le sens horaire.
def affichage(cube):
# La face U (Up)
for row in cube[0]:
print(" ", end="")
print(" ".join(row))
print()
# Les faces L (Left), F (Front), R (Right), B (Back)
for i in range(2):
for face in [2, 4, 3, 5]:
print(" ".join(cube[face][i]), end=" ")
print()
print()
# La face D (Down)
for row in cube[1]:
print(" ", end="")
print(" ".join(row))
print()
def F(cube):
cube[4] = np.rot90(cube[4], -1)
temp_U = np.copy(cube[0][1, :])
temp_R = np.copy(cube[3][:, 0])
temp_D = np.copy(cube[1][0, :])
temp_L = np.copy(cube[2][:, 1])
cube[0][1, :] = temp_L[::-1]
cube[3][:, 0] = temp_U
cube[1][0, :] = temp_R[::-1]
cube[2][:, 1] = temp_D
return cube
def F_inv(cube):
cube[4] = np.rot90(cube[4], 1)
temp_U = np.copy(cube[0][1, :])
temp_R = np.copy(cube[3][:, 0])
temp_D = np.copy(cube[1][0, :])
temp_L = np.copy(cube[2][:, 1])
cube[0][1, :] = temp_R
cube[3][:, 0] = temp_D[::-1]
cube[1][0, :] = temp_L
cube[2][:, 1] = temp_U[::-1]
return cube
def L(cube):
cube[2] = np.rot90(cube[2], -1)
temp_U = np.copy(cube[0][:, 0])
temp_F = np.copy(cube[4][:, 0])
temp_D = np.copy(cube[1][:, 0])
temp_B = np.copy(cube[5][:, 1])
cube[0][:, 0] = temp_B[::-1]
cube[4][:, 0] = temp_U
cube[1][:, 0] = temp_F
cube[5][:, 1] = temp_D[::-1]
return cube
def L_inv(cube):
cube[2] = np.rot90(cube[2], 1)
temp_U = np.copy(cube[0][:, 0])
temp_F = np.copy(cube[4][:, 0])
temp_D = np.copy(cube[1][:, 0])
temp_B = np.copy(cube[5][:, 1])
cube[0][:, 0] = temp_F
cube[4][:, 0] = temp_D
cube[1][:, 0] = temp_B[::-1]
cube[5][:, 1] = temp_U[::-1]
return cube
def U(cube):
cube[0] = np.rot90(cube[0], -1)
temp_F = np.copy(cube[4][0, :])
temp_R = np.copy(cube[3][0, :])
temp_B = np.copy(cube[5][0, :])
temp_L = np.copy(cube[2][0, :])
cube[4][0, :] = temp_L
cube[3][0, :] = temp_F
cube[5][0, :] = temp_R
cube[2][0, :] = temp_B
return cube
def U_inv(cube):
cube[0] = np.rot90(cube[0], 1)
temp_F = np.copy(cube[4][0, :])
temp_R = np.copy(cube[3][0, :])
temp_B = np.copy(cube[5][0, :])
temp_L = np.copy(cube[2][0, :])
cube[4][0, :] = temp_R
cube[3][0, :] = temp_B
cube[5][0, :] = temp_L
cube[2][0, :] = temp_F
return cube
def B(cube):
cube[5] = np.rot90(cube[5], -1)
temp_U = np.copy(cube[0][0, :])
temp_R = np.copy(cube[3][:, 1])
temp_D = np.copy(cube[1][1, :])
temp_L = np.copy(cube[2][:, 0])
cube[0][0, :] = temp_R
cube[3][:, 1] = temp_D[::-1]
cube[1][1, :] = temp_L
cube[2][:, 0] = temp_U[::-1]
return cube
def B_inv(cube):
cube[5] = np.rot90(cube[5], 1)
temp_U = np.copy(cube[0][0, :])
temp_R = np.copy(cube[3][:, 1])
temp_D = np.copy(cube[1][1, :])
temp_L = np.copy(cube[2][:, 0])
cube[0][0, :] = temp_L[::-1]
cube[3][:, 1] = temp_U
cube[1][1, :] = temp_R[::-1]
cube[2][:, 0] = temp_D
return cube
def D(cube):
cube[1] = np.rot90(cube[1], -1)
temp_F = np.copy(cube[4][1, :])
temp_R = np.copy(cube[3][1, :])
temp_B = np.copy(cube[5][1, :])
temp_L = np.copy(cube[2][1, :])
cube[4][1, :] = temp_L
cube[3][1, :] = temp_F
cube[5][1, :] = temp_R
cube[2][1, :] = temp_B
return cube
def D_inv(cube):
cube[1] = np.rot90(cube[1], 1)
temp_F = np.copy(cube[4][1, :])
temp_R = np.copy(cube[3][1, :])
temp_B = np.copy(cube[5][1, :])
temp_L = np.copy(cube[2][1, :])
cube[4][1, :] = temp_R
cube[3][1, :] = temp_B
cube[5][1, :] = temp_L
cube[2][1, :] = temp_F
return cube
def R(cube):
cube[3] = np.rot90(cube[3], -1)
temp_U = np.copy(cube[0][:, 1])
temp_F = np.copy(cube[4][:, 1])
temp_D = np.copy(cube[1][:, 1])
temp_B = np.copy(cube[5][:, 0])
cube[0][:, 1] = temp_B[::-1]
cube[4][:, 1] = temp_U
cube[1][:, 1] = temp_F
cube[5][:, 0] = temp_D[::-1]
return cube
def R_inv(cube):
cube[3] = np.rot90(cube[3], 1)
temp_U = np.copy(cube[0][:, 1])
temp_F = np.copy(cube[4][:, 1])
temp_D = np.copy(cube[1][:, 1])
temp_B = np.copy(cube[5][:, 0])
cube[0][:, 1] = temp_F
cube[4][:, 1] = temp_D
cube[1][:, 1] = temp_B[::-1]
cube[5][:, 0] = temp_U[::-1]
return cube
def test_rotation(func, initial_state):
state = initial_state.copy()
for _ in range(4):
state = func(state)
return np.array_equal(state, initial_state)
# Rubik's Cube 2x2 en une seule liste
initial_state = np.array([
[['w', 'w'], ['w', 'w']], # U
[['y', 'y'], ['y', 'y']], # D
[['g', 'g'], ['g', 'g']], # L
[['b', 'b'], ['b', 'b']], # R
[['r', 'r'], ['r', 'r']], # F
[['o', 'o'], ['o', 'o']] # B
])
affichage(initial_state)
#affichage(F(initial_state))
def test_rotation(func, initial_state):
state = initial_state.copy()
for _ in range(4):
state = func(state)
return np.array_equal(state, initial_state)
print("4*F = id ?", test_rotation(F, initial_state))
print("4*F_inv = id ?", test_rotation(F_inv, initial_state))
print("4*L = id ?", test_rotation(L, initial_state))
print("4*L_inv = id ?", test_rotation(L_inv, initial_state))
print("4*U = id ?", test_rotation(U, initial_state))
print("4*U_inv = id ?", test_rotation(U_inv, initial_state))
print("4*B = id ?", test_rotation(B, initial_state))
print("4*B_inv = id ?", test_rotation(B_inv, initial_state))
print("4*R = id ?", test_rotation(R, initial_state))
print("4*R_inv = id ?", test_rotation(R_inv, initial_state))
print("4*D = id ?", test_rotation(D, initial_state))
print("4*D_inv = id ?", test_rotation(D_inv, initial_state))
print()
def test_rotation3(func,func2, initial_state):
state = initial_state.copy()
for _ in range(3):
state = func(state)
return np.array_equal(state, func2(initial_state))
print("3*F = F_inv ?", test_rotation3(F, F_inv,initial_state))
print("3*L = L_inv ?", test_rotation3(L, L_inv,initial_state))
print("3*B = B_inv ?", test_rotation3(B, B_inv,initial_state))
print("3*R = R_inv ?", test_rotation3(R, R_inv,initial_state))
print("3*U = U_inv ?", test_rotation3(R, R_inv,initial_state))
print("3*D = D_inv ?", test_rotation3(R, R_inv,initial_state))
print()
def test_inverse(func, func_inv, initial_state):
state = func(initial_state.copy())
state = func_inv(state)
return np.array_equal(state, initial_state)
print("F F_inv = id ?", test_inverse(F, F_inv, initial_state))
print("B B_inv = id ?", test_inverse(B, B_inv, initial_state))
print("R R_inv = id ?", test_inverse(R, R_inv, initial_state))
print("L L_inv = id ?", test_inverse(L, L_inv, initial_state))
print("U U_inv = id ?", test_inverse(U, U_inv, initial_state))
print("D D_inv = id ?", test_inverse(D, D_inv, initial_state))
print()
def is_solved(cube):
# Vérifie si chaque face du cube est d'une seule couleur
for face in cube:
if not np.all(face == face[0,0]):
return False
return True
def solve(r, moves, max_depth, counter):
counter[0] += 1 # Augmenter le compteur à chaque appel
if is_solved(r):
return moves
if max_depth == 0:
return None
for move, func in [('F', F), ('F_inv', F_inv), ('B', B), ('B_inv', B_inv), ('R', R), ('R_inv', R_inv), ('L', L), ('L_inv', L_inv), ('U', U), ('U_inv', U_inv), ('D', D), ('D_inv', D_inv)]:
new_r = func(r.copy())
new_moves = moves + [move]
solution = solve(new_r, new_moves, max_depth-1, counter)
if solution:
return solution
return None
def apply_moves_to_state(moves, initial_state):
current_state = initial_state.copy()
for move in moves:
if move == 'F':
current_state = F(current_state)
elif move == 'F_inv':
current_state = F_inv(current_state)
elif move == 'B':
current_state = B(current_state)
elif move == 'B_inv':
current_state = B_inv(current_state)
elif move == 'R':
current_state = R(current_state)
elif move == 'R_inv':
current_state = R_inv(current_state)
elif move == 'L':
current_state = L(current_state)
elif move == 'L_inv':
current_state = L_inv(current_state)
elif move == 'U':
current_state = U(current_state)
elif move == 'U_inv':
current_state = U_inv(current_state)
elif move == 'D':
current_state = D(current_state)
elif move == 'D_inv':
current_state = D_inv(current_state)
return current_state
# Exemple d'utilisation :
start_time = time.time()
initial_state = np.array([
[['w', 'w'], ['w', 'w']], # U
[['y', 'y'], ['y', 'y']], # D
[['g', 'g'], ['g', 'g']], # L
[['b', 'b'], ['b', 'b']], # R
[['r', 'r'], ['r', 'r']], # F
[['o', 'o'], ['o', 'o']] # B
])
r = L(R(U(F(initial_state))))
affichage(r)
counter = [0] # Compteur pour stocker le nombre de coups essayés
for k in range(1,11):
solution = solve(r, [], k, counter)
if solution:
print("Solution brute trouvée:")
print(solution)
# Appliquer les mouvements de la solution pour vérifier
final_state = apply_moves_to_state(solution, r)
affichage(final_state)
break
else:
end_time = time.time()
elapsed_time = end_time - start_time
print(f"Temps écoulé : {elapsed_time:.5f} secondes")
print("Aucune solution trouvée dans la profondeur ",k," donnée.")
print("Nombre de coups essayés jusqu'à présent:", counter[0])
print()
end_time = time.time()
elapsed_time = end_time - start_time
print(f"Temps écoulé : {elapsed_time:.5f} secondes")
print("Nombre total de coups essayés:", counter[0])
Rudi's Cube 3x3 - récurcivité et force brute
import numpy as np
import time
# U pour "Up", D pour "Down", L pour "Left", R pour "Right", F pour "Front", B pour "Back"
# 'w' pour blanc, 'g' pour vert, 'r' pour rouge, 'b' pour bleu, 'o' pour orange, 'y' pour jaune
# F: Rotation de la face avant dans le sens horaire.
# B: Rotation de la face arrière dans le sens horaire.
# R: Rotation de la face droite dans le sens horaire.
# L: Rotation de la face gauche dans le sens horaire.
# U: Rotation de la face supérieure dans le sens horaire.
# D: Rotation de la face inférieure dans le sens horaire.
def affichage(cube):
# La face U (Up)
for row in cube[0]:
print(" ", end="")
print(" ".join(row))
print()
# Les faces L (Left), F (Front), R (Right), B (Back)
for i in range(3):
for face in [2, 4, 3, 5]:
print(" ".join(cube[face][i]), end=" ")
print()
print()
# La face D (Down)
for row in cube[1]:
print(" ", end="")
print(" ".join(row))
print()
# def rotate_face_90(face):
# """Fait pivoter une face de 90 degrés dans le sens horaire"""
# return np.rot90(face, -1)
def F(cube):
# Faire pivoter la face F elle-même
cube[4] = np.rot90(cube[4], -1)
# Sauvegarder les bords adjacents
temp_U = np.copy(cube[0][2])
temp_R = np.copy(cube[3][:, 0])
temp_D = np.copy(cube[1][0])
temp_L = np.copy(cube[2][:, 2])
# Mettre à jour les bords adjacents
cube[0][2] = temp_L[::-1]
cube[3][:, 0] = temp_U
cube[1][0] = temp_R[::-1]
cube[2][:, 2] = temp_D
return cube
def F_inv(cube):
# Faire pivoter la face F elle-même
cube[4] = np.rot90(cube[4], 1) # Rotation inverse
# Sauvegarder les bords adjacents
temp_U = np.copy(cube[0][2])
temp_R = np.copy(cube[3][:, 0])
temp_D = np.copy(cube[1][0])
temp_L = np.copy(cube[2][:, 2])
# Mettre à jour les bords adjacents
cube[0][2] = temp_R
cube[3][:, 0] = temp_D[::-1]
cube[1][0] = temp_L
cube[2][:, 2] = temp_U[::-1]
return cube
def L(cube):
# Faire pivoter la face L elle-même
cube[2] = np.rot90(cube[2], -1)
# Sauvegarder les bords adjacents
temp_U = np.copy(cube[0][:, 0])
temp_F = np.copy(cube[4][:, 0])
temp_D = np.copy(cube[1][:, 0])
temp_B = np.copy(cube[5][:, 2])
# Mettre à jour les bords adjacents
cube[0][:, 0] = temp_F
cube[4][:, 0] = temp_D
cube[1][:, 0] = temp_B[::-1]
cube[5][:, 2] = temp_U[::-1]
return cube
def L_inv(cube):
# Faire pivoter la face L elle-même
cube[2] = np.rot90(cube[2], 1) # Rotation dans le sens des aiguilles d'une montre
# Sauvegarder les bords adjacents
temp_U = np.copy(cube[0][:, 0])
temp_F = np.copy(cube[4][:, 0])
temp_D = np.copy(cube[1][:, 0])
temp_B = np.copy(cube[5][:, 2])
# Mettre à jour les bords adjacents
cube[0][:, 0] = temp_B[::-1]
cube[4][:, 0] = temp_U
cube[1][:, 0] = temp_F
cube[5][:, 2] = temp_D[::-1]
return cube
def U(cube):
# Faire pivoter la face U elle-même
cube[0] = np.rot90(cube[0], -1)
# Sauvegarder les bords adjacents
temp_F = np.copy(cube[4][0, :])
temp_R = np.copy(cube[3][0, :])
temp_B = np.copy(cube[5][0, :])
temp_L = np.copy(cube[2][0, :])
# Mettre à jour les bords adjacents
cube[4][0, :] = temp_L
cube[3][0, :] = temp_F
cube[5][0, :] = temp_R
cube[2][0, :] = temp_B
return cube
def U_inv(cube):
# Faire pivoter la face U elle-même
cube[0] = np.rot90(cube[0], 1)
# Sauvegarder les bords adjacents
temp_F = np.copy(cube[4][0, :])
temp_R = np.copy(cube[3][0, :])
temp_B = np.copy(cube[5][0, :])
temp_L = np.copy(cube[2][0, :])
# Mettre à jour les bords adjacents
cube[4][0, :] = temp_R
cube[3][0, :] = temp_B
cube[5][0, :] = temp_L
cube[2][0, :] = temp_F
return cube
def B(cube):
# Faire pivoter la face B elle-même
cube[5] = np.rot90(cube[5], -1)
# Sauvegarder les bords adjacents
temp_U = np.copy(cube[0][0, :])
temp_R = np.copy(cube[3][:, 2])
temp_D = np.copy(cube[1][2, :])
temp_L = np.copy(cube[2][:, 0])
# Mettre à jour les bords adjacents
cube[0][0, :] = temp_R[::-1]
cube[3][:, 2] = temp_D
cube[1][2, :] = temp_L[::-1]
cube[2][:, 0] = temp_U
return cube
def B_inv(cube):
# Faire pivoter la face B elle-même
cube[5] = np.rot90(cube[5], 1) # Rotation dans le sens des aiguilles d'une montre
# Sauvegarder les bords adjacents
temp_U = np.copy(cube[0][0, :])
temp_R = np.copy(cube[3][:, 2])
temp_D = np.copy(cube[1][2, :])
temp_L = np.copy(cube[2][:, 0])
# Mettre à jour les bords adjacents
cube[0][0, :] = temp_L
cube[3][:, 2] = temp_U[::-1]
cube[1][2, :] = temp_R
cube[2][:, 0] = temp_D[::-1]
return cube
def D(cube):
# Faire pivoter la face D elle-même
cube[1] = np.rot90(cube[1], -1)
# Sauvegarder les bords adjacents
temp_F = np.copy(cube[4][2, :])
temp_R = np.copy(cube[3][2, :])
temp_B = np.copy(cube[5][2, :])
temp_L = np.copy(cube[2][2, :])
# Mettre à jour les bords adjacents
cube[4][2, :] = temp_L
cube[3][2, :] = temp_F
cube[5][2, :] = temp_R
cube[2][2, :] = temp_B
return cube
def D_inv(cube):
# Faire pivoter la face D elle-même
cube[1] = np.rot90(cube[1], 1)
# Sauvegarder les bords adjacents
temp_F = np.copy(cube[4][2, :])
temp_R = np.copy(cube[3][2, :])
temp_B = np.copy(cube[5][2, :])
temp_L = np.copy(cube[2][2, :])
# Mettre à jour les bords adjacents
cube[4][2, :] = temp_R
cube[3][2, :] = temp_B
cube[5][2, :] = temp_L
cube[2][2, :] = temp_F
return cube
def R(cube):
# Faire pivoter la face R elle-même
cube[3] = np.rot90(cube[3], -1)
# Sauvegarder les bords adjacents
temp_U = np.copy(cube[0][:, 2])
temp_F = np.copy(cube[4][:, 2])
temp_D = np.copy(cube[1][:, 2])
temp_B = np.copy(cube[5][:, 0])
# Mettre à jour les bords adjacents
cube[0][:, 2] = temp_F
cube[4][:, 2] = temp_D
cube[1][:, 2] = temp_B[::-1]
cube[5][:, 0] = temp_U[::-1]
return cube
def R_inv(cube):
# Faire pivoter la face R elle-même
cube[3] = np.rot90(cube[3], 1)
# Sauvegarder les bords adjacents
temp_U = np.copy(cube[0][:, 2])
temp_F = np.copy(cube[4][:, 2])
temp_D = np.copy(cube[1][:, 2])
temp_B = np.copy(cube[5][:, 0])
# Mettre à jour les bords adjacents
cube[0][:, 2] = temp_B[::-1]
cube[4][:, 2] = temp_U
cube[1][:, 2] = temp_F
cube[5][:, 0] = temp_D[::-1]
return cube
def test_rotation(func, initial_state):
state = initial_state.copy()
for _ in range(4):
state = func(state)
return np.array_equal(state, initial_state)
# Rubik's Cube 2x2 en une seule liste
initial_state = np.array([
[['w', 'w', 'w'], ['w', 'w', 'w'], ['w', 'w', 'w']], # U
[['y', 'y', 'y'], ['y', 'y', 'y'], ['y', 'y', 'y']], # D
[['g', 'g', 'g'], ['g', 'g', 'g'], ['g', 'g', 'g']], # L
[['b', 'b', 'b'], ['b', 'b', 'b'], ['b', 'b', 'b']], # R
[['r', 'r', 'r'], ['r', 'r', 'r'], ['r', 'r', 'r']], # F
[['o', 'o', 'o'], ['o', 'o', 'o'], ['o', 'o', 'o']] # B
])
affichage(initial_state)
#affichage(F(initial_state))
def test_rotation(func, initial_state):
state = initial_state.copy()
for _ in range(4):
state = func(state)
return np.array_equal(state, initial_state)
print("4*F = id ?", test_rotation(F, initial_state))
print("4*F_inv = id ?", test_rotation(F_inv, initial_state))
print("4*L = id ?", test_rotation(L, initial_state))
print("4*L_inv = id ?", test_rotation(L_inv, initial_state))
print("4*B = id ?", test_rotation(B, initial_state))
print("4*B_inv = id ?", test_rotation(B_inv, initial_state))
print("4*R = id ?", test_rotation(R, initial_state))
print("4*R_inv = id ?", test_rotation(R_inv, initial_state))
print("4*U = id ?", test_rotation(U, initial_state))
print("4*U_inv = id ?", test_rotation(U_inv, initial_state))
print("4*D = id ?", test_rotation(D, initial_state))
print("4*D_inv = id ?", test_rotation(D_inv, initial_state))
print()
def test_rotation3(func,func2, initial_state):
state = initial_state.copy()
for _ in range(3):
state = func(state)
return np.array_equal(state, func2(initial_state))
print("3*F = F_inv ?", test_rotation3(F, F_inv,initial_state))
print("3*L = L_inv ?", test_rotation3(L, L_inv,initial_state))
print("3*B = B_inv ?", test_rotation3(B, B_inv,initial_state))
print("3*R = R_inv ?", test_rotation3(R, R_inv,initial_state))
print("3*U = U_inv ?", test_rotation3(R, R_inv,initial_state))
print("3*D = D_inv ?", test_rotation3(R, R_inv,initial_state))
print()
def test_inverse(func, func_inv, initial_state):
state = func(initial_state.copy())
state = func_inv(state)
return np.array_equal(state, initial_state)
print("F F_inv = id ?", test_inverse(F, F_inv, initial_state))
print("B B_inv = id ?", test_inverse(B, B_inv, initial_state))
print("R R_inv = id ?", test_inverse(R, R_inv, initial_state))
print("L L_inv = id ?", test_inverse(L, L_inv, initial_state))
print("U U_inv = id ?", test_inverse(U, U_inv, initial_state))
print("D D_inv = id ?", test_inverse(D, D_inv, initial_state))
print()
def is_solved(cube):
# Vérifie si chaque face du cube est d'une seule couleur
for face in cube:
if not np.all(face == face[0,0]):
return False
return True
def solve(r, moves, max_depth, counter):
counter[0] += 1 # Augmenter le compteur à chaque appel
if is_solved(r):
return moves
if max_depth == 0:
return None
for move, func in [('F', F), ('F_inv', F_inv), ('B', B), ('B_inv', B_inv), ('R', R), ('R_inv', R_inv), ('L', L), ('L_inv', L_inv), ('U', U), ('U_inv', U_inv), ('D', D), ('D_inv', D_inv)]:
new_r = func(r.copy())
new_moves = moves + [move]
solution = solve(new_r, new_moves, max_depth-1, counter)
if solution:
return solution
return None
def apply_moves_to_state(moves, initial_state):
current_state = initial_state.copy()
for move in moves:
if move == 'F':
current_state = F(current_state)
elif move == 'F_inv':
current_state = F_inv(current_state)
elif move == 'B':
current_state = B(current_state)
elif move == 'B_inv':
current_state = B_inv(current_state)
elif move == 'R':
current_state = R(current_state)
elif move == 'R_inv':
current_state = R_inv(current_state)
elif move == 'L':
current_state = L(current_state)
elif move == 'L_inv':
current_state = L_inv(current_state)
elif move == 'U':
current_state = U(current_state)
elif move == 'U_inv':
current_state = U_inv(current_state)
elif move == 'D':
current_state = D(current_state)
elif move == 'D_inv':
current_state = D_inv(current_state)
return current_state
# Exemple d'utilisation :
start_time = time.time()
initial_state = np.array([
[['w', 'w', 'w'], ['w', 'w', 'w'], ['w', 'w', 'w']], # U
[['y', 'y', 'y'], ['y', 'y', 'y'], ['y', 'y', 'y']], # D
[['g', 'g', 'g'], ['g', 'g', 'g'], ['g', 'g', 'g']], # L
[['b', 'b', 'b'], ['b', 'b', 'b'], ['b', 'b', 'b']], # R
[['r', 'r', 'r'], ['r', 'r', 'r'], ['r', 'r', 'r']], # F
[['o', 'o', 'o'], ['o', 'o', 'o'], ['o', 'o', 'o']] # B
])
r = R(D(L(R(U(F(initial_state))))))
affichage(r)
counter = [0] # Compteur pour stocker le nombre de coups essayés
for k in range(1,21):
solution = solve(r, [], k, counter)
if solution:
print("Solution brute trouvée:")
print(solution)
# Appliquer les mouvements de la solution pour vérifier
final_state = apply_moves_to_state(solution, r)
# Votre code pour afficher le cube ici
break
else:
end_time = time.time()
elapsed_time = end_time - start_time
print(f"Temps écoulé : {elapsed_time:.5f} secondes")
print("Aucune solution trouvée dans la profondeur ",k," donnée.")
print("Nombre de coups essayés jusqu'à présent:", counter[0])
print()
end_time = time.time()
elapsed_time = end_time - start_time
print(f"Temps écoulé : {elapsed_time:.5f} secondes")
print("Nombre total de coups essayés:", counter[0])
01 - POO, Piles, Files, Listes, Dictionnaires
Fiche de Révision : POO, Piles, Files, Listes, Dictionnaires - Tle NSI
1. Interface, Implémentation, POO
Concepts clés :
- Interface : Définit les fonctionnalités d'une classe ou d'un module, sans implémentation spécifique.
- Implémentation : La réalisation concrète des fonctionnalités définies par l'interface.
- Encapsulation : Principe de protection des données internes d'une classe en utilisant des attributs privés et des méthodes publiques pour y accéder.
- Héritage : Permet à une classe de réutiliser et d'étendre les fonctionnalités d'une autre classe.
- Polymorphisme : Capacité à utiliser une interface unique pour des types différents, par exemple via des méthodes redéfinies.
class Voiture: # Classe structure qui permet de définir des objets qui encapsulent des données et des fonctions.
def __init__(self, marque, modele, kilometrage):# Constructeur, et self fait référence à l'instance actuelle.
self.marque = marque # Attribut
self.modele = modele # Attribut
self.kilometrage = kilometrage # Attribut interne de l'objet ou de l'instance
def afficher_details(self): # Méthode
print(f"Voiture {self.marque} {self.modele}, {self.kilometrage} km parcourus.")
def conduire(self, km): # Méthode
self.kilometrage += km
# Exemple
v1 = Voiture("Peugeot", "208", 10000) # Création d'une instance de la classe.
v1.afficher_details()
v1.conduire(150)
v1.afficher_details()
v2 = Voiture("Tesla", "Modèle 3", 60000) # Création d'une autre instance de la classe.
v2.afficher_details()Voiture Peugeot 208, 10000 km parcourus. Voiture Peugeot 208, 10150 km parcourus. Voiture Tesla Modèle 3, 60000 km parcourus.
2. Piles, Files, Listes
Concepts clés :
- Pile (LIFO) : Dernier entré, premier sorti (Last In, First Out).
- File (FIFO) : Premier entré, premier sorti (First In, First Out).
- Liste : Structure de données linéaire dynamique permettant l'accès, l'insertion et la suppression à n'importe quelle position.
# Exemple de pile en Python
pile = []
pile.append(10)
pile.append(20)
pile.append(30)
print(pile) # Affiche [10, 20, 30]
print(pile.pop()) # Retire 30
print(pile) # Affiche [10, 20][10, 20, 30] 30 [10, 20]
# Exemple de file en Python
file = []
file.append(10)
file.append(20)
file.append(30)
print(file) # Affiche [10, 20,30]
print(file.pop(0)) # Retire 10
print(file) # Affiche [20, 30][10, 20, 30] 10 [20, 30]
3. Dictionnaires
Concepts clés :
- Structure de données non ordonnée basée sur des paires clé-valeur.
- Complexité moyenne des opérations (recherche, insertion, suppression) : 𝑂(1).
- Permet un accès rapide aux éléments via leurs clés.
# Exemple de dictionnaire en Python
dictionnaire = {'a': 1, 'b': 2, 'c': 3}
print(dictionnaire['a']) # Accès à la valeur associée à la clé 'a'
dictionnaire['d'] = 4 # Ajout d'une nouvelle clé-valeur
del dictionnaire['b'] # Suppression de la clé 'b'
print(dictionnaire)1
{'a': 1, 'c': 3, 'd': 4}
# Exemple mettant en œuvre les trois types de boucle for sur un dictionnaire
dictionnaire = {'a': 1, 'b': 2, 'c': 3}
# Boucle sur les clés
print("Parcours des clés :")
for cle in dictionnaire:
print(f"Clé : {cle}")
# Boucle sur les valeurs
print("\nParcours des valeurs :")
for valeur in dictionnaire.values():
print(f"Valeur : {valeur}")
# Boucle sur les paires clé-valeur
print("\nParcours des paires clé-valeur :")
for cle, valeur in dictionnaire.items():
print(f"Clé : {cle}, Valeur : {valeur}")02 - Arbre
Fiche de Révision : Les Arbres - Terminale NSI
Concepts de base sur les arbres
Un arbre est une structure de données hiérarchique constituée de nœuds reliés par des arêtes. Les arbres sont utilisés pour modéliser des relations de type parent-enfant.
Définitions :
- Racine : Le nœud de départ de l’arbre, qui n’a pas de parent.
- Nœud : Un élément de l’arbre contenant des données.
- Feuille : Un nœud sans enfant.
- Arête : La connexion entre deux nœuds.
- Sous-arbre : Une partie d’un arbre représentée par un nœud et ses descendants.
Arbres binaires
Un arbre binaire est un arbre dans lequel chaque nœud peut avoir au plus deux enfants.
Un arbre binaire de recherche (ABR) est un arbre binaire avec les propriétés suivantes :
-
Les nœuds dans le sous-arbre gauche ont une valeur inférieure au nœud parent.
-
Les nœuds dans le sous-arbre droit ont une valeur supérieure au nœud parent.
40 / \ 20 60 / \ / \ 10 30 50 70
class Noeud:
def __init__(self, valeur, gauche=None, droit=None):
self.valeur = valeur
self.gauche = gauche
self.droit = droit
# Exemple d’arbre binaire
racine = Noeud(40, Noeud(20, Noeud(10), Noeud(30)), Noeud(60, Noeud(50), Noeud(70)))
# autre méthode pour implémenter l'arbre en initialisant chaque nœud étape par étape
n10 = Noeud(10)
n30 = Noeud(30)
n20 = Noeud(20, n10, n30)
n50 = Noeud(50)
n70 = Noeud(70)
n60 = Noeud(60, n50, n70)
racine = Noeud(40, n20, n60)Définitions Métriques :
- La taille de l'arbre est le nombre total de nœuds.
- La hauteur de l'arbre est le nombre d'arêtes de la racine au nœud le plus profond .
- La profondeur d'un nœud est le nombre d'arêtes de la racine à ce nœud.
def taille_arbre(noeud):
if noeud is None:
return 0
return 1 + taille_arbre(noeud.gauche) + taille_arbre(noeud.droit)
def hauteur_arbre(noeud):
if noeud is None:
return -1
return 1 + max(hauteur_arbre(noeud.gauche), hauteur_arbre(noeud.droit))
print("Taille de l’arbre :", taille_arbre(racine))
print("Hauteur de l’arbre :", hauteur_arbre(racine))Taille de l’arbre : 7 Hauteur de l’arbre : 2
Parcours des arbres
Types de parcours :
- Préfixe (préordre) : Racine → Gauche → Droite
- Infixe (inordre) : Gauche → Racine → Droite
- Suffixe (postordre) : Gauche → Droite → Racine
- Largeur d'abord : Niveau par niveau, de gauche à droite.
def parcours_prefixe(noeud):
if noeud is not None:
return [noeud.valeur] + parcours_prefixe(noeud.gauche) + parcours_prefixe(noeud.droit)
else:
return []
def parcours_infixe(noeud):
if noeud is not None:
return parcours_infixe(noeud.gauche) + [noeud.valeur] + parcours_infixe(noeud.droit)
else:
return []
def parcours_suffixe(noeud):
if noeud is not None:
return parcours_suffixe(noeud.gauche) + parcours_suffixe(noeud.droit) + [noeud.valeur]
else:
return []
# Résultats des parcours
print("Parcours préfixe :", parcours_prefixe(racine))
print("Parcours infixe :", parcours_infixe(racine))
print("Parcours suffixe :", parcours_suffixe(racine))Parcours préfixe : [40, 20, 10, 30, 60, 50, 70] Parcours infixe : [10, 20, 30, 40, 50, 60, 70] Parcours suffixe : [10, 30, 20, 50, 70, 60, 40]
def parcours_largeur(racine):
if not racine:
return []
file = [racine]
resultat = []
while file:
noeud = file.pop(0) # Récupère le premier élément de la file
resultat.append(noeud.valeur)
if noeud.gauche:
file.append(noeud.gauche)
if noeud.droit:
file.append(noeud.droit)
return resultat
# Exemple d'utilisation
print("Parcours largeur :",parcours_largeur(racine))Parcours largeur : [40, 20, 60, 10, 30, 50, 70]
Arbres binaires de recherche : Recherche et insertion
Recherche dans un ABR :
def rechercher(noeud, valeur):
if noeud is None:
return False
if noeud.valeur == valeur:
return True
if valeur < noeud.valeur:
return rechercher(noeud.gauche, valeur)
return rechercher(noeud.droit, valeur)
print("Recherche 30 :", rechercher(racine, 30))
print("Recherche 100 :", rechercher(racine, 100))Recherche 30 : True Recherche 100 : False
Insertion dans un ABR :
def inserer(noeud, valeur):
if noeud is None:
return Noeud(valeur)
if valeur < noeud.valeur:
noeud.gauche = inserer(noeud.gauche, valeur)
else:
noeud.droit = inserer(noeud.droit, valeur)
return noeud
racine = inserer(racine, 35)
print("Recherche 35 après insertion :", rechercher(racine, 35))Recherche 35 après insertion : True
Arbres équilibrés (AVL)
Les arbres AVL sont des arbres binaires de recherche auto-équilibrés qui maintiennent une hauteur logarithmique, garantissant des opérations efficaces.
Propriétés : Complexité temporelle de recherche
La recherche dans un arbre AVL est de complexité 𝑂(𝑙𝑜𝑔(𝑛)), où 𝑛 est le nombre de nœuds dans l'arbre.
Si un arbre binaire de recherche n'est pas équilibré (par exemple, une structure en ligne droite), la complexité de recherche peut se dégrader vers 𝑂(𝑛) dans le pire des cas.
03 - Graphe
Fiche de Révision : Graphes - NSI Terminale
Concepts Essentiels des Graphes
Définitions
- Sommet : Un point dans le graphe (nœud).
- Arête : Une connexion entre deux sommets.
Orientée : Elle a une direction.
Non-orientée : Elle n'a pas de direction. - Graphe pondéré : Les arêtes ont un poids (ou coût).
- Connexité : Un graphe est
connexesi n'importe quelle paire de sommets peut toujours être reliée par une chaîne. - Matrice d'adjacence : On représente les arêtes dans une matrice, c'est-à-dire un tableau à deux dimensions où on inscrit le poids en ligne i et colonne j de l'arête du sommets de rang i vers de rang j.
- Liste de successeurs : Liste des sommets accessibles depuis un sommet donné.
- Liste de prédécesseurs : Liste des sommets qui pointent vers un sommet donné.
Exemple

import numpy as np
class Graphe_Matrice_Adjacente:
def __init__(self, matrice_adjacence, noms_sommets):
self.matrice_adjacence = np.array(matrice_adjacence)
self.noms_sommets = noms_sommets
def liste_successeurs(self):
liste_succ = {}
n = len(self.matrice_adjacence)
for i in range(n):
successeurs = []
for j in range(n):
if self.matrice_adjacence[i][j]:
successeurs.append(self.noms_sommets[j])
liste_succ[self.noms_sommets[i]] = successeurs
return liste_succ
# Création d'un graphe avec la matrice d'adjacence donnée
matrice_adjacence = [[ 0, 7, 12, 0, 0],
[ 7, 0, 4, 8, 0],
[12, 4, 0, 13, 5],
[ 0, 8, 13, 0, 6],
[ 0, 0, 5, 6, 0] ]
noms_sommets = ['A', 'B', 'C', 'D', 'E']
# Instanciation de la classe Graphe_Matrice_Adjacente
graphe = Graphe_Matrice_Adjacente(matrice_adjacence, noms_sommets)
print("Liste des successeurs :",graphe.liste_successeurs())Liste des successeurs : {'A': ['B', 'C'], 'B': ['A', 'C', 'D'], 'C': ['A', 'B', 'D', 'E'], 'D': ['B', 'C', 'E'], 'E': ['C', 'D']}
Algorithmes Importants sur les Graphes
DFS (Depth-First Search), traduit en français par "Parcours en profondeur d'abord", consiste à explorer un graphe en allant aussi loin que possible dans une branche avant de revenir en arrière pour explorer les voisins restants. Ce type de parcours ne tient pas compte des poids des arêtes : il se concentre sur le premier voisin non visité, qui à son tour procède de la même manière, jusqu'à ce qu'il n'y ait plus de voisins non explorés.
BFS (Breadth-First Search), traduit en français par "Parcours en largeur", explore tous les nœuds voisins d'un nœud avant de passer au niveau suivant. Ce type de parcours ignore également les poids des arêtes, mais il permet de trouver le plus court chemin entre deux nœuds en supposant que chaque arête a un poids égal à 1.
def DFS(graph,debut):
result = []
a_visite = [debut]
while a_visite:
noeux=a_visite.pop(0)
if noeux not in result:
result.append(noeux)
a_visite = graph[noeux] + a_visite
return result
def BFS(graph,debut):
result = []
a_visite = [debut]
while a_visite:
noeux = a_visite.pop(0)
if noeux not in result:
result.append(noeux)
a_visite = a_visite + graph[noeux]
return result
# Exemple de graphe
graph_successeurs = {'A': ['B', 'C', 'D'],
'B': ['A', 'E', 'F'],
'C': ['A', 'G', 'H'],
'D': ['A'],
'E': ['B'],
'F': ['B'],
'G': ['C', 'H'],
'H': ['C', 'G']}
print("Ordre de visite DFS :", DFS(graph_successeurs, 'A'))
print("Ordre de visite BFS :", BFS(graph_successeurs, 'A'))Ordre de visite DFS : ['A', 'B', 'E', 'F', 'C', 'G', 'H', 'D'] Ordre de visite BFS : ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
04 - SQL
Fiche de Révision : SQL - Terminale NSI
Partie 1 : Modèle Relationnel
Concepts principaux
- Relation : Une table dans une base de données.
- Attribut : Une colonne d'une table (propriété des données).
- Domaine : Ensemble de valeurs admissibles pour un attribut.
- Clé primaire : Identifiant unique d'une ligne dans une table.
- Clé étrangère : Attribut établissant un lien avec une clé primaire d'une autre table.
Exemple de schéma relationnel
AUTEURS(id : INT, nom : TEXT, prenom : TEXT, ann_naissance : INT, langue_ecriture : TEXT)
LIVRES(id : INT, titre : TEXT, #id_auteur : INT, ann_publi : INT, note : INT)
Les attributs soulignés sont des clés primaires, le # signifie que l'on a une clé étrangère.
Partie 2 : Requêtes SQL
1. Requêtes de sélection
- Afficher tous les attributs :
SELECT * FROM LIVRES; - Afficher certains attributs :
SELECT titre, note FROM LIVRES;
2. Conditionner les résultats avec WHERE
- Exemple :
SELECT titre FROM LIVRES WHERE note > 9;
3. Trier les résultats avec ORDER BY
- Croissant :
SELECT titre, ann_publi FROM LIVRES ORDER BY ann_publi; - Décroissant :
SELECT titre, ann_publi FROM LIVRES ORDER BY ann_publi DESC;
4. Éviter les doublons avec DISTINCT
-
Exemple :
SELECT DISTINCT langue_ecriture FROM AUTEURS;5. Jointures
-
Associer deux tables avec une jointure interne (
INNER JOIN) :SELECT LIVRES.titre, AUTEURS.nom FROM LIVRES INNER JOIN AUTEURS ON LIVRES.id_auteur = AUTEURS.id; -
Ajouter une condition avec
WHERE:SELECT LIVRES.titre, AUTEURS.nom FROM LIVRES INNER JOIN AUTEURS ON LIVRES.id_auteur = AUTEURS.id WHERE LIVRES.ann_publi > 1950;
6. Compter
SELECT COUNT(*)
FROM LIVRES
WHERE note > 9;7. Manipulations de données
Insérer des données
INSERT INTO LIVRES (id, titre, id_auteur, ann_publi, note)
VALUES (17, 'Hypérion', 11, 1989, 8);Mettre à jour des données
UPDATE LIVRES
SET note = 10
WHERE titre = 'Dune';Supprimer des données
DELETE FROM LIVRES
WHERE titre = 'Dune';Attention : Sans WHERE, toutes les données seront supprimées :
DELETE FROM LIVRES;05 - Routage
Fiche BAC : Routage - Terminale NSI
1. Adresses IP et sous-réseaux
Concepts clés :
- Adresse IP : Identifiant unique d'une machine dans un réseau (ex.
192.168.1.10). - Masque de sous-réseau : Sépare la partie réseau et la partie hôte d'une adresse IP (ex.
255.255.255.0). - Adresse réseau : Identifie le réseau auquel appartient une machine (ex. pour
192.168.1.10/24, l'adresse réseau est192.168.1.0). - Adresse de broadcast : Permet d'envoyer un message à toutes les machines du réseau (ex. pour
192.168.1.10/24, l'adresse de broadcast est192.168.1.255). - Notation CIDR (
/n) : Indique le nombre de bits utilisés pour la partie réseau dans le masque (ex./24équivaut à255.255.255.0).
Exemple :
- Adresse IP :
192.168.1.10/24- Adresse réseau :
192.168.1.0 - Masque de sous-réseau :
255.255.255.0 - Adresse de broadcast :
192.168.1.255 - Plage d'adresses disponibles :
192.168.1.1à192.168.1.254
- Adresse réseau :
2. Tables de routage
Les routeurs permettent d'aiguiller les paquets entre les différents réseaux.
Une table de routage contient les informations nécessaires pour choisir le chemin :
- Destination : Sous-réseau ou adresse IP cible.
- Interface : Par où sortent les données.
- Passerelle : Prochain routeur si nécessaire. Si aucune route spécifique n'est trouvée, une route par défaut peut être utilisée.
Exemple : Table de routage du serveur R1

| Destination | Interface | Passerelle |
|---|---|---|
| F | 192.168.0.254 | |
| A | 10.0.5.152 | |
| E | 172.17.1.254 | |
| B | 172.17.1.254 | 172.17.1.123 |
| C | 10.0.5.152 | 10.0.5.135 |
3. Protocole RIP (Routing Information Protocol)
- Fonctionne sur le principe de l'échange périodique de tables entre routeurs.
- Métrique : Nombre de sauts.
Règles du RIP :
- Ajoute une route si elle est inconnue.
- Met à jour une route si une distance plus courte est trouvée.
- Ignore une route plus longue.
- Si un routeur est inactif pendant 3 minutes, la distance devient infinie (16).
4. Protocole OSPF (Open Shortest Path First)
- Basé sur la connaissance globale du réseau.
- Métrique : Coût des liaisons, proportionnel à leur bande passante.
- Chemin optimal : Basé sur le coût minimal, pas uniquement le plus court.
Calcul du coût :
$coût = \frac{10^8}{débit}$ où $𝑑ébit$ est exprimé en bits/s
Rappel : 1 kbit = 1 000 bits ; 1Mbit = 1 000 kbits ; 1 Gbit = 1 000 Mbits
- Exemple : Pour un débit de 20 Mbps, $coût = \frac{10^8}{20 \times 10^6} = 5$.


Le chemin le plus rapide pour aller de l'ordinateur 192.168.0.5 au serveur 10.7.3.8 est donc R1-R2-R4 avec un coût de 4 + 2 + 2 +10 = 18 , et non R1-R3 comme l'aurait indiqué le protocole RIP.
06 - Récursivité et Diviser pour régner
Fiche de Révision : Récursivité et Diviser pour régner
1. La récursivité
Définition :
Une fonction récursive est une fonction qui s'appelle elle-même.
Structure d'une fonction récursive :
- Cas de base : Condition qui arrête la récursion.
- Appel récursif : Réduction du problème pour atteindre le cas de base.
Exemple : Calcul de la factorielle
def factorielle(n):
if n == 0: # Cas de base
return 1
else:
return n * factorielle(n - 1) # Appel récursif
print(factorielle(5)) # Résultat : 120120
Points à vérifier pour la récursivité :
- Existe-t-il un cas de base qui termine la récursion ?
- La réduction du problème est-elle correcte à chaque appel ?
Attention :
Par défaut, Python autorise un maximum d'environ 1000 appels récursifs (ce nombre peut varier en fonction de la plateforme).
2. Diviser pour régner
Définition :
Un algorithme « Diviser pour régner » divise un problème en sous-problèmes, les résout de manière indépendante, puis combine les résultats.
Étapes principales :
- Diviser : Fractionner le problème en sous-problèmes plus petits.
- Régner : Résoudre récursivement chaque sous-problème.
- Combiner : Fusionner les solutions des sous-problèmes.
Exemple : Tri fusion (_Merge Sort_)

def tri_fusion(liste):
if len(liste) <= 1: # Cas de base
return liste
# Diviser
milieu = len(liste) // 2
gauche = tri_fusion(liste[:milieu])
droite = tri_fusion(liste[milieu:])
# Combiner
return fusion(gauche, droite)
def fusion(gauche, droite):
resultat = []
while gauche and droite:
if gauche[0] < droite[0]:
resultat.append(gauche.pop(0))
else:
resultat.append(droite.pop(0))
resultat = resultat + (gauche or droite)
return resultat
# Exemple d'utilisation
print(tri_fusion([4, 3, 8, 2, 7, 1, 5])) # Résultat : [1, 2, 3, 4, 5, 7, 8][1, 2, 3, 4, 5, 7, 8]
07 - Système sur Puce et Processus Système
Fiche BAC : Système sur Puce et Processus/Système
1. Système sur Puce (SoC)
Définition :
Un Système sur Puce (System on Chip - SoC) intègre tous les composants nécessaires pour faire fonctionner un système informatique sur un seul circuit intégré.
Loi de Moore :
- Énoncé : La densité des transistors sur un circuit intégré double environ tous les 18 à 24 mois, augmentant ainsi les performances tout en réduisant le coût.
- Limites actuelles :
- Les dimensions physiques des transistors approchent de limites atomiques.
- Dissipation thermique et consommation énergétique accrues.
Exemple de SoC :
- Apple A15 Bionic : utilisé dans les iPhones.
- Snapdragon 8 Gen 1 : utilisé dans les smartphones Android haut de gamme.
2. Processus et Systèmes
Processus :
Un processus est un programme en cours d'exécution, comprenant :
- Espace mémoire : Code, données, pile.
- État : Actif, suspendu, ou terminé.
Threads :
- Sous-ensemble d'un processus permettant l'exécution simultanée de plusieurs tâches dans un même espace mémoire.
- Partagent les ressources du processus parent.
Interblocage (Deadlock) :
Un interblocage se produit lorsque plusieurs processus attendent indéfiniment qu'une ressource détenue par un autre processus soit libérée.
Conditions pour un interblocage :
- Exclusion mutuelle : Les ressources ne peuvent être utilisées que par un processus à la fois.
- Rétention et attente : Un processus retient une ressource tout en attendant d'autres ressources.
- Non-préemption : Les ressources ne peuvent pas être retirées de force.
- Attente circulaire : Les processus forment une chaîne circulaire d'attente de ressources.
08 - Modularité
Fiche de Révision : Modularité
1. Qu'est-ce que la modularité ?
- Définition : Décomposer un système complexe en modules gérant chacun une fonctionnalité spécifique.
- Avantages :
- Réutilisabilité : Modules utilisables dans plusieurs projets.
- Maintenabilité : Localisation rapide des erreurs.
- Extensibilité : Ajout ou modification facile de fonctionnalités.
- Compréhensibilité : Systèmes plus simples à analyser.
2. Modules Python
- Lister les contenus :
dir(nom_du_module) - Aide intégrée :
help(nom_du_module.élément) - Documentation : Accéder aux docstrings avec
élément.__doc__.
import math
dir(math)help(math.sin)Help on built-in function sin in module math:
sin(x, /)
Return the sine of x (measured in radians).
print(math.sin.__doc__)Return the sine of x (measured in radians).
3. Importations en Python
import module: Accès à toutes les fonctions avec la notation pointée (module.fonction()).from module import fonction: Accès direct à la fonction (fonction()).- *_`from module import _`** : Importe tout (déconseillé pour éviter les conflits de noms).
- Alias : Utilisez
aspour renommer un module ou une fonction.
import math
math.sqrt(2)from math import sqrt
sqrt(2)from math import *
sqrt(2)from math import sqrt as racine_carree
racine_carree(2)4. Créer un module
Exemple :
def addition(a, b):
"""
Retourne la somme de a et b.
"""
return a + bhelp(addition)Help on function addition in module __main__:
addition(a, b)
Retourne la somme de a et b.
09 - Tri par insertion, tri par selection
Fiche de Révision : Tri par insertion, tri par selection
Tri par insertion
def tri_insertion(tab):
n = len(tab)
for i in range(1, n):
valeur_insertion = tab[i]
j = i
while j > 0 and valeur_insertion < tab[j-1]:
tab[j] = tab[j-1]
j = j - 1
tab[j] = valeur_insertion
return tab
# Exemple d'utilisation
tab = [4, 3, 5, 1]
print("Tableau trié:",tri_insertion(tab) )Tableau trié: [1, 3, 4, 5]
Tri par sélection
def tri_selection(tab):
for i in range(len(tab)):
min_i = i
for j in range(i+1, len(tab)):
if tab[min_i] > tab[j]:
min_i = j
tab[i], tab[min_i] = tab[min_i], tab[i]
# Exemple d'utilisation
tab = [12, 11, 13, 5, 6]
tri_selection(tab)
print("Tableau trié:", tab)Tableau trié: [5, 6, 11, 12, 13]
Coût des algorithmes de tris par insertion, et par sélection
Les algorithmes de tris par insertion, par sélection ont un coût O($n^2$), où $n$ est la taille du tableau.
Cela signifie que le temps d'exécution augmente de manière quadratrique avec le nombre d'éléments dans le tableau.
Démonstration :
Comme chaque boucle interne peut prendre jusqu'à $n$ itérations et il y a $n$ boucles externes, cela donne un total de $n×n=n^2$ opérations dans le pire cas.
10 - Les congruences
Les congruences

Théorème de Bézout :
Si a et b sont des entiers non nuls, alors il existe des entiers relatifs x et y, et un entier d tels que ax + by = d où d est le PGCD de a et b.
Algorithme d'Euclide (Classe de 3ième) ou PGCD de a et b
PDCD(a,b) = ?
1er cas : si b = 0
PDCD(a,b) = PDCD(a,0) = a
2ième Cas : si b > 0
Posons a = qb + r où q est le quotient et r est le reste de la division euclidienne de a par b.
d = PGCD(a,b) = PGCD(b,r)
def pgcd(a, b):
if b == 0:
return a
else:
return pgcd(b, a % b)
# Exemple d'utilisation
a = 91
b = 77
print("Le PGCD de", a, "et", b, "est :", pgcd(a, b))Le PGCD de 91 et 77 est : 7
Algorithme d'Euclide étendu ou comment trouver des coefficients x et y de Bezout et le PDCD de a et b
1er cas : si b = 0
d =a, x = 1, y = 0 est une solution de ax + by = d
2ième Cas : si b > 0
ax + by = d <=> (qb + r)x + by = d <=> b(qx + y) + rx = d <=> bx1 + ry1 = d avec x1 = qx + y et y1 = x <=> bx1 + ry1 = d avec x = y1 et y = x1 - qy1
def euclide_etendu(a, b):
if b == 0:
return a, 1, 0
else:
pgcd, x1, y1 = euclide_etendu(b, a % b)
x = y1
y = x1 - (a // b) * y1
return pgcd, x, y
# Exemple d'utilisation
a = 91
b = 77
pgcd, x, y = euclide_etendu(a, b)
print(f"Une solution de {a}x + {b}y = d est {a}({x}) + {b}({y}) = {pgcd}.")Une solution de 91x + 77y = d est 91(-5) + 77(6) = 7.
Théorème de Gauss :
Si a, b et c sont des entiers non nuls.
Si a divise le produit bc et si a et b sont premiers entre eux alors a divise c.
Définition de la Congruence :
Soient a, b, n des entiers relatifs.
On dit que a est congruent à b modulo n, noté a≡b (mod n) ou a≡b[n], si n divise la différence a−b.
Propriétés des Propriétés de Congruence :
- Réflexivité : Pour tout entier relatif a, a ≡ a [n].
- Symétrie : Si a et b sont des entiers relatifs et a ≡ b [n], alors b ≡ a [n].
- Transitivité : Si a, b, et c sont des entiers relatifs et a ≡ b [n] et b ≡ c [n], alors a ≡ c [n].
- Addition : Si a, b, c, et d sont des entiers relatifs et a ≡ b [n] et c ≡ d [n], alors a + c ≡ b + d [n].
- Soustraction : Si a, b, c, et d sont des entiers relatifs et a ≡ b [n] et c ≡ d [n], alors a - c ≡ b - d [n].
- Multiplication : Si a, b, c, et d sont des entiers relatifs et a ≡ b [n] et c ≡ d [n], alors a * c ≡ b * d [n].
- Puissance : Si a et b sont des entiers relatifs et a ≡ b [n], alors ak ≡ bk [n] pour tout entier k.
- Petit Théorème de Fermat : Si p est un nombre premier et a est un entier relatif non divisible par p, alors ap-1 ≡ 1 [p].
Critère de Divisibilité par 9
Un nombre entier est divisible par 9 si et seulement si la somme de ses chiffres est divisible par 9.
Démonstration :
Soit un nombre entier N.
N = 10nanan + 10n-1an-1+...+102a2+ 10a1 où ak sont ses chiffres.
10 ≡ 1 [9]
Donc pour tout entier k, on a : 10k ≡ 1 [9]
Donc N ≡ an + an-1 + ... + a0 [9]



