Sommaire : Fiches

01 - POO, Piles, Files, Listes, Dictionnaires
02 - Arbre
03 - Graphe
04 - SQL
05 - Routage
06 - Récursivité et Diviser pour régner
07 - Système sur Puce et Processus Système
08 - Modularité
09 - Tri par insertion, tri par selection
10 - Les congruences

01 - POO, Piles, Files, Listes, Dictionnaires

Fiche de Révision : POO, Piles, Files, Listes, Dictionnaires - Tle NSI

1. Interface, Implémentation, POO

Concepts clés :

class Voiture: # Classe structure qui permet de définir des objets qui encapsulent des données et des fonctions.
    def __init__(self, marque, modele, kilometrage):# Constructeur, et self fait référence à l'instance actuelle.
        self.marque = marque # Attribut
        self.modele = modele # Attribut
        self.kilometrage = kilometrage # Attribut interne de l'objet ou de l'instance
        
    def afficher_details(self): # Méthode
        print(f"Voiture {self.marque} {self.modele}, {self.kilometrage} km parcourus.")
        
    def conduire(self, km): # Méthode
        self.kilometrage += km

# Exemple
v1 = Voiture("Peugeot", "208", 10000) # Création d'une instance de la classe.
v1.afficher_details()
v1.conduire(150)
v1.afficher_details()

v2 = Voiture("Tesla", "Modèle 3", 60000) # Création d'une autre instance de la classe.
v2.afficher_details()
Voiture Peugeot 208, 10000 km parcourus.
Voiture Peugeot 208, 10150 km parcourus.
Voiture Tesla Modèle 3, 60000 km parcourus.

2. Piles, Files, Listes

Concepts clés :

# Exemple de pile en Python
pile = []
pile.append(10)
pile.append(20)
pile.append(30)
print(pile) # Affiche [10, 20, 30]
print(pile.pop())  # Retire 30
print(pile)        # Affiche [10, 20]
[10, 20, 30]
30
[10, 20]

# Exemple de file en Python
file = []
file.append(10)
file.append(20)
file.append(30)
print(file) # Affiche [10, 20,30]
print(file.pop(0))  # Retire 10
print(file)         # Affiche [20, 30]
[10, 20, 30]
10
[20, 30]

3. Dictionnaires

Concepts clés :

# Exemple de dictionnaire en Python
dictionnaire = {'a': 1, 'b': 2, 'c': 3}
print(dictionnaire['a'])  # Accès à la valeur associée à la clé 'a'
dictionnaire['d'] = 4    # Ajout d'une nouvelle clé-valeur
del dictionnaire['b']    # Suppression de la clé 'b'
print(dictionnaire)
1
{'a': 1, 'c': 3, 'd': 4}

# Exemple mettant en œuvre les trois types de boucle for sur un dictionnaire
dictionnaire = {'a': 1, 'b': 2, 'c': 3}

# Boucle sur les clés
print("Parcours des clés :")
for cle in dictionnaire:
    print(f"Clé : {cle}")

# Boucle sur les valeurs
print("\nParcours des valeurs :")
for valeur in dictionnaire.values():
    print(f"Valeur : {valeur}")

# Boucle sur les paires clé-valeur
print("\nParcours des paires clé-valeur :")
for cle, valeur in dictionnaire.items():
    print(f"Clé : {cle}, Valeur : {valeur}")

Retour au sommaire

02 - Arbre

Fiche de Révision : Les Arbres - Terminale NSI

Concepts de base sur les arbres

Un arbre est une structure de données hiérarchique constituée de nœuds reliés par des arêtes. Les arbres sont utilisés pour modéliser des relations de type parent-enfant.

Définitions :

Arbres binaires

Un arbre binaire est un arbre dans lequel chaque nœud peut avoir au plus deux enfants.

Un arbre binaire de recherche (ABR) est un arbre binaire avec les propriétés suivantes :

class Noeud:
    def __init__(self, valeur, gauche=None, droit=None):
        self.valeur = valeur
        self.gauche = gauche
        self.droit = droit

# Exemple d’arbre binaire
racine = Noeud(40, Noeud(20, Noeud(10), Noeud(30)), Noeud(60, Noeud(50), Noeud(70)))

# autre méthode pour implémenter l'arbre en initialisant chaque nœud étape par étape
n10 = Noeud(10)
n30 = Noeud(30)
n20 = Noeud(20, n10, n30)
n50 = Noeud(50)
n70 = Noeud(70)
n60 = Noeud(60, n50, n70)
racine = Noeud(40, n20, n60)

Définitions Métriques :

def taille_arbre(noeud):
    if noeud is None:
        return 0
    return 1 + taille_arbre(noeud.gauche) + taille_arbre(noeud.droit)

def hauteur_arbre(noeud):
    if noeud is None:
        return -1
    return 1 + max(hauteur_arbre(noeud.gauche), hauteur_arbre(noeud.droit))

print("Taille de l’arbre :", taille_arbre(racine))
print("Hauteur de l’arbre :", hauteur_arbre(racine))
Taille de l’arbre : 7
Hauteur de l’arbre : 2

Parcours des arbres

Types de parcours :

  1. Préfixe (préordre) : Racine → Gauche → Droite
  2. Infixe (inordre) : Gauche → Racine → Droite
  3. Suffixe (postordre) : Gauche → Droite → Racine
  4. Largeur d'abord : Niveau par niveau, de gauche à droite.
def parcours_prefixe(noeud):
    if noeud is not None:
        return [noeud.valeur] + parcours_prefixe(noeud.gauche) + parcours_prefixe(noeud.droit)
    else:
        return []

def parcours_infixe(noeud):
    if noeud is not None:
        return parcours_infixe(noeud.gauche) + [noeud.valeur] + parcours_infixe(noeud.droit)
    else:
        return []

def parcours_suffixe(noeud):
    if noeud is not None:
        return parcours_suffixe(noeud.gauche) + parcours_suffixe(noeud.droit) + [noeud.valeur]
    else:
        return []
    
# Résultats des parcours
print("Parcours préfixe :", parcours_prefixe(racine))
print("Parcours infixe  :", parcours_infixe(racine))
print("Parcours suffixe :", parcours_suffixe(racine))
Parcours préfixe : [40, 20, 10, 30, 60, 50, 70]
Parcours infixe  : [10, 20, 30, 40, 50, 60, 70]
Parcours suffixe : [10, 30, 20, 50, 70, 60, 40]

def parcours_largeur(racine):
    if not racine:
        return []
    
    file = [racine]
    resultat = []
    while file:
        noeud = file.pop(0)  # Récupère le premier élément de la file
        resultat.append(noeud.valeur)
        if noeud.gauche:
            file.append(noeud.gauche)
        if noeud.droit:
            file.append(noeud.droit)
    return resultat

# Exemple d'utilisation
print("Parcours largeur :",parcours_largeur(racine))
Parcours largeur : [40, 20, 60, 10, 30, 50, 70]

Arbres binaires de recherche : Recherche et insertion

Recherche dans un ABR :

def rechercher(noeud, valeur):
    if noeud is None:
        return False
    if noeud.valeur == valeur:
        return True
    if valeur < noeud.valeur:
        return rechercher(noeud.gauche, valeur)
    return rechercher(noeud.droit, valeur)

print("Recherche 30 :", rechercher(racine, 30))
print("Recherche 100 :", rechercher(racine, 100))
Recherche 30 : True
Recherche 100 : False

Insertion dans un ABR :

def inserer(noeud, valeur):
    if noeud is None:
        return Noeud(valeur)
    if valeur < noeud.valeur:
        noeud.gauche = inserer(noeud.gauche, valeur)
    else:
        noeud.droit = inserer(noeud.droit, valeur)
    return noeud

racine = inserer(racine, 35)
print("Recherche 35 après insertion :", rechercher(racine, 35))
Recherche 35 après insertion : True

Arbres équilibrés (AVL)

Les arbres AVL sont des arbres binaires de recherche auto-équilibrés qui maintiennent une hauteur logarithmique, garantissant des opérations efficaces.

Propriétés : Complexité temporelle de recherche

La recherche dans un arbre AVL est de complexité 𝑂(𝑙𝑜𝑔(𝑛)), où 𝑛 est le nombre de nœuds dans l'arbre.

Si un arbre binaire de recherche n'est pas équilibré (par exemple, une structure en ligne droite), la complexité de recherche peut se dégrader vers 𝑂(𝑛) dans le pire des cas.

Retour au sommaire

03 - Graphe

Fiche de Révision : Graphes - NSI Terminale

Concepts Essentiels des Graphes

Définitions

  1. Sommet : Un point dans le graphe (nœud).
  2. Arête : Une connexion entre deux sommets.
    Orientée : Elle a une direction.
    Non-orientée : Elle n'a pas de direction.
  3. Graphe pondéré : Les arêtes ont un poids (ou coût).
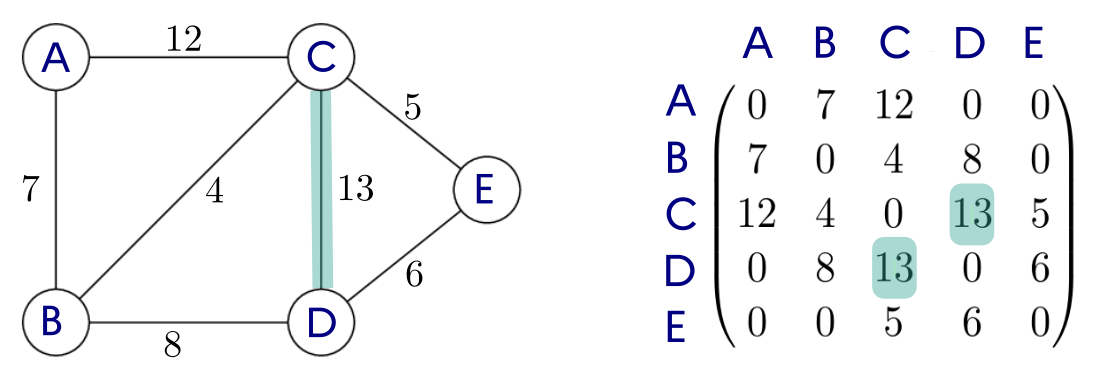
  4. Connexité : Un graphe est connexe si n'importe quelle paire de sommets peut toujours être reliée par une chaîne.
  5. Matrice d'adjacence : On représente les arêtes dans une matrice, c'est-à-dire un tableau à deux dimensions où on inscrit le poids en ligne i et colonne j de l'arête du sommets de rang i vers de rang j.
  6. Liste de successeurs : Liste des sommets accessibles depuis un sommet donné.
  7. Liste de prédécesseurs : Liste des sommets qui pointent vers un sommet donné.

Exemple

import numpy as np

class Graphe_Matrice_Adjacente:
    def __init__(self, matrice_adjacence, noms_sommets):
        self.matrice_adjacence = np.array(matrice_adjacence)
        self.noms_sommets = noms_sommets
        
    def liste_successeurs(self):
        liste_succ = {}
        n = len(self.matrice_adjacence)
        for i in range(n):
            successeurs = []
            for j in range(n):
                if self.matrice_adjacence[i][j]:
                    successeurs.append(self.noms_sommets[j])
            liste_succ[self.noms_sommets[i]] = successeurs
        return liste_succ


# Création d'un graphe avec la matrice d'adjacence donnée
matrice_adjacence = [[ 0, 7, 12,  0, 0],
                     [ 7, 0,  4,  8, 0],
                     [12, 4,  0, 13, 5],
                     [ 0, 8, 13,  0, 6],
                     [ 0, 0,  5,  6, 0] ]

noms_sommets = ['A', 'B', 'C', 'D', 'E']

# Instanciation de la classe Graphe_Matrice_Adjacente
graphe = Graphe_Matrice_Adjacente(matrice_adjacence, noms_sommets)
print("Liste des successeurs :",graphe.liste_successeurs())
Liste des successeurs : {'A': ['B', 'C'], 'B': ['A', 'C', 'D'], 'C': ['A', 'B', 'D', 'E'], 'D': ['B', 'C', 'E'], 'E': ['C', 'D']}

Algorithmes Importants sur les Graphes

DFS (Depth-First Search), traduit en français par "Parcours en profondeur d'abord", consiste à explorer un graphe en allant aussi loin que possible dans une branche avant de revenir en arrière pour explorer les voisins restants. Ce type de parcours ne tient pas compte des poids des arêtes : il se concentre sur le premier voisin non visité, qui à son tour procède de la même manière, jusqu'à ce qu'il n'y ait plus de voisins non explorés.

BFS (Breadth-First Search), traduit en français par "Parcours en largeur", explore tous les nœuds voisins d'un nœud avant de passer au niveau suivant. Ce type de parcours ignore également les poids des arêtes, mais il permet de trouver le plus court chemin entre deux nœuds en supposant que chaque arête a un poids égal à 1.

def DFS(graph,debut):
    result = []
    a_visite = [debut]
    while a_visite:
        noeux=a_visite.pop(0)
        if noeux not in result:
            result.append(noeux)
            a_visite = graph[noeux] + a_visite
    return result

def BFS(graph,debut):
    result = []
    a_visite = [debut]
    while a_visite:
        noeux = a_visite.pop(0)
        if noeux not in result:
            result.append(noeux)
            a_visite = a_visite +  graph[noeux]
    return result

# Exemple de graphe
graph_successeurs =  {'A': ['B', 'C', 'D'],
                      'B': ['A', 'E', 'F'],
                      'C': ['A', 'G', 'H'],
                      'D': ['A'],
                      'E': ['B'], 
                      'F': ['B'], 
                      'G': ['C', 'H'], 
                      'H': ['C', 'G']}

print("Ordre de visite DFS :", DFS(graph_successeurs, 'A'))
print("Ordre de visite BFS :", BFS(graph_successeurs, 'A'))
Ordre de visite DFS : ['A', 'B', 'E', 'F', 'C', 'G', 'H', 'D']
Ordre de visite BFS : ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']

Retour au sommaire

04 - SQL

Fiche de Révision : SQL - Terminale NSI

Partie 1 : Modèle Relationnel

Concepts principaux

  1. Relation : Une table dans une base de données.
  2. Attribut : Une colonne d'une table (propriété des données).
  3. Domaine : Ensemble de valeurs admissibles pour un attribut.
  4. Clé primaire : Identifiant unique d'une ligne dans une table.
  5. Clé étrangère : Attribut établissant un lien avec une clé primaire d'une autre table.

Exemple de schéma relationnel

AUTEURS(id : INT, nom : TEXT, prenom : TEXT, ann_naissance : INT, langue_ecriture : TEXT)

LIVRES(id : INT, titre : TEXT, #id_auteur : INT, ann_publi : INT, note : INT)

Les attributs soulignés sont des clés primaires, le # signifie que l'on a une clé étrangère.

Partie 2 : Requêtes SQL

1. Requêtes de sélection

2. Conditionner les résultats avec WHERE

3. Trier les résultats avec ORDER BY

4. Éviter les doublons avec DISTINCT

6. Compter

SELECT COUNT(*) 
FROM LIVRES 
WHERE note > 9;

7. Manipulations de données

Insérer des données

INSERT INTO LIVRES (id, titre, id_auteur, ann_publi, note)
VALUES (17, 'Hypérion', 11, 1989, 8);

Mettre à jour des données

UPDATE LIVRES
SET note = 10
WHERE titre = 'Dune';

Supprimer des données

DELETE FROM LIVRES
WHERE titre = 'Dune';

Attention : Sans WHERE, toutes les données seront supprimées :

DELETE FROM LIVRES;

Retour au sommaire

05 - Routage

Fiche BAC : Routage - Terminale NSI

1. Adresses IP et sous-réseaux

Concepts clés :

Exemple :

2. Tables de routage

Les routeurs permettent d'aiguiller les paquets entre les différents réseaux.

Une table de routage contient les informations nécessaires pour choisir le chemin :

Exemple : Table de routage du serveur R1

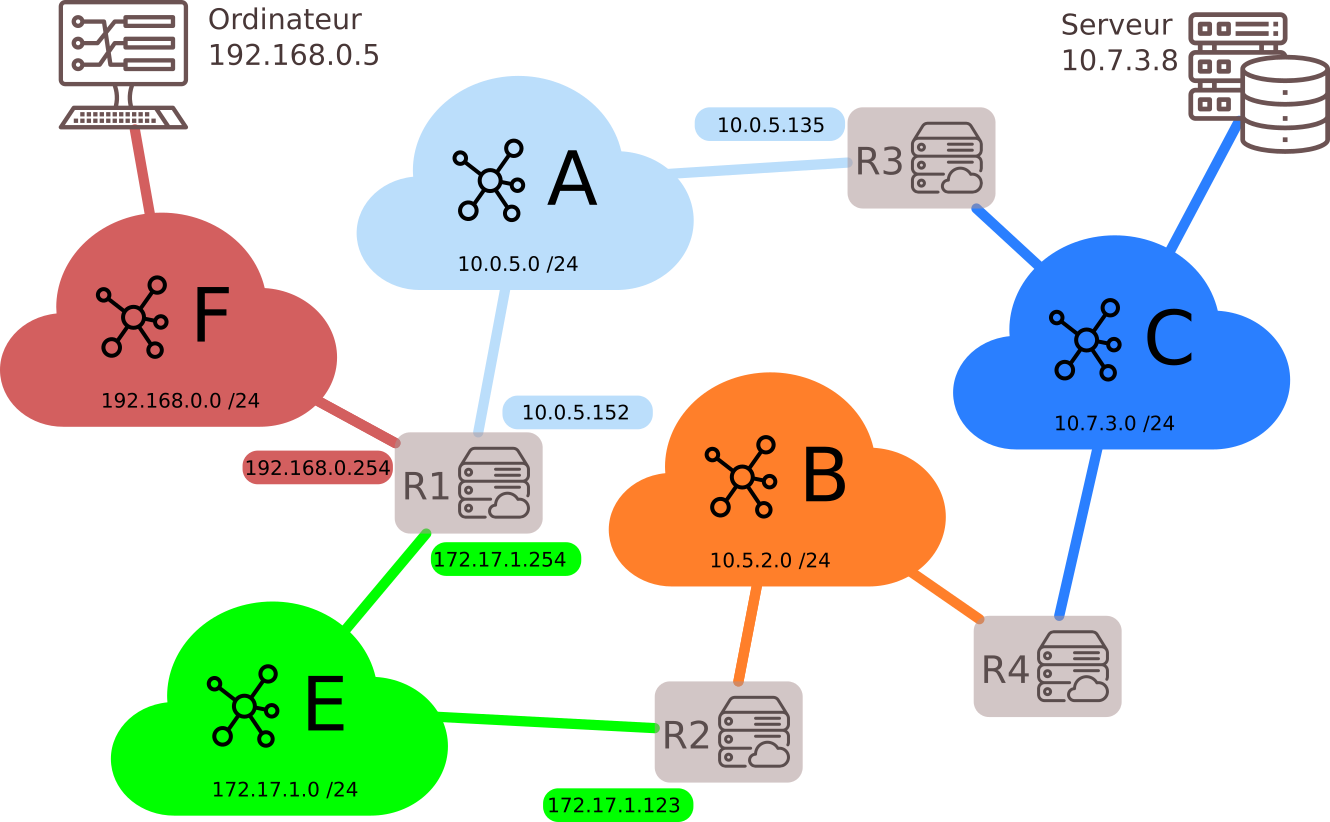
Destination Interface Passerelle
F 192.168.0.254
A 10.0.5.152
E 172.17.1.254
B 172.17.1.254 172.17.1.123
C 10.0.5.152 10.0.5.135

3. Protocole RIP (Routing Information Protocol)

Règles du RIP :

  1. Ajoute une route si elle est inconnue.
  2. Met à jour une route si une distance plus courte est trouvée.
  3. Ignore une route plus longue.
  4. Si un routeur est inactif pendant 3 minutes, la distance devient infinie (16).

4. Protocole OSPF (Open Shortest Path First)

Calcul du coût :

$coût = \frac{10^8}{débit}$ où $𝑑ébit$ est exprimé en bits/s

Rappel : 1 kbit = 1 000 bits ; 1Mbit = 1 000 kbits ; 1 Gbit = 1 000 Mbits

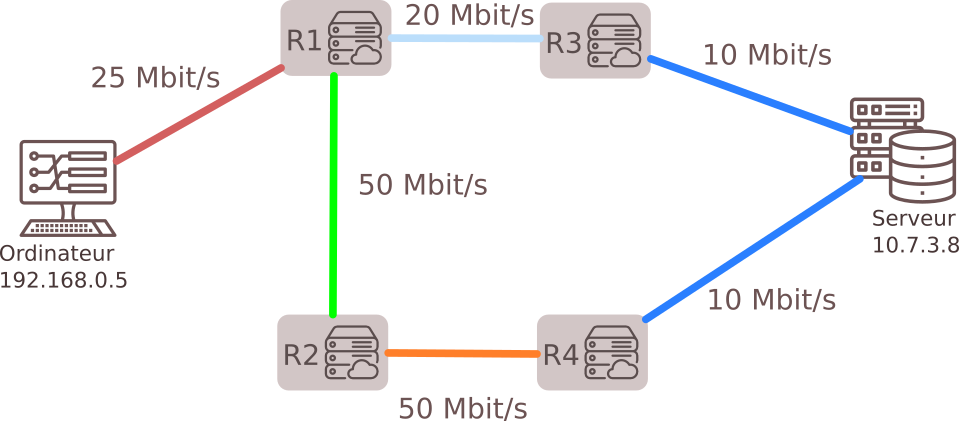
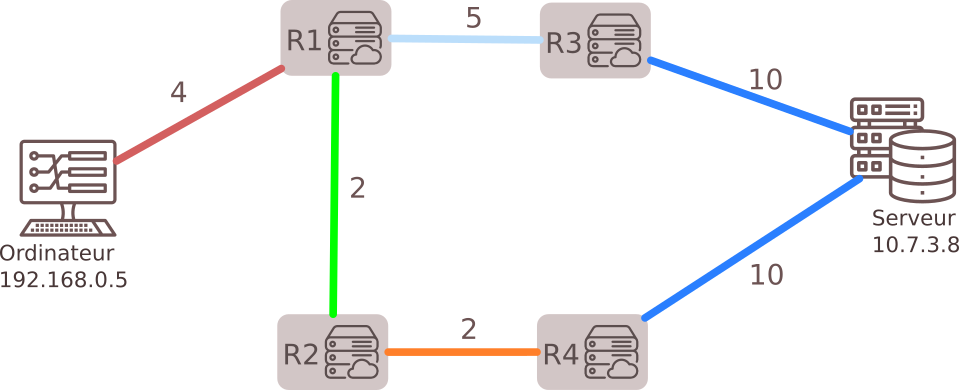
Le chemin le plus rapide pour aller de l'ordinateur 192.168.0.5 au serveur 10.7.3.8 est donc R1-R2-R4 avec un coût de 4 + 2 + 2 +10 = 18 , et non R1-R3 comme l'aurait indiqué le protocole RIP.

Retour au sommaire

06 - Récursivité et Diviser pour régner

Fiche de Révision : Récursivité et Diviser pour régner

1. La récursivité

Définition :

Une fonction récursive est une fonction qui s'appelle elle-même.

Structure d'une fonction récursive :

  1. Cas de base : Condition qui arrête la récursion.
  2. Appel récursif : Réduction du problème pour atteindre le cas de base.

Exemple : Calcul de la factorielle

def factorielle(n):
    if n == 0:  # Cas de base
        return 1
    else:
        return n * factorielle(n - 1)  # Appel récursif

print(factorielle(5))  # Résultat : 120
120

Points à vérifier pour la récursivité :

Attention :

Par défaut, Python autorise un maximum d'environ 1000 appels récursifs (ce nombre peut varier en fonction de la plateforme).

2. Diviser pour régner

Définition :

Un algorithme « Diviser pour régner » divise un problème en sous-problèmes, les résout de manière indépendante, puis combine les résultats.

Étapes principales :

  1. Diviser : Fractionner le problème en sous-problèmes plus petits.
  2. Régner : Résoudre récursivement chaque sous-problème.
  3. Combiner : Fusionner les solutions des sous-problèmes.

Exemple : Tri fusion (_Merge Sort_)

def tri_fusion(liste):
    if len(liste) <= 1:  # Cas de base
        return liste

    # Diviser
    milieu = len(liste) // 2
    gauche = tri_fusion(liste[:milieu])
    droite = tri_fusion(liste[milieu:])

    # Combiner
    return fusion(gauche, droite)

def fusion(gauche, droite):
    resultat = []
    while gauche and droite:
        if gauche[0] < droite[0]:
            resultat.append(gauche.pop(0))
        else:
            resultat.append(droite.pop(0))
    resultat = resultat + (gauche or droite)
    return resultat

# Exemple d'utilisation
print(tri_fusion([4, 3, 8, 2, 7, 1, 5]))  # Résultat : [1, 2, 3, 4, 5, 7, 8]
[1, 2, 3, 4, 5, 7, 8]

Retour au sommaire

07 - Système sur Puce et Processus Système

Fiche BAC : Système sur Puce et Processus/Système

1. Système sur Puce (SoC)

Définition :

Un Système sur Puce (System on Chip - SoC) intègre tous les composants nécessaires pour faire fonctionner un système informatique sur un seul circuit intégré.

Loi de Moore :

Exemple de SoC :

Processus :

Un processus est un programme en cours d'exécution, comprenant :

Threads :

Interblocage (Deadlock) :

Un interblocage se produit lorsque plusieurs processus attendent indéfiniment qu'une ressource détenue par un autre processus soit libérée.

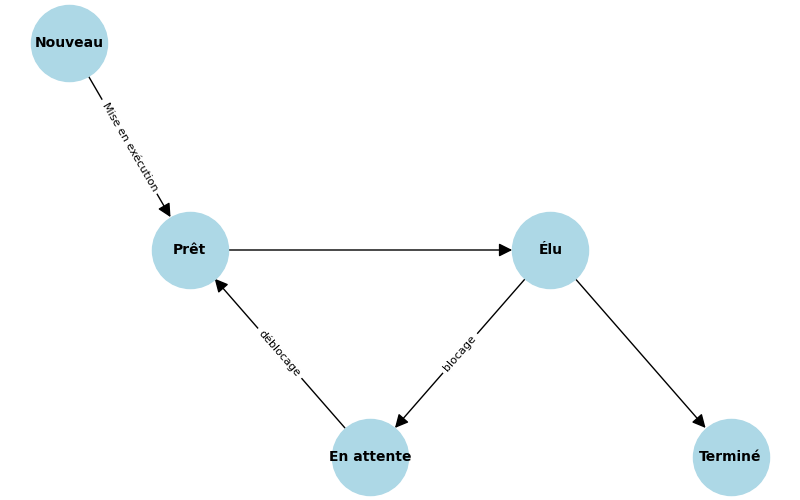
Conditions pour un interblocage :

  1. Exclusion mutuelle : Les ressources ne peuvent être utilisées que par un processus à la fois.
  2. Rétention et attente : Un processus retient une ressource tout en attendant d'autres ressources.
  3. Non-préemption : Les ressources ne peuvent pas être retirées de force.
  4. Attente circulaire : Les processus forment une chaîne circulaire d'attente de ressources.

Retour au sommaire

08 - Modularité

Fiche de Révision : Modularité

1. Qu'est-ce que la modularité ?

2. Modules Python

import math
dir(math)
['__doc__', '__loader__', '__name__', '__package__', '__spec__', 'acos', 'acosh', 'asin', 'asinh', 'atan', 'atan2', 'atanh', 'cbrt', 'ceil', 'comb', 'copysign', 'cos', 'cosh', 'degrees', 'dist', 'e', 'erf', 'erfc', 'exp', 'exp2', 'expm1', 'fabs', 'factorial', 'floor', 'fmod', 'frexp', 'fsum', 'gamma', 'gcd', 'hypot', 'inf', 'isclose', 'isfinite', 'isinf', 'isnan', 'isqrt', 'lcm', 'ldexp', 'lgamma', 'log', 'log10', 'log1p', 'log2', 'modf', 'nan', 'nextafter', 'perm', 'pi', 'pow', 'prod', 'radians', 'remainder', 'sin', 'sinh', 'sqrt', 'tan', 'tanh', 'tau', 'trunc', 'ulp']
help(math.sin)
Help on built-in function sin in module math:

sin(x, /)
    Return the sine of x (measured in radians).


print(math.sin.__doc__)
Return the sine of x (measured in radians).

3. Importations en Python

  1. import module : Accès à toutes les fonctions avec la notation pointée (module.fonction()).
  2. from module import fonction : Accès direct à la fonction (fonction()).
  3. *_`from module import _`** : Importe tout (déconseillé pour éviter les conflits de noms).
  4. Alias : Utilisez as pour renommer un module ou une fonction.
import math
math.sqrt(2)
1.4142135623730951
from math import sqrt
sqrt(2)
1.4142135623730951
from math import *
sqrt(2)
1.4142135623730951
from math import sqrt as racine_carree
racine_carree(2)
1.4142135623730951

4. Créer un module

Exemple :

def addition(a, b):
    """
    Retourne la somme de a et b.
       
    """
    return a + b
help(addition)
Help on function addition in module __main__:

addition(a, b)
    Retourne la somme de a et b.

Retour au sommaire

09 - Tri par insertion, tri par selection

Fiche de Révision : Tri par insertion, tri par selection

Tri par insertion

def tri_insertion(tab):
    n = len(tab)
    for i in range(1, n):
        valeur_insertion = tab[i]
        j = i
        while j > 0 and valeur_insertion < tab[j-1]:
            tab[j] = tab[j-1]
            j = j - 1
        tab[j] = valeur_insertion
    return tab

# Exemple d'utilisation
tab = [4, 3, 5, 1]
print("Tableau trié:",tri_insertion(tab) )
Tableau trié: [1, 3, 4, 5]

Tri par sélection

def tri_selection(tab):
    for i in range(len(tab)):
        min_i = i
        for j in range(i+1, len(tab)):
            if tab[min_i] > tab[j]:
                min_i = j
        tab[i], tab[min_i] = tab[min_i], tab[i]

# Exemple d'utilisation
tab = [12, 11, 13, 5, 6]
tri_selection(tab)
print("Tableau trié:", tab)
Tableau trié: [5, 6, 11, 12, 13]

Coût des algorithmes de tris par insertion, et par sélection

Propriété :
Les algorithmes de tris par insertion, par sélection ont un coût O($n^2$), où $n$ est la taille du tableau.

Cela signifie que le temps d'exécution augmente de manière quadratrique avec le nombre d'éléments dans le tableau.

Démonstration :
Comme chaque boucle interne peut prendre jusqu'à $n$ itérations et il y a $n$ boucles externes, cela donne un total de $n×n=n^2$ opérations dans le pire cas.

Retour au sommaire

10 - Les congruences

Les congruences


Théorème de Bézout :

Si a et b sont des entiers non nuls, alors il existe des entiers relatifs x et y, et un entier d tels que ax + by = d où d est le PGCD de a et b.

Algorithme d'Euclide (Classe de 3ième) ou PGCD de a et b

PDCD(a,b) = ?

1er cas : si b = 0
PDCD(a,b) = PDCD(a,0) = a

2ième Cas : si b > 0
Posons a = qb + r où q est le quotient et r est le reste de la division euclidienne de a par b.
d = PGCD(a,b) = PGCD(b,r) 

def pgcd(a, b):
    if b == 0:
        return a
    else:
        return pgcd(b, a % b)

# Exemple d'utilisation
a = 91
b = 77
print("Le PGCD de", a, "et", b, "est :", pgcd(a, b))
Le PGCD de 91 et 77 est : 7

Algorithme d'Euclide étendu ou comment trouver des coefficients x et y de Bezout et le PDCD de a et b

1er cas : si b = 0
d =a, x = 1, y = 0 est une solution de ax + by = d

2ième Cas : si b > 0
ax + by = d <=> (qb + r)x + by = d <=> b(qx + y) + rx = d <=> bx1 + ry1 = d avec x1 = qx + y et y1 = x <=> bx1 + ry1 = d avec x = y1 et y = x1 - qy1 

def euclide_etendu(a, b):
    if b == 0:
        return a, 1, 0
    else:
        pgcd, x1, y1 = euclide_etendu(b, a % b)
        x = y1
        y = x1 - (a // b) * y1
        return pgcd, x, y

# Exemple d'utilisation
a = 91
b = 77
pgcd, x, y = euclide_etendu(a, b)
print(f"Une solution de {a}x + {b}y = d est {a}({x}) + {b}({y}) = {pgcd}.")
Une solution de 91x + 77y = d est 91(-5) + 77(6) = 7.

Théorème de Gauss :

Si a, b et c sont des entiers non nuls.
Si a divise le produit bc et si a et b sont premiers entre eux alors a divise c.

Définition de la Congruence :

Soient a, b, n des entiers relatifs.
On dit que a est congruent à b modulo n, noté a≡b (mod n) ou a≡b[n], si n divise la différence a−b.

Propriétés des Propriétés de Congruence :

  1. Réflexivité : Pour tout entier relatif a, a ≡ a [n].
  2. Symétrie : Si a et b sont des entiers relatifs et a ≡ b [n], alors b ≡ a [n].
  3. Transitivité : Si a, b, et c sont des entiers relatifs et a ≡ b [n] et b ≡ c [n], alors a ≡ c [n].
  4. Addition : Si a, b, c, et d sont des entiers relatifs et a ≡ b [n] et c ≡ d [n], alors a + c ≡ b + d [n].
  5. Soustraction : Si a, b, c, et d sont des entiers relatifs et a ≡ b [n] et c ≡ d [n], alors a - c ≡ b - d [n].
  6. Multiplication : Si a, b, c, et d sont des entiers relatifs et a ≡ b [n] et c ≡ d [n], alors a * c ≡ b * d [n].
  7. Puissance : Si a et b sont des entiers relatifs et a ≡ b [n], alors ak ≡ bk [n] pour tout entier k.
  8. Petit Théorème de Fermat : Si p est un nombre premier et a est un entier relatif non divisible par p, alors ap-1 ≡ 1 [p].

Critère de Divisibilité par 9

Un nombre entier est divisible par 9 si et seulement si la somme de ses chiffres est divisible par 9.

Démonstration :

Soit un nombre entier N.
N = 10nanan + 10n-1an-1+...+102a2+ 10a1 où ak sont ses chiffres.

10 ≡ 1 [9]
Donc pour tout entier k, on a : 10k ≡ 1 [9]
Donc N ≡ an + an-1 + ... + a0 [9]

Retour au sommaire

↑ Haut de la page