Un dioptre est la séparation entre deux milieux transparents homogènes d'indices N1 et N2.

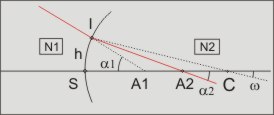On considère un dioptre sphérique de rayon R = SC Un rayon frappe le dioptre en I avec l'incidence i = α1 − ω L'angle de réfraction est r = ω − α2. la relation de Descartes donne : N1.sin i = N2.sin r

Lorsque le rayon lumineux passe d'un milieu moins réfringent vers un milieu plus réfringent (n1 < n2), il se rapproche de la normale, et lorsqu'il passe d'un milieu plus réfringent vers un milieu moins réfringent (n1 > n2), il s'écarte de la normale. Si l'angle d'incidence est trop grand il n'émerge pas: il y a réflexion totale. Dans le programme, les rayons réfléchis qui correspondent à cette situation ont été éliminés.

La relation de Descartes n'étant pas linéaire le dioptre sphérique n'est pas stigmatique dans le cas général.
Tout rayon passant par le centre C du dioptre n'est pas dévié : C est stigmatique.
La droite AC joignant le point source A au centre du dioptre est tracée en cyan.
On montre que deux autres points, les points d'Young-Weierstrass sont également stigmatiques.
Si on se place dans le cas de rayons peu inclinés sur l'axe il y a stigmatisme approché : on peut considérer que le point de convergence des rayons forme l'image du point objet.
Quand le dioptre est pratiquement stigmatique, le point "image" est situé sur la droite AC.
Quand le point objet est à l'infini, on dit que le point image est le foyer image Fi. Il est tel que SFi = fi = SC.N2 / (N2 − N1).
De même si le point image est à l'infini, le point objet est situé au foyer objet Fo tel que SFo = fo = SC.N1 / (N1 − N2).
Consulter cette page pour l'étude des relations de conjugaison.

Utilisation
Faire varier courbure et indices.
Chercher quand le le dioptre est convergent.
Chercher les foyers objet et image du dioptre.(Ils sont de part et d'autre du dioptre, mais ne sont pas équidistants du sommet). Comparer vos résultats avec ceux du programme sur les relations de conjugaison.
Vérifier le stigmatisme du centre et des points de Weierstrass.

Examiner le cas du dioptre plan (c = 0)